DAA - इष्टतम लागत द्विआधारी खोज पेड़
एक बाइनरी सर्च ट्री (BST) एक ऐसा पेड़ है जहां आंतरिक नोड्स में मुख्य मूल्य संग्रहीत होते हैं। बाहरी नोड्स नल नोड्स हैं। कुंजी को लेक्सिकोग्राफ़िक रूप से क्रमबद्ध किया गया है, अर्थात प्रत्येक आंतरिक नोड के लिए बाएं उप-ट्री की सभी कुंजियाँ नोड की कुंजियों से कम हैं, और दाएँ उप-ट्री की सभी कुंजियाँ अधिक हैं।
जब हम चाबियों में से हर एक को खोजने की आवृत्ति जानते हैं, तो पेड़ में प्रत्येक नोड तक पहुंचने की अपेक्षित लागत की गणना करना काफी आसान है। एक इष्टतम बाइनरी सर्च ट्री एक BST है, जिसमें प्रत्येक नोड का पता लगाने की न्यूनतम अपेक्षित लागत होती है
BST में एक तत्व का खोज समय है O(n), जबकि एक संतुलित-बीएसटी खोज समय है O(log n)। ऑप्टिमल कॉस्ट बाइनरी सर्च ट्री में फिर से खोज के समय में सुधार किया जा सकता है, सबसे अधिक बार उपयोग किए जाने वाले डेटा को रूट में और रूट तत्व के करीब रखते हुए, पत्तियों के पास और पत्तियों में कम से कम अक्सर उपयोग किए गए डेटा को रखते हुए।
यहां, इष्टतम बाइनरी सर्च ट्री एल्गोरिथम प्रस्तुत किया गया है। पहले, हम प्रदान किए गए सेट से एक BST बनाते हैंn अलग-अलग चाबियों की संख्या < k1, k2, k3, ... kn >। यहाँ हम मानते हैं, एक कुंजी तक पहुँचने की संभावनाKi है pi। कुछ डमी कुंजी (d0, d1, d2, ... dn) को जोड़ा जाता है क्योंकि कुछ खोज उन मानों के लिए किए जा सकते हैं जो कुंजी सेट में मौजूद नहीं हैं K। हम मानते हैं, प्रत्येक डमी कुंजी के लिएdi पहुंच की संभावना है qi।
Optimal-Binary-Search-Tree(p, q, n)
e[1…n + 1, 0…n],
w[1…n + 1, 0…n],
root[1…n + 1, 0…n]
for i = 1 to n + 1 do
e[i, i - 1] := qi - 1
w[i, i - 1] := qi - 1
for l = 1 to n do
for i = 1 to n – l + 1 do
j = i + l – 1 e[i, j] := ∞
w[i, i] := w[i, i -1] + pj + qj
for r = i to j do
t := e[i, r - 1] + e[r + 1, j] + w[i, j]
if t < e[i, j]
e[i, j] := t
root[i, j] := r
return e and rootविश्लेषण
एल्गोरिथ्म की आवश्यकता है O (n3) समय, तीन नेस्टेड के बाद से forछोरों का उपयोग किया जाता है। इनमें से प्रत्येक लूप सबसे अधिक लेता हैn मान।
उदाहरण
निम्नलिखित पेड़ को ध्यान में रखते हुए, लागत 2.80 है, हालांकि यह एक इष्टतम परिणाम नहीं है।
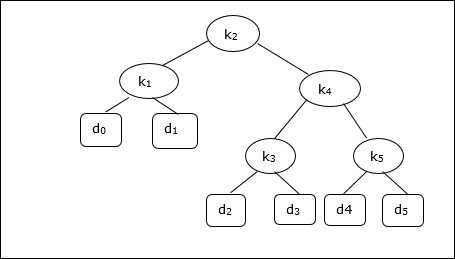
| नोड | गहराई | संभावना | योगदान |
|---|---|---|---|
| k १ | 1 | 0.15 | 0.30 |
| के २ | 0 | 0.10 | 0.10 |
| के ३ | 2 | 0.05 | 0.15 |
| के ४ | 1 | 0.10 | 0.20 |
| के ५ | 2 | 0.20 | 0.60 |
| घ ० | 2 | 0.05 | 0.15 |
| घ १ | 2 | 0.10 | 0.30 |
| घ २ | 3 | 0.05 | 0.20 |
| घ ३ | 3 | 0.05 | 0.20 |
| घ ४ | 3 | 0.05 | 0.20 |
| घ ५ | 3 | 0.10 | 0.40 |
| Total | 2.80 |
एक इष्टतम समाधान प्राप्त करने के लिए, इस अध्याय में चर्चा किए गए एल्गोरिथ्म का उपयोग करके, निम्न तालिकाओं को उत्पन्न किया जाता है।
निम्नलिखित तालिकाओं में, स्तंभ सूचकांक है i और पंक्ति सूचकांक है j।
| इ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 2.75 | 2.00 | 1.30 | 0.90 | 0.50 | 0.10 |
| 4 | 1.75 | 1.20 | 0.60 | 0.30 | 0.05 | |
| 3 | 1.25 | 0.70 | 0.25 | 0.05 | ||
| 2 | 0.90 | 0.40 | 0.05 | |||
| 1 | 0.45 | 0.10 | ||||
| 0 | 0.05 |
| w | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 1.00 | 0.80 | 0.60 | 0.50 | 0.35 | 0.10 |
| 4 | 0.70 | 0.50 | 0.30 | 0.20 | 0.05 | |
| 3 | 0.55 | 0.35 | 0.15 | 0.05 | ||
| 2 | 0.45 | 0.25 | 0.05 | |||
| 1 | 0.30 | 0.10 | ||||
| 0 | 0.05 |
| जड़ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 2 | 4 | 5 | 5 | 5 |
| 4 | 2 | 2 | 4 | 4 | |
| 3 | 2 | 2 | 3 | ||
| 2 | 1 | 2 | |||
| 1 | 1 |
इन तालिकाओं से, इष्टतम पेड़ बनाया जा सकता है।