DAA - मल्टीस्टेज ग्राफ
एक मल्टीस्टेज ग्राफ G = (V, E) एक ऐसा निर्देशित ग्राफ है, जिसमें वर्टिकल को विभाजित किया गया है k (कहाँ पे k > 1) असंबद्ध सबसेट की संख्या S = {s1,s2,…,sk}ऐसा किनारा (u, v) E में है, तो u v s i और v (s 1 + 1 विभाजन में कुछ सबसेट के लिए और |s1| = |sk| = 1।
शीर्षासन s Є s1 कहा जाता है source और शीर्ष t Є sk कहा जाता है sink।
Gआमतौर पर इसे भारित ग्राफ माना जाता है। इस ग्राफ में, एक किनारे की लागत (i, j) को c (i, j) द्वारा दर्शाया गया है । इसलिए, स्रोत से पथ की लागतs डूबना t इस मार्ग में प्रत्येक किनारों की लागत का योग है।
मल्टीस्टेज ग्राफ समस्या स्रोत से न्यूनतम लागत के साथ रास्ता ढूंढ रही है s डूबना t।
उदाहरण
मल्टीस्टेज ग्राफ की अवधारणा को समझने के लिए निम्नलिखित उदाहरण पर विचार करें।
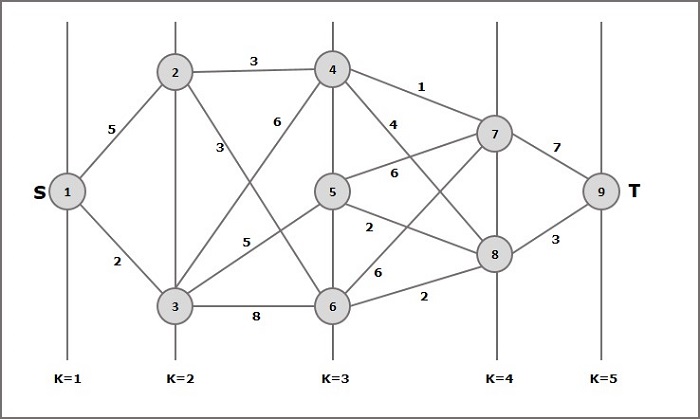
सूत्र के अनुसार, हमें लागत की गणना करनी होगी (i, j) निम्नलिखित चरणों का उपयोग कर
चरण -1: लागत (K-2, j)
इस चरण में, तीन नोड्स (नोड 4, 5. 6) के रूप में चुने गए हैं j। इसलिए, इस कदम पर न्यूनतम लागत चुनने के लिए हमारे पास तीन विकल्प हैं।
लागत (3, 4) = मिनट {c (4, 7) + लागत (7, 9), सी (4, 8) + लागत (8, 9)} = 7
लागत (3, 5) = मिनट {c (5, 7) + लागत (7, 9), सी (5, 8) + लागत (8, 9)} = 5
लागत (3, 6) = मिनट {c (6, 7) + लागत (7, 9), सी (6, 8) + लागत (8, 9)} = 5
चरण -2: लागत (K-3, j)
दो नोड्स को j के रूप में चुना जाता है क्योंकि स्टेज k - 3 = 2 पर दो नोड्स होते हैं, 2 और 3. तो, मान i = 2 और j = 2 और 3।
लागत (2, 2) = मिनट {c (2, 4) + लागत (4, 8) + लागत (8, 9), सी (2, 6) +
लागत (6, 8) + लागत (8, 9)} = 8
लागत (2, 3) = {c (3, 4) + लागत (4, 8) + लागत (8, 9), सी (3, 5) + लागत (5, 8) + लागत (8, 9) c (3, 6) + लागत (6, 8) + लागत (8, 9)} = 10
चरण -3: लागत (K-4, j)
लागत (1, 1) = {c (1, 2) + लागत (2, 6) + लागत (6, 8) + लागत (8, 9), सी (1, 3) + लागत (3, 5) + लागत (5, 8) + लागत (8, 9))} = 12
c (1, 3) + लागत (3, 6) + लागत (6, 8 + लागत (8, 9))}} 13
इसलिए, न्यूनतम लागत वाला मार्ग है 1→ 3→ 5→ 8→ 9।