डीएए - स्पैनिंग ट्री
ए spanning tree एक अप्रत्यक्ष ग्राफ़ का एक सबसेट है जिसमें सभी किनारों को न्यूनतम संख्या में किनारों से जोड़ा गया है।
यदि सभी कोने एक ग्राफ में जुड़े हुए हैं, तो कम से कम एक फैले हुए पेड़ मौजूद हैं। एक ग्राफ में, एक से अधिक फैले हुए वृक्ष मौजूद हो सकते हैं।
गुण
- एक फैले हुए वृक्ष का कोई चक्र नहीं होता है।
- किसी भी शीर्ष पर किसी अन्य शीर्ष से पहुंचा जा सकता है।
उदाहरण
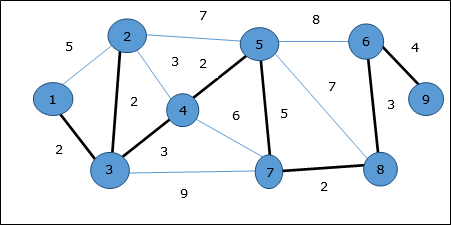
निम्नलिखित ग्राफ में, हाइलाइट किए गए किनारे एक फैले हुए पेड़ का निर्माण करते हैं।
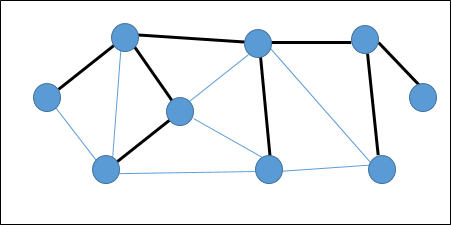
न्यूनतम फैलाव वाला पेड़
ए Minimum Spanning Tree (MST)एक कनेक्टेड वेटेड अप्रत्यक्ष ग्राफ के किनारों का एक सबसेट है, जो न्यूनतम संभव कुल बढ़त वजन के साथ सभी कोने जोड़ता है। एक एमएसटी प्राप्त करने के लिए, प्राइम के एल्गोरिथ्म या क्रुस्कल के एल्गोरिथ्म का उपयोग किया जा सकता है। इसलिए, हम इस अध्याय में प्राइम के एल्गोरिथ्म पर चर्चा करेंगे।
जैसा कि हमने चर्चा की है, एक ग्राफ में एक से अधिक फैले हुए पेड़ हो सकते हैं। अगर वहाँn वर्टिस की संख्या, फैले हुए पेड़ होना चाहिए n - 1किनारों की संख्या। इस संदर्भ में, यदि ग्राफ़ का प्रत्येक किनारा एक भार के साथ जुड़ा हुआ है और एक से अधिक फैले हुए वृक्ष मौजूद हैं, तो हमें ग्राफ़ के न्यूनतम फैले हुए पेड़ को खोजने की आवश्यकता है।
इसके अलावा, अगर कोई डुप्लिकेट वेटेड किनारों मौजूद हैं, तो ग्राफ में कई न्यूनतम फैले हुए पेड़ हो सकते हैं।
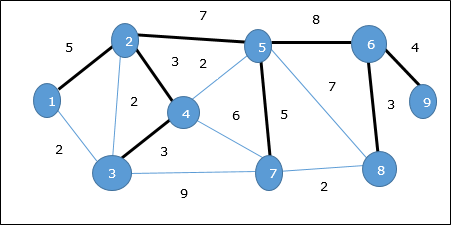
उपरोक्त ग्राफ में, हमने एक फैले हुए पेड़ को दिखाया है, हालांकि यह न्यूनतम फैले हुए पेड़ नहीं है। इस फैले हुए पेड़ की लागत (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38 है।
न्यूनतम फैले हुए वृक्ष को खोजने के लिए हम प्राइम के एल्गोरिथ्म का उपयोग करेंगे।
प्राइम का एल्गोरिथम
प्राइम का एल्गोरिथ्म न्यूनतम फैले हुए पेड़ को खोजने के लिए एक लालची दृष्टिकोण है। इस एल्गोरिथ्म में, एक एमएसटी बनाने के लिए हम एक अनियंत्रित शीर्ष से शुरू कर सकते हैं।
Algorithm: MST-Prim’s (G, w, r)
for each u є G.V
u.key = ∞
u.∏ = NIL
r.key = 0
Q = G.V
while Q ≠ Ф
u = Extract-Min (Q)
for each v є G.adj[u]
if each v є Q and w(u, v) < v.key
v.∏ = u
v.key = w(u, v)फ़ंक्शन एक्सट्रैक्ट-मिन न्यूनतम बढ़त लागत के साथ वर्टेक्स लौटाता है। यह फ़ंक्शन मिन-हीप पर काम करता है।
उदाहरण
प्राइम के एल्गोरिथ्म का उपयोग करते हुए, हम किसी भी शीर्ष से शुरू कर सकते हैं, हमें शीर्ष से शुरू करते हैं 1।
शिखर 3 वर्टेक्स से जुड़ा है 1 न्यूनतम बढ़त लागत के साथ, इसलिए बढ़त (1, 2) फैले पेड़ में जोड़ा जाता है।
अगला, किनारा (2, 3) माना जाता है कि यह किनारों के बीच न्यूनतम है {(1, 2), (2, 3), (3, 4), (3, 7)}।
अगले चरण में, हमें बढ़त मिलती है (3, 4) तथा (2, 4)न्यूनतम लागत के साथ। एज(3, 4) यादृच्छिक पर चुना गया है।
इसी तरह से, किनारों (4, 5), (5, 7), (7, 8), (6, 8) तथा (6, 9)चुने गए हैं। के रूप में सभी कोने का दौरा कर रहे हैं, अब एल्गोरिथ्म बंद हो जाता है।
फैले हुए वृक्ष की लागत (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23 है। इस ग्राफ में कोई अधिक फैलाव वाला वृक्ष नहीं है, जिसकी लागत कम है 23।