उचित अंशों की मॉडलिंग गुणन

आइए एक क्षेत्र मॉडल का उपयोग अंशों को गुणा करने के लिए करें। क्षेत्र मॉडल हमें एक अच्छी तस्वीर देता है जो तब होता है जब हम दो अंशों को गुणा करते हैं। समस्या को हम दो आयामों में देखते हैं। हम एक अंश का उपयोग करके ऊंचाई का प्रतिनिधित्व करते हैं और दूसरे अंश का उपयोग करके चौड़ाई। गणित में इस तरह के कनेक्शन को देखना महत्वपूर्ण है।

एक क्षेत्र मॉडल $ \ frac {1} {3} $ × $ \ frac {1} {3} $ का उपयोग करके अंशों को गुणा करें

उपाय

Step 1:

इस समस्या में, हम पता लगाना चाहते हैं $ \ frac {1} {3} $ के $ \ frac {1} {3} $

Step 2:

पहले हम एक आयत की ऊँचाई को 3 बराबर भागों में विभाजित करते हैं।

Step 3:

हम $ \ frac {1} {3} $ का प्रतिनिधित्व करने के लिए एक भाग को शेड करते हैं

Step 4:

आगे हम चौड़ाई को 3 बराबर भागों में बांटते हैं और 1 भाग को छायादार बनाते हैं इसे $ frac {1} {3} $ बनाते हैं

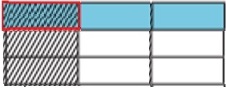
Step 5:

अब हम उत्पाद का पता लगा सकते हैं। वह भाग जहाँ शेडिंग ओवरलैप्स अंश का प्रतिनिधित्व करता है। भागों की कुल संख्या हर का प्रतिनिधित्व करती है। कुल 9 भाग हैं और 1 भाग ओवरलैप हैं।

Step 6:

तो, उत्पाद $ \ frac {1} {9} $ है ।

$ \ frac {1} {3} $ × $ \ frac {1} {3} $ = $ \ frac {1} {9} $

एक क्षेत्र मॉडल $ \ frac {2} {3} $ × $ \ frac {1} {3} $ का उपयोग करके अंशों को गुणा करें

उपाय

Step 1:

इस समस्या में, हम पता लगाना चाहते हैं $ \ frac {2} {3} $ के $ \ frac {1} {3} $

Step 2:

पहले हम एक आयत की ऊँचाई को 3 बराबर भागों में विभाजित करते हैं।

Step 3:

हम $ \ frac {1} {3} $ का प्रतिनिधित्व करने के लिए एक भाग को शेड करते हैं

Step 4:

अगला हम चौड़ाई को 3 बराबर भागों में विभाजित करते हैं और इसे $ \ frac {2} {3} $ बनाने के लिए 2 भागों को शेड करते हैं

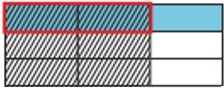
Step 5:

अब हम उत्पाद का पता लगा सकते हैं। वह भाग जहाँ शेडिंग ओवरलैप्स अंश का प्रतिनिधित्व करता है। भागों की कुल संख्या हर का प्रतिनिधित्व करती है। कुल भागों के 9 और ओवरलैप्स के 2 भाग हैं।

Step 6:

तो, उत्पाद $ \ frac {2} {9} $ है ।

$ \ frac {2} {3} $ × $ \ frac {1} {3} $ = $ \ frac {2} {9} $

एक क्षेत्र मॉडल $ \ frac {1} {2} $ × $ \ frac {1} {3} $ का उपयोग करके अंशों को गुणा करें

उपाय

Step 1:

इस समस्या में, हम पता लगाना चाहते हैं $ \ frac {1} {2} $ के $ \ frac {1} {3} $

Step 2:

पहले हम एक आयत की ऊँचाई को 3 बराबर भागों में विभाजित करते हैं।

Step 3:

हम $ \ frac {1} {3} $ का प्रतिनिधित्व करने के लिए एक भाग को शेड करते हैं

Step 4:

आगे हम चौड़ाई को 2 बराबर भागों में बांटते हैं और 1 भाग छायांकित करते हैं ताकि इसे $ frac {1} {2} $ बनाया जा सके

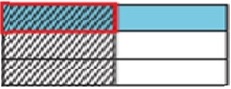
Step 5:

अब हम उत्पाद का पता लगा सकते हैं। वह भाग जहाँ शेडिंग ओवरलैप्स अंश का प्रतिनिधित्व करता है। भागों की कुल संख्या हर का प्रतिनिधित्व करती है। कुल 6 भाग हैं और 1 भाग ओवरलैप है।

Step 6:

तो, उत्पाद $ \ frac {1} {6} $ है ।

$ \ frac {1} {2} $ × $ \ frac {1} {3} $ = $ \ frac {1} {6} $