Teori Resonansi Adaptif
Jaringan ini dikembangkan oleh Stephen Grossberg dan Gail Carpenter pada tahun 1987. Berbasis kompetisi dan menggunakan model pembelajaran tanpa pengawasan. Jaringan Adaptive Resonance Theory (ART), seperti namanya, selalu terbuka untuk pembelajaran baru (adaptif) tanpa kehilangan pola lama (resonansi). Pada dasarnya, jaringan ART adalah pengklasifikasi vektor yang menerima vektor input dan mengklasifikasikannya ke dalam salah satu kategori tergantung dari pola tersimpan mana yang paling mirip.
Kepala Operasi
Operasi utama klasifikasi ART dapat dibagi menjadi beberapa fase berikut -
Recognition phase- Vektor masukan dibandingkan dengan klasifikasi yang disajikan pada setiap node pada lapisan keluaran. Keluaran neuron menjadi "1" jika paling cocok dengan klasifikasi yang diterapkan, jika tidak, menjadi "0".
Comparison phase- Pada tahap ini dilakukan perbandingan antara vektor masukan dengan vektor lapisan pembanding. Syarat untuk reset adalah bahwa derajat kesamaan akan lebih kecil dari parameter kewaspadaan.
Search phase- Pada fase ini, jaringan akan mencari reset serta kecocokan yang dilakukan pada fase di atas. Oleh karena itu, jika tidak ada pengaturan ulang dan kecocokan cukup baik, maka klasifikasi selesai. Jika tidak, proses akan diulang dan pola tersimpan lainnya harus dikirim untuk menemukan kecocokan yang benar.
ART1
Ini adalah jenis ART, yang dirancang untuk mengelompokkan vektor biner. Kita bisa memahami hal ini dengan arsitekturnya.
Arsitektur ART1
Ini terdiri dari dua unit berikut -
Computational Unit - Ini terdiri dari berikut -
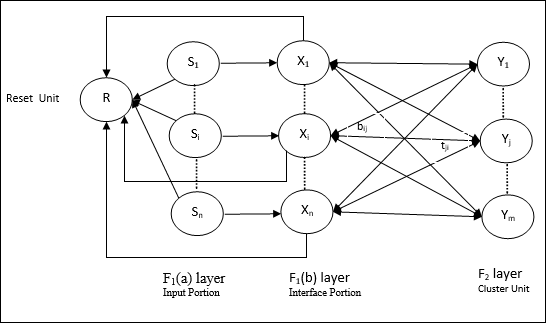
Input unit (F1 layer) - Ini selanjutnya memiliki dua bagian berikut -
F1(a) layer (Input portion)- Dalam ART1, tidak akan ada pemrosesan dalam bagian ini daripada hanya memiliki vektor input. Ini terhubung ke lapisan F 1 (b) (bagian antarmuka).
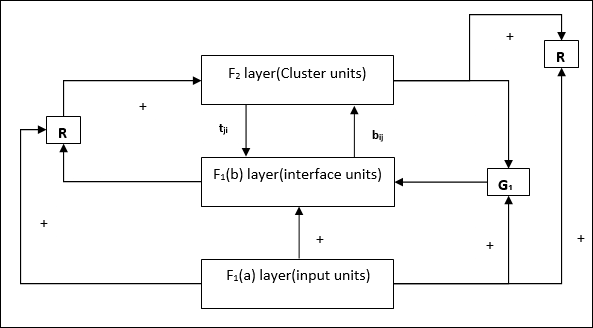
F1(b) layer (Interface portion)- Bagian ini menggabungkan sinyal dari bagian masukan dengan yang ada di lapisan F 2 . Lapisan F 1 (b) dihubungkan ke lapisan F 2 melalui bobot bottom upbijdan lapisan F 2 dihubungkan ke lapisan F 1 (b) melalui pemberat top downtji.
Cluster Unit (F2 layer)- Ini adalah lapisan kompetitif. Unit yang memiliki masukan bersih terbesar dipilih untuk mempelajari pola masukan. Aktivasi semua unit cluster lainnya disetel ke 0.
Reset Mechanism- Kerja mekanisme ini didasarkan pada kemiripan antara bobot top-down dan vektor input. Nah, jika derajat kemiripan ini lebih kecil dari parameter kewaspadaan, maka cluster tidak diperbolehkan mempelajari polanya dan akan terjadi istirahat.
Supplement Unit - Sebenarnya masalah dengan mekanisme Reset adalah lapisannya F2harus dihambat dalam kondisi tertentu dan juga harus tersedia saat pembelajaran terjadi. Itulah mengapa dua unit tambahan yaitu,G1 dan G2 ditambahkan bersama dengan unit reset, R. Mereka disebutgain control units. Unit ini menerima dan mengirim sinyal ke unit lain yang ada di jaringan.‘+’ menunjukkan sinyal rangsang, sementara ‘−’ menunjukkan sinyal penghambatan.
Parameter yang Digunakan
Parameter berikut digunakan -
n - Jumlah komponen dalam vektor masukan
m - Jumlah cluster maksimal yang bisa dibentuk
bij- Bobot dari lapisan F 1 (b) sampai F 2 , yaitu bobot bottom-up
tji- Bobot dari lapisan F 2 sampai F 1 (b), yaitu bobot top-down
ρ - Parameter kewaspadaan
||x|| - Norma vektor x
Algoritma
Step 1 - Inisialisasi kecepatan pembelajaran, parameter kewaspadaan, dan bobot sebagai berikut -
$$ \ alpha \:> \: 1 \: \: dan \: \: 0 \: <\ rho \: \ leq \: 1 $$
$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: dan \: \: t_ {ij} (0) \: = \: 1 $$
Step 2 - Lanjutkan langkah 3-9, jika kondisi penghentian tidak benar.
Step 3 - Lanjutkan langkah 4-6 untuk setiap input pelatihan.
Step 4- Atur aktivasi semua unit F 1 (a) dan F 1 sebagai berikut
F2 = 0 and F1(a) = input vectors
Step 5- Sinyal input dari layer F 1 (a) ke F 1 (b) harus dikirim seperti
$$ s_ {i} \: = \: x_ {i} $$
Step 6- Untuk setiap node F 2 yang terhambat
$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ kondisinya adalah yj ≠ -1
Step 7 - Lakukan langkah 8-10, jika reset benar.
Step 8 - Temukan J untuk yJ ≥ yj untuk semua node j
Step 9- Sekali lagi hitung aktivasi pada F 1 (b) sebagai berikut
$$ x_ {i} \: = \: sitJi $$
Step 10 - Sekarang, setelah menghitung norma vektor x dan vektor s, kita perlu memeriksa kondisi reset sebagai berikut -
Jika ||x||/ ||s|| <parameter kewaspadaan ρ, Kemudian hentikan node J dan lanjutkan ke langkah 7
Lain Jika ||x||/ ||s|| ≥ parameter kewaspadaan ρ, lalu lanjutkan lebih jauh.
Step 11 - Pembaruan bobot untuk node J dapat dilakukan sebagai berikut -
$$ b_ {ij} (baru) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$
$$ t_ {ij} (baru) \: = \: x_ {i} $$
Step 12 - Kondisi berhenti untuk algoritma harus diperiksa dan mungkin sebagai berikut -
- Tidak ada perubahan berat badan.
- Reset tidak dilakukan untuk unit.
- Jumlah periode maksimum tercapai.