Jaringan Saraf Tiruan - Jaringan Hopfield
Jaringan saraf hopfield ditemukan oleh Dr. John J. Hopfield pada tahun 1982. Ini terdiri dari satu lapisan yang berisi satu atau lebih neuron berulang yang terhubung sepenuhnya. Jaringan Hopfield biasanya digunakan untuk asosiasi otomatis dan tugas pengoptimalan.
Jaringan Hopfield Diskrit
Jaringan Hopfield yang beroperasi secara diskrit atau dengan kata lain pola masukan dan keluarannya adalah vektor diskrit, yang dapat berbentuk biner (0,1) atau bipolar (+1, -1). Jaringan memiliki bobot simetris tanpa koneksi mandiri, misalnya,wij = wji dan wii = 0.
Arsitektur
Berikut adalah beberapa poin penting yang perlu diingat tentang jaringan Hopfield yang terpisah -
Model ini terdiri dari neuron dengan satu keluaran pembalik dan satu keluaran non-pembalik.
Keluaran setiap neuron harus merupakan masukan dari neuron lain tetapi bukan masukan diri.
Berat / kekuatan koneksi diwakili oleh wij.
Koneksi bisa menjadi rangsang sekaligus penghambatan. Ini akan menjadi rangsang, jika keluaran neuron sama dengan masukan, jika tidak penghambatan.
Bobot harus simetris, yaitu wij = wji
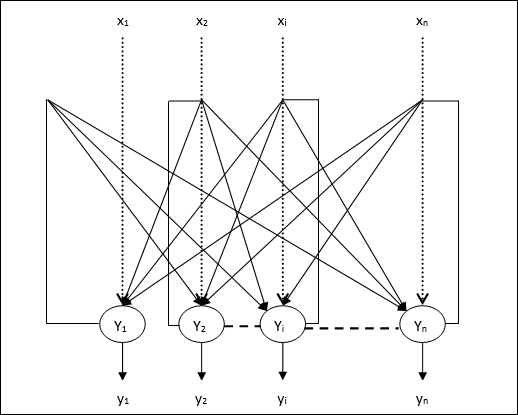
Keluaran dari Y1 pergi ke Y2, Yi dan Yn berbobot w12, w1i dan w1nmasing-masing. Demikian pula, busur lain memiliki bobot pada mereka.
Algoritma Pelatihan
Selama pelatihan jaringan Hopfield diskrit, bobot akan diperbarui. Seperti yang kita ketahui bahwa kita dapat memiliki vektor masukan biner dan juga vektor masukan bipolar. Karenanya, dalam kedua kasus, pembaruan bobot dapat dilakukan dengan relasi berikut
Case 1 - Pola masukan biner
Untuk satu set pola biner s(p), p = 1 to P
Sini, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Matriks Bobot diberikan oleh
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: untuk \: i \: \ neq \: j $$
Case 2 - Pola masukan bipolar
Untuk satu set pola biner s(p), p = 1 to P
Sini, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Matriks Bobot diberikan oleh
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: untuk \ : i \: \ neq \: j $$
Menguji Algoritma
Step 1 - Inisialisasi bobot, yang diperoleh dari algoritma pelatihan dengan menggunakan prinsip Hebbian.
Step 2 - Lakukan langkah 3-9, jika aktivasi jaringan tidak digabungkan.
Step 3 - Untuk setiap vektor masukan X, lakukan langkah 4-8.
Step 4 - Buat aktivasi awal jaringan sama dengan vektor input eksternal X sebagai berikut -
$$ y_ {i} \: = \: x_ {i} \: \: \: untuk \: i \: = \: 1 \: hingga \: n $$
Step 5 - Untuk setiap unit Yi, lakukan langkah 6-9.
Step 6 - Hitung masukan bersih jaringan sebagai berikut -
$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limit_ {j} y_ {j} w_ {ji} $$
Step 7 - Terapkan aktivasi sebagai berikut di atas input bersih untuk menghitung output -
$$ y_ {i} \: = \ begin {kasus} 1 & jika \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {kasus} $$
Di sini $ \ theta_ {i} $ adalah ambang batas.
Step 8 - Siarkan keluaran ini yi ke semua unit lainnya.
Step 9 - Uji jaringan untuk hubungannya.
Evaluasi Fungsi Energi
Fungsi energi didefinisikan sebagai fungsi yang terikat dan fungsi yang tidak meningkat dari keadaan sistem.
Fungsi energi Ef, juga disebut Lyapunov function menentukan stabilitas jaringan Hopfield diskrit, dan dikarakterisasi sebagai berikut -
$$ E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ batas_ {i = 1} ^ n \ displaystyle \ sum \ batas_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limit_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limit_ {i = 1} ^ n \ theta_ {i} y_ {i} $$
Condition - Dalam jaringan yang stabil, setiap kali keadaan node berubah, fungsi energi di atas akan berkurang.
Misalkan saat node i telah mengubah status dari $ y_i ^ {(k)} $ menjadi $ y_i ^ {(k \: + \: 1)} $ lalu perubahan Energi $ \ Delta E_ {f} $ diberikan oleh relasi berikut
$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$
$$ = \: - \ kiri (\ begin {array} {c} \ displaystyle \ sum \ limit_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {larik} \ kanan) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$
$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$
Di sini $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $
Perubahan energi bergantung pada fakta bahwa hanya satu unit yang dapat memperbarui aktivasi pada satu waktu.
Jaringan Hopfield Berkelanjutan
Dibandingkan dengan jaringan Discrete Hopfield, jaringan kontinu memiliki waktu sebagai variabel kontinu. Ini juga digunakan dalam masalah asosiasi otomatis dan pengoptimalan seperti masalah penjual keliling.
Model - Model atau arsitektur dapat dibangun dengan menambahkan komponen listrik seperti amplifier yang dapat memetakan tegangan input ke tegangan output melalui fungsi aktivasi sigmoid.
Evaluasi Fungsi Energi
$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ limit_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$
Sini λ adalah parameter gain dan gri masukan konduktansi.