Pembelajaran dan Adaptasi
Seperti yang dikemukakan sebelumnya, JST sepenuhnya terinspirasi oleh cara kerja sistem saraf biologis, yakni otak manusia. Ciri yang paling mengesankan dari otak manusia adalah belajar, oleh karena itu ciri yang sama diperoleh oleh JST.
Apa Itu Belajar di ANN?
Pembelajaran pada dasarnya berarti melakukan dan menyesuaikan dengan perubahan itu sendiri ketika terjadi perubahan lingkungan. JST adalah suatu sistem yang kompleks atau lebih tepatnya dapat dikatakan sebagai sistem adaptif yang kompleks, yang dapat mengubah struktur internalnya berdasarkan informasi yang melewatinya.
Mengapa Itu Penting?
Menjadi sistem adaptif yang kompleks, pembelajaran di JST menyiratkan bahwa unit pemrosesan mampu mengubah perilaku input / outputnya karena perubahan lingkungan. Pentingnya pembelajaran di JST meningkat karena fungsi aktivasi tetap serta vektor input / output, ketika jaringan tertentu dibangun. Sekarang untuk mengubah perilaku input / output, kita perlu menyesuaikan bobotnya.
Klasifikasi
Ini dapat didefinisikan sebagai proses pembelajaran untuk membedakan data sampel ke dalam kelas yang berbeda dengan menemukan ciri-ciri umum antara sampel dari kelas yang sama. Misalnya, untuk melakukan pelatihan JST, kami memiliki beberapa sampel pelatihan dengan fitur unik, dan untuk melakukan pengujiannya kami memiliki beberapa sampel pengujian dengan fitur unik lainnya. Klasifikasi adalah contoh pembelajaran yang diawasi.
Aturan Pembelajaran Jaringan Neural
Kita tahu bahwa selama pembelajaran JST, untuk mengubah perilaku input / output, kita perlu menyesuaikan bobotnya. Oleh karena itu, diperlukan metode dengan bantuan bobot yang dapat dimodifikasi. Metode ini disebut Aturan belajar, yang merupakan algoritma atau persamaan. Berikut adalah beberapa aturan pembelajaran untuk jaringan saraf -
Aturan Belajar Hebbian
Aturan ini, salah satu yang tertua dan paling sederhana, diperkenalkan oleh Donald Hebb dalam bukunya The Organisation of Behavior pada tahun 1949. Ini adalah semacam pembelajaran umpan-maju, tanpa pengawasan.
Basic Concept - Aturan ini berdasarkan proposal yang diberikan oleh Hebb, yang menulis -
“Ketika akson sel A cukup dekat untuk merangsang sel B dan berulang kali atau terus-menerus mengambil bagian dalam menembakkannya, beberapa proses pertumbuhan atau perubahan metabolisme terjadi di satu atau kedua sel sehingga efisiensi A, sebagai salah satu sel yang menembakkan B , meningkat. "
Dari dalil di atas, kita dapat menyimpulkan bahwa hubungan antara dua neuron mungkin diperkuat jika neuron-neuron itu bekerja pada saat yang sama dan mungkin melemah jika mereka bekerja pada waktu yang berbeda.
Mathematical Formulation - Menurut aturan pembelajaran Hebbian, berikut adalah rumus untuk meningkatkan bobot koneksi di setiap langkah waktu.
$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$
Di sini, $ \ Delta w_ {ji} (t) $ = kenaikan dimana bobot koneksi meningkat pada langkah waktu t
$ \ alpha $ = kecepatan pembelajaran positif dan konstan
$ x_ {i} (t) $ = nilai input dari neuron pra-sinaptik pada langkah waktu t
$ y_ {i} (t) $ = keluaran neuron pra-sinaptik pada langkah waktu yang sama t
Aturan Pembelajaran Perceptron
Aturan ini adalah kesalahan yang mengoreksi algoritma pembelajaran yang diawasi dari jaringan feedforward lapisan tunggal dengan fungsi aktivasi linier, yang diperkenalkan oleh Rosenblatt.
Basic Concept- Sebagaimana sifatnya yang diawasi, untuk menghitung kesalahan akan dilakukan perbandingan antara keluaran yang diinginkan / target dengan keluaran yang sebenarnya. Jika ada perbedaan yang ditemukan, maka perubahan harus dilakukan pada bobot koneksi.
Mathematical Formulation - Untuk menjelaskan formulasi matematisnya, misalkan kita memiliki 'n' sejumlah vektor masukan hingga, x (n), bersama dengan vektor keluaran yang diinginkan / target t (n), di mana n = 1 ke N.
Sekarang keluaran 'y' dapat dihitung, seperti yang dijelaskan sebelumnya berdasarkan masukan bersih, dan fungsi aktivasi yang diterapkan di atas masukan bersih tersebut dapat dinyatakan sebagai berikut -
$$ y \: = \: f (y_ {in}) \: = \: \ begin {kasus} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {kasus} $$
Dimana θ adalah ambang batas.
Pembaruan bobot dapat dilakukan dalam dua kasus berikut -
Case I - kapan t ≠ y, kemudian
$$ w (baru) \: = \: w (lama) \: + \; tx $$
Case II - kapan t = y, kemudian
Tidak ada perubahan berat
Aturan Pembelajaran Delta (Aturan Widrow-Hoff)
Ini diperkenalkan oleh Bernard Widrow dan Marcian Hoff, juga disebut metode Least Mean Square (LMS), untuk meminimalkan kesalahan pada semua pola pelatihan. Ini adalah jenis algoritma pembelajaran yang diawasi dengan memiliki fungsi aktivasi berkelanjutan.
Basic Concept- Basis aturan ini adalah pendekatan penurunan-gradien, yang berlanjut selamanya. Aturan delta memperbarui bobot sinaptik untuk meminimalkan masukan bersih ke unit keluaran dan nilai target.
Mathematical Formulation - Untuk memperbarui bobot sinaptik, aturan delta diberikan oleh
$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$
Di sini $ \ Delta w_ {i} $ = perubahan berat untuk pola ke- i ;
$ \ alpha $ = kecepatan pembelajaran positif dan konstan;
$ x_ {i} $ = nilai masukan dari neuron pra-sinaptik;
$ e_ {j} $ = $ (t \: - \: y_ {in}) $, perbedaan antara keluaran yang diinginkan / target dan keluaran sebenarnya $ y_ {in} $
Aturan delta di atas hanya untuk satu unit keluaran.
Pembaruan bobot dapat dilakukan dalam dua kasus berikut -
Case-I - kapan t ≠ y, kemudian
$$ w (baru) \: = \: w (lama) \: + \: \ Delta w $$
Case-II - kapan t = y, kemudian
Tidak ada perubahan berat
Aturan Pembelajaran Kompetitif (Pemenang mengambil semua)
Ini berkaitan dengan pelatihan tanpa pengawasan di mana simpul keluaran mencoba bersaing satu sama lain untuk mewakili pola masukan. Untuk memahami aturan pembelajaran ini, kita harus memahami jaringan kompetitif yang diberikan sebagai berikut -
Basic Concept of Competitive Network- Jaringan ini seperti jaringan feedforward satu lapis dengan koneksi umpan balik antar keluaran. Hubungan antar output adalah tipe penghambat, ditunjukkan dengan garis putus-putus, yang berarti kompetitor tidak pernah mendukung dirinya sendiri.
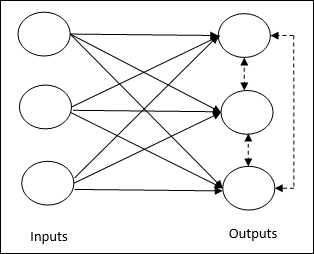
Basic Concept of Competitive Learning Rule- Seperti yang dikatakan sebelumnya, akan ada persaingan antar node keluaran. Oleh karena itu, konsep utamanya adalah selama pelatihan, unit keluaran dengan aktivasi tertinggi ke pola masukan tertentu, akan dinyatakan sebagai pemenang. Aturan ini juga disebut Pemenang-mengambil-semua karena hanya neuron pemenang yang diperbarui dan neuron lainnya dibiarkan tidak berubah.
Mathematical formulation - Berikut adalah tiga faktor penting untuk perumusan matematika dari aturan pembelajaran ini -
Condition to be a winner - Misalkan neuron $ y_ {k} $ ingin menjadi pemenang maka akan ada kondisi sebagai berikut -
$$ y_ {k} \: = \: \ begin {kasus} 1 & jika \: v_ {k} \:> \: v_ {j} \: untuk \: semua \: j, \: j \: \ neq \: k \\ 0 & sebaliknya \ end {kasus} $$
Ini berarti bahwa jika ada neuron, misalnya $ y_ {k} $ , ingin menang, maka bidang lokalnya yang diinduksi (keluaran unit penjumlahan), misalnya $ v_ {k} $, haruslah yang terbesar di antara semua neuron lainnya di jaringan.
Condition of sum total of weight - Batasan lain atas aturan pembelajaran kompetitif adalah, jumlah total bobot ke neuron keluaran tertentu akan menjadi 1. Misalnya, jika kita mempertimbangkan neuron k kemudian -
$$ \ displaystyle \ sum \ limit_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: untuk \: semua \: k $$
Change of weight for winner- Jika neuron tidak merespon pola masukan, maka tidak ada pembelajaran yang terjadi di neuron tersebut. Namun, jika neuron tertentu menang, maka bobot yang sesuai akan disesuaikan sebagai berikut
$$ \ Delta w_ {kj} \: = \: \ begin {kasus} - \ alpha (x_ {j} \: - \: w_ {kj}), & jika \: neuron \: k \: menang \\ 0, & jika \: neuron \: k \: kerugian \ end {kasus} $$
Di sini $ \ alpha $ adalah kecepatan pemelajaran.
Hal ini jelas menunjukkan bahwa kita mengunggulkan neuron pemenang dengan cara menyesuaikan bobotnya dan jika ada neuron yang hilang, maka kita tidak perlu bersusah payah menyesuaikan kembali bobotnya.
Aturan Pembelajaran Bintang Luar
Aturan ini, yang diperkenalkan oleh Grossberg, berkaitan dengan pembelajaran yang diawasi karena keluaran yang diinginkan diketahui. Ini juga disebut pembelajaran Grossberg.
Basic Concept- Aturan ini diterapkan pada neuron yang tersusun dalam sebuah lapisan. Ini dirancang khusus untuk menghasilkan keluaran yang diinginkand dari lapisan p neuron.
Mathematical Formulation - Penyesuaian bobot dalam aturan ini dihitung sebagai berikut
$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$
Sini d adalah keluaran neuron yang diinginkan dan $ \ alpha $ adalah kecepatan pemelajaran.