Optimasi Menggunakan Jaringan Hopfield
Optimasi adalah suatu tindakan untuk membuat sesuatu seperti desain, situasi, sumber daya, dan sistem menjadi seefektif mungkin. Menggunakan kemiripan antara fungsi biaya dan fungsi energi, kita dapat menggunakan neuron yang sangat saling berhubungan untuk memecahkan masalah pengoptimalan. Jaringan saraf semacam itu adalah jaringan Hopfield, yang terdiri dari satu lapisan yang berisi satu atau lebih neuron berulang yang terhubung sepenuhnya. Ini dapat digunakan untuk pengoptimalan.
Poin yang perlu diingat saat menggunakan jaringan Hopfield untuk pengoptimalan -
Fungsi energi harus minimal dari jaringan.
Ini akan menemukan solusi yang memuaskan daripada memilih salah satu dari pola yang disimpan.
Kualitas solusi yang ditemukan oleh jaringan Hopfield sangat bergantung pada status awal jaringan.
Masalah Penjual Bepergian
Menemukan rute terpendek yang ditempuh oleh salesman merupakan salah satu masalah komputasi yang dapat dioptimalkan dengan menggunakan jaringan syaraf tiruan Hopfield.
Konsep Dasar TSP
Travelling Salesman Problem (TSP) adalah masalah pengoptimalan klasik yang harus dilalui oleh seorang salesman nkota, yang terhubung satu sama lain, menjaga biaya serta jarak tempuh seminimal mungkin. Misalnya, penjual harus melakukan perjalanan ke 4 kota A, B, C, D dan tujuannya adalah menemukan tur melingkar terpendek, ABC – D, sehingga meminimalkan biaya, yang juga termasuk biaya perjalanan dari kota terakhir D ke kota pertama A.
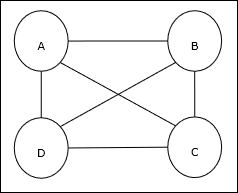
Representasi Matriks
Sebenarnya setiap wisata TSP n-kota bisa dinyatakan sebagai n × n matriks siapa ith baris menjelaskan ithlokasi kota. Matriks ini,M, untuk 4 kota A, B, C, D dapat dinyatakan sebagai berikut -
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Solusi oleh Jaringan Hopfield
Sambil mempertimbangkan solusi jaringan TSP by Hopfield ini, setiap node dalam jaringan sesuai dengan satu elemen dalam matriks.
Perhitungan Fungsi Energi
Untuk menjadi solusi yang optimal, fungsi energi harus minimum. Berdasarkan batasan berikut, kita dapat menghitung fungsi energi sebagai berikut -
Kendala-I
Batasan pertama, yang menjadi dasar kita akan menghitung fungsi energi, adalah bahwa satu elemen harus sama dengan 1 di setiap baris matriks M dan elemen lain di setiap baris harus sama dengan 0karena setiap kota hanya dapat menempati satu posisi dalam tur TSP. Batasan ini secara matematis dapat ditulis sebagai berikut -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: untuk \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Sekarang fungsi energi yang akan diminimalkan, berdasarkan batasan di atas, akan mengandung suku yang sebanding dengan -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n \ kiri (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j } \ end {larik} \ kanan) ^ 2 $$
Kendala-II
Seperti yang kita ketahui, di TSP satu kota dapat terjadi di posisi manapun dalam tur maka di setiap kolom matriks M, satu elemen harus sama dengan 1 dan elemen lainnya harus sama dengan 0. Batasan ini secara matematis dapat ditulis sebagai berikut -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: untuk \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Sekarang fungsi energi yang akan diminimalkan, berdasarkan batasan di atas, akan mengandung suku yang sebanding dengan -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n \ kiri (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j } \ end {larik} \ kanan) ^ 2 $$
Perhitungan Fungsi Biaya
Misalkan matriks persegi (n × n) dilambangkan dengan C menunjukkan matriks biaya TSP untuk n kota dimana n > 0. Berikut adalah beberapa parameter saat menghitung fungsi biaya -
Cx, y - Elemen matriks biaya menunjukkan biaya perjalanan dari kota x untuk y.
Kedekatan elemen A dan B dapat ditunjukkan oleh relasi berikut:
$$ M_ {x, i} \: = \: 1 \: \: dan \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Seperti yang kita ketahui, dalam Matriks nilai keluaran setiap node bisa 0 atau 1, maka untuk setiap pasangan kota A, B kita dapat menambahkan suku-suku berikut ke fungsi energi -
$$ \ displaystyle \ sum \ limit_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Berdasarkan fungsi biaya di atas dan nilai kendala, fungsi energi final E dapat diberikan sebagai berikut -
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {x} \ displaystyle \ sum \ limit_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limit_ {x} M_ {x, i} \ end {array} \ kanan) ^ 2 \ end {bmatrix} $$
Sini, γ1 dan γ2 adalah dua konstanta penimbangan.