Bokeh - Curve specializzate

Il bokeh.plotting L'API supporta i metodi per il rendering seguendo curve specializzate -

beizer ()

Questo metodo aggiunge una curva di Bézier all'oggetto figura. Una curva di Bézier è una curva parametrica utilizzata nella computer grafica. Altri usi includono la progettazione di caratteri e animazioni del computer, la progettazione dell'interfaccia utente e la traiettoria del cursore più liscia.

Nella grafica vettoriale, le curve di Bézier vengono utilizzate per modellare curve morbide che possono essere ridimensionate indefinitamente. Un "percorso" è una combinazione di curve di Bézier collegate.

Il metodo beizer () ha i seguenti parametri che sono definiti:

1	x0	Le coordinate x dei punti di partenza.
2	y0	Le coordinate y dei punti di partenza ..
3	x1	Le coordinate x dei punti finali.
4	y1	Le coordinate y dei punti finali.
5	cx0	Le coordinate x dei primi punti di controllo.
6	cy0	Le coordinate y dei primi punti di controllo.
7	cx1	Le coordinate x dei secondi punti di controllo.
8	cy1	Le coordinate y dei secondi punti di controllo.

Il valore predefinito per tutti i parametri è Nessuno.

Esempio

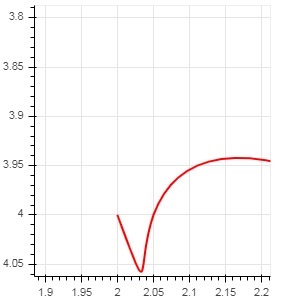
Il codice seguente genera una pagina HTML che mostra una curva di Bézier e una parabola nel grafico Bokeh -

x = 2
y = 4
xp02 = x+0.4
xp01 = x+0.1
xm01 = x-0.1
yp01 = y+0.2
ym01 = y-0.2
fig = figure(plot_width = 300, plot_height = 300)
fig.bezier(x0 = x, y0 = y, x1 = xp02, y1 = y, cx0 = xp01, cy0 = yp01,
cx1 = xm01, cy1 = ym01, line_color = "red", line_width = 2)

Produzione

quadratico ()

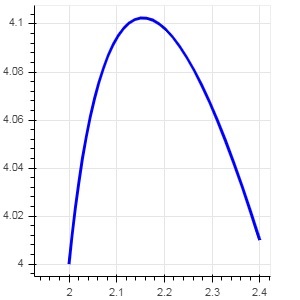
Questo metodo aggiunge un file parabola glyphalla figura del bokeh. La funzione ha gli stessi parametri di beizer (), trannecx0 e cx1.

Esempio

Il codice riportato di seguito genera una curva quadratica.

x = 2
y = 4
xp02 = x + 0.3
xp01 = x + 0.2
xm01 = x - 0.4
yp01 = y + 0.1
ym01 = y - 0.2
x = x,
y = y,
xp02 = x + 0.4,
xp01 = x + 0.1,
yp01 = y + 0.2,
fig.quadratic(x0 = x, y0 = y, x1 = x + 0.4, y1 = y + 0.01, cx = x + 0.1,
cy = y + 0.2, line_color = "blue", line_width = 3)

Produzione