Utilizzando una rete per trovare la superficie di un prisma triangolare

introduzione

In questa lezione, utilizziamo le reti di un prisma triangolare per trovare l'area della superficie del prisma triangolare.

Il net di una figura solida si forma quando una figura solida è dispiegata lungo i suoi bordi e le sue facce sono disposte in un modello in due dimensioni.

Le reti di prismi triangolari sono costituite da rettangoli e triangoli.

Using a net to find the surface area of a rectangular prism

Trovare le aree di ciascuno dei rettangoli e triangoli della rete di un prisma triangolare e sommare quelle aree fornisce l'area della superficie o l'area della superficie totale del prisma triangolare.

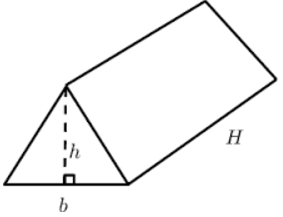
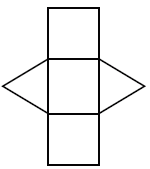
Ad esempio, lascia che le gambe di un triangolo rettangolo che è la base di un prisma triangolare siano 3 e 4 unità e l'altezza del prisma sia 10 unità. Dalla rete, possiamo vedere che ci sono due facce triangolari congruenti e tre facce rettangolari le cui aree sono le seguenti. 6 unità quadrate e (3 + 4 + 5) 10 = 120 unità quadrate. La superficie del prisma quindi = 2 (6) + 120 = 132 unità quadrate.

Surface Area of a Triangular Prism using Nets

Esempio 1:

Trova la superficie del seguente prisma triangolare usando net.