DAA-バイナリヒープ
ヒープにはいくつかの種類がありますが、この章では、バイナリヒープについて説明します。Abinary heapはデータ構造であり、完全な二分木に似ています。ヒープデータ構造は、以下で説明する順序付けプロパティに従います。通常、ヒープは配列で表されます。この章では、ヒープを次のように表します。H。
ヒープの要素は配列に格納されるため、開始インデックスを次のように考慮します。 1、の親ノードの位置 ith 要素はで見つけることができます ⌊ i/2 ⌋。の左子と右子ith ノードは位置にあります 2i そして 2i + 1。
バイナリヒープは、さらに次のいずれかに分類できます。 max-heap または min-heap 注文プロパティに基づきます。
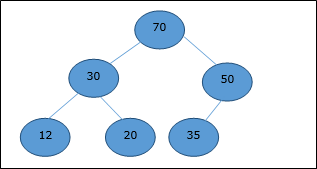
最大ヒープ
このヒープでは、ノードのキー値は最上位の子のキー値以上です。
したがって、 H[Parent(i)] ≥ H[i]
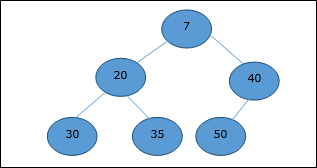
最小ヒープ
平均ヒープでは、ノードのキー値は最下位の子のキー値以下です。
したがって、 H[Parent(i)] ≤ H[i]
これに関連して、Max-Heapに関する基本的な操作を以下に示します。ヒープ内およびヒープからの要素の挿入および削除には、要素の再配置が必要です。したがって、Heapify 関数を呼び出す必要があります。
配列表現
完全な二分木は配列で表すことができ、レベル順トラバーサルを使用してその要素を格納します。
配列で表されるヒープ(以下に示す)について考えてみましょう。 H。
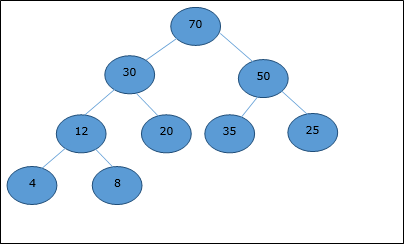
開始インデックスを次のように見なします 0、レベル順トラバーサルを使用して、要素は次のように配列に保持されます。
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ..。 |
| elements | 70 | 30 | 50 | 12 | 20 | 35 | 25 | 4 | 8 | ..。 |
このコンテキストでは、ヒープに対する操作はMax-Heapに関して表されています。
indexで要素の親のインデックスを見つけるには i、次のアルゴリズム Parent (numbers[], i) 使用されている。
Algorithm: Parent (numbers[], i)
if i == 1
return NULL
else
[i / 2]インデックスにある要素の左の子のインデックス i 次のアルゴリズムを使用して見つけることができます、 Left-Child (numbers[], i)。
Algorithm: Left-Child (numbers[], i)
If 2 * i ≤ heapsize
return [2 * i]
else
return NULLインデックスにある要素の右の子のインデックス i 次のアルゴリズムを使用して見つけることができます、 Right-Child(numbers[], i)。
Algorithm: Right-Child (numbers[], i)
if 2 * i < heapsize
return [2 * i + 1]
else
return NULL