DAA-頂点被覆
無向グラフの頂点被覆 G = (V, E) 頂点のサブセットです V' ⊆ V エッジの場合 (u, v) のエッジです G、次にどちらか u に V または v に V' または両方。
与えられた無向グラフで最大サイズの頂点被覆を見つけます。この最適な頂点被覆は、NP完全問題の最適化バージョンです。ただし、最適に近い頂点被覆を見つけることはそれほど難しくありません。
APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G]
while E' is not empty do
Let (u, v) be an arbitrary edge of E' c ← c U {u, v}
Remove from E' every edge incident on either u or v
return c例
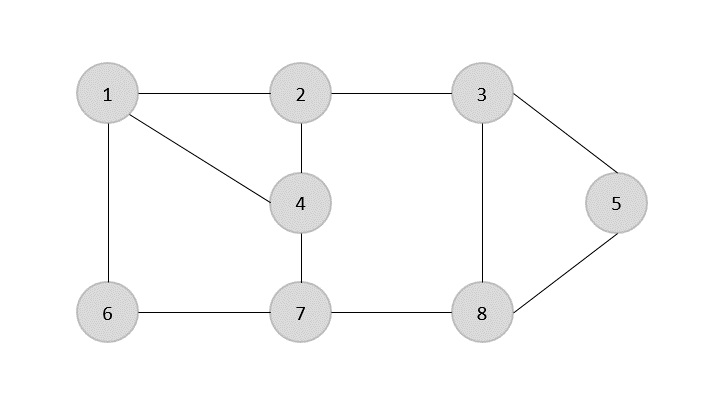
与えられたグラフのエッジのセットは-です
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
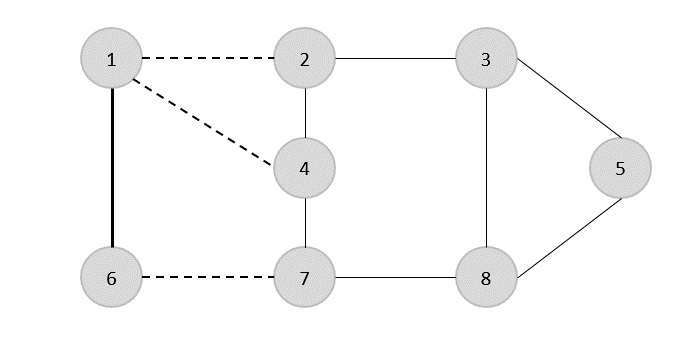
ここで、任意のエッジ(1,6)を選択することから始めます。頂点1または6に入射するすべてのエッジを削除し、カバーにエッジ(1,6)を追加します。
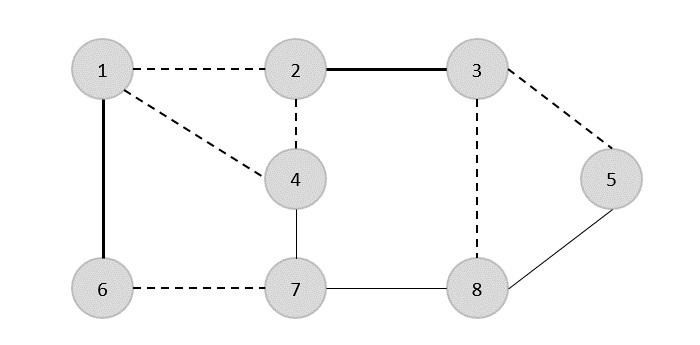
次のステップでは、別のエッジ(2,3)をランダムに選択しました
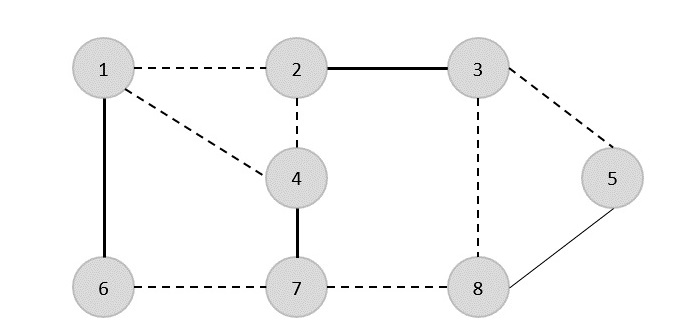
次に、別のエッジ(4,7)を選択します。
別のエッジ(8,5)を選択します。
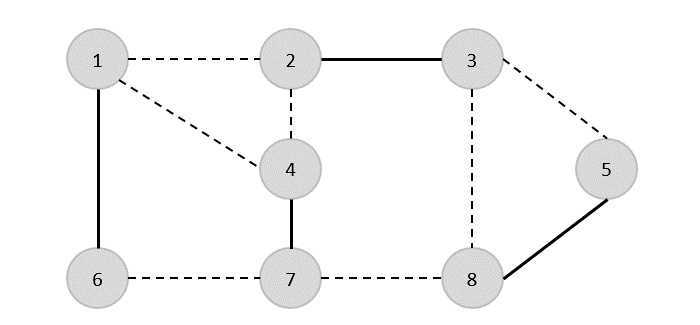
したがって、このグラフの頂点被覆は{1,2,4,5}です。
分析
このアルゴリズムの実行時間は次のとおりです。 O(V + E)、隣接リストを使用して表す E'。