DAA-多段グラフ

多段グラフ G = (V, E) 頂点がに分割されている有向グラフです k （どこ k > 1）互いに素なサブセットの数 S = {s₁,s₂,…,s_k}その結果、エッジ（U、V） Eであり、次いで、UЄS _I及びVЄS _{1 + 1}パーティション内のいくつかのサブセットおよび|s₁| = |s_k| = 1。

頂点 s Є s₁ と呼ばれます source と頂点 t Є s_k と呼ばれる sink。

G通常、加重グラフと見なされます。このグラフでは、エッジ（i、j）のコストはc（i、j）で表されます。したがって、ソースからのパスのコストs 沈む t このパスの各エッジのコストの合計です。

多段グラフの問題は、ソースから最小のコストでパスを見つけることです s 沈む t。

例

多段グラフの概念を理解するために、次の例を検討してください。

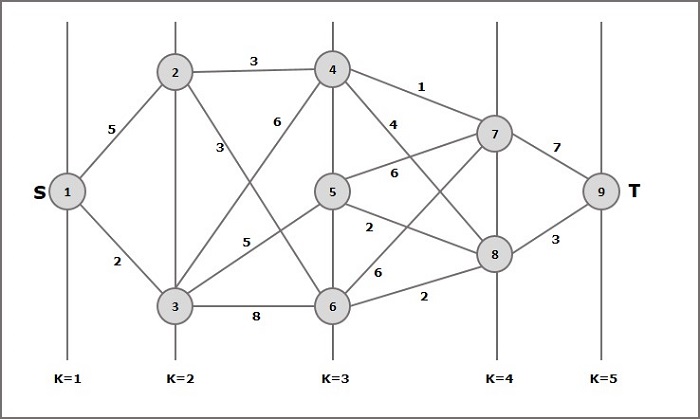
式に従って、コストを計算する必要があります (i, j) 次の手順を使用します

ステップ-1：コスト（K-2、j）

このステップでは、3つのノード（ノード4、5、6）が次のように選択されます。 j。したがって、このステップで最小コストを選択するための3つのオプションがあります。

Cost（3、4）= min {c（4、7）+ Cost（7、9）、c（4、8）+ Cost（8、9）} = 7

Cost（3、5）= min {c（5、7）+ Cost（7、9）、c（5、8）+ Cost（8、9）} = 5

Cost（3、6）= min {c（6、7）+ Cost（7、9）、c（6、8）+ Cost（8、9）} = 5

ステップ2：コスト（K-3、j）

ステージk-3 = 2には2と3の2つのノードがあるため、2つのノードがjとして選択されます。したがって、値i = 2とj = 2と3です。

Cost（2、2）= min {c（2、4）+ Cost（4、8）+ Cost（8、9）、c（2、6）+

Cost（6、8）+ Cost（8、9）} = 8

Cost（2、3）= {c（3、4）+ Cost（4、8）+ Cost（8、9）、c（3、5）+ Cost（5、8）+ Cost（8、9）、 c（3、6）+コスト（6、8）+コスト（8、9）} = 10

ステップ-3：コスト（K-4、j）

コスト（1、1）= {c（1、2）+コスト（2、6）+コスト（6、8）+コスト（8、9）、c（1、3）+コスト（3、5）+ Cost（5、8）+ Cost（8、9））} = 12

c（1、3）+ Cost（3、6）+ Cost（6、8 + Cost（8、9））} = 13

したがって、最小コストのパスは次のようになります。 1→ 3→ 5→ 8→ 9。