DAA-最適なコストの二分木

二分探索木（BST）は、キー値が内部ノードに格納されているツリーです。外部ノードはヌルノードです。キーは辞書式順序で並べられます。つまり、内部ノードごとに、左側のサブツリーのすべてのキーがノードのキーよりも小さく、右側のサブツリーのすべてのキーが大きくなります。

各キーを検索する頻度がわかっている場合、ツリー内の各ノードにアクセスするための予想コストを計算するのは非常に簡単です。最適な二分探索木はBSTであり、各ノードを見つけるための予想コストは最小限です。

BST内の要素の検索時間は O(n)、一方、平衡二分探索木では、検索時間は O(log n)。この場合も、Optimal Cost Binary Search Treeで検索時間を改善し、最も頻繁に使用されるデータをルートおよびルート要素の近くに配置し、最も使用頻度の低いデータを葉の近くおよび葉に配置します。

ここでは、最適な二分探索木アルゴリズムが提示されます。まず、提供されたセットからBSTを構築しますn 個別のキーの数 < k₁, k₂, k₃, ... k_n >。ここでは、キーにアクセスする確率を想定していますK_i です p_i。いくつかのダミーキー（d₀, d₁, d₂, ... d_n）キーセットに存在しない値に対して一部の検索が実行される可能性があるため、追加されます K。ダミーキーごとに、d_i アクセスの確率は q_i。

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := qi - 1 
   w[i, i - 1] := qi - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + pj + qj 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root

分析

アルゴリズムには O (n³) 時間、3つがネストされているので forループが使用されます。これらのループのそれぞれはせいぜい引き受けますn 値。

例

次のツリーを考慮すると、コストは2.80ですが、これは最適な結果ではありません。

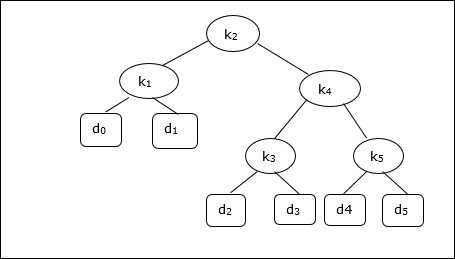
ノード	深さ	確率	貢献
k 1	1	0.15	0.30
k 2	0	0.10	0.10
k 3	2	0.05	0.15
k 4	1	0.10	0.20
k 5	2	0.20	0.60
d 0	2	0.05	0.15
d 1	2	0.10	0.30
d 2	3	0.05	0.20
d 3	3	0.05	0.20
d 4	3	0.05	0.20
d 5	3	0.10	0.40
Total			2.80

この章で説明するアルゴリズムを使用して最適なソリューションを取得するために、次の表が生成されます。

次の表では、列インデックスは i 行インデックスは j。

e	1	2	3	4	5	6
5	2.75	2.00	1.30	0.90	0.50	0.10
4	1.75	1.20	0.60	0.30	0.05
3	1.25	0.70	0.25	0.05
2	0.90	0.40	0.05
1	0.45	0.10
0	0.05

w	1	2	3	4	5	6
5	1.00	0.80	0.60	0.50	0.35	0.10
4	0.70	0.50	0.30	0.20	0.05
3	0.55	0.35	0.15	0.05
2	0.45	0.25	0.05
1	0.30	0.10
0	0.05

ルート	1	2	3	4	5
5	2	4	5	5	5
4	2	2	4	4
3	2	2	3
2	1	2
1	1

これらのテーブルから、最適なツリーを形成できます。