DAA-最短経路

ダイクストラのアルゴリズム

ダイクストラのアルゴリズムは、有向加重グラフG =（V、E）で単一ソースの最短経路問題を解きます。ここで、すべてのエッジは非負です（つまり、各エッジ（u、v ）に対してw（u、v） ≥0 ）ЄE）。

次のアルゴリズムでは、1つの関数を使用します Extract-Min()、最小のキーを持つノードを抽出します。

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

分析

このアルゴリズムの複雑さは、Extract-Min関数の実装に完全に依存しています。最小抽出関数が線形検索を使用して実装されている場合、このアルゴリズムの複雑さは次のようになります。O(V² + E)。

このアルゴリズムでは、min-heapを使用すると Extract-Min() 関数はからノードを返すように動作します Q 最小のキーを使用すると、このアルゴリズムの複雑さをさらに軽減できます。

例

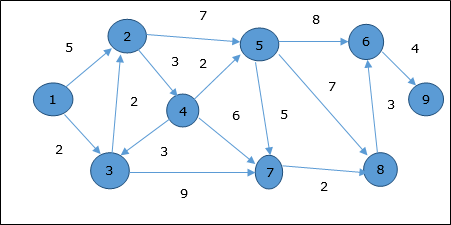
頂点について考えてみましょう 1 そして 9それぞれ開始頂点と宛先頂点として。最初に、開始頂点を除くすべての頂点は∞でマークされ、開始頂点はでマークされます。0。

バーテックス	初期	ステップ1V 1	ステップ2V 3	ステップ3V 2	ステップ4V 4	ステップ5V 5	ステップ6V 7	ステップ7V 8	ステップ8V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

したがって、頂点の最小距離 9 頂点から 1 です 20。そして、その道は

1→3→7→8→6→9

このパスは、先行情報に基づいて決定されます。

ベルマンフォードアルゴリズム

このアルゴリズムは、有向グラフの単一ソース最短経路問題を解決します G = (V, E)エッジの重みが負になる場合があります。さらに、負の重み付きサイクルが存在しない場合は、このアルゴリズムを適用して最短経路を見つけることができます。

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

分析

最初 for ループは初期化に使用され、 O(V)回。次for ループ実行|V - 1| エッジを通過します。O(E) 回。

したがって、ベルマンフォードアルゴリズムはで実行されます O(V, E) 時間。

例

次の例は、ベルマンフォードアルゴリズムがどのように機能するかを段階的に示しています。このグラフには負のエッジがありますが、負のサイクルはありません。したがって、この手法を使用して問題を解決できます。

初期化時に、ソースを除くすべての頂点は∞でマークされ、ソースはでマークされます。 0。

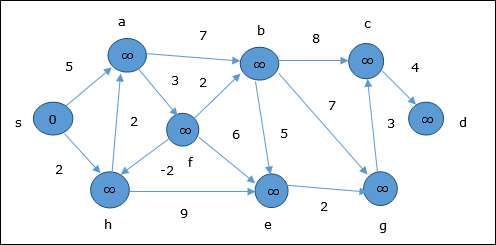
最初のステップでは、ソースから到達可能なすべての頂点が最小コストで更新されます。したがって、頂点a そして h 更新されます。

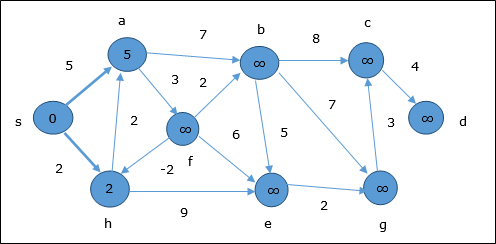
次のステップでは、頂点 a, b, f そして e 更新されます。

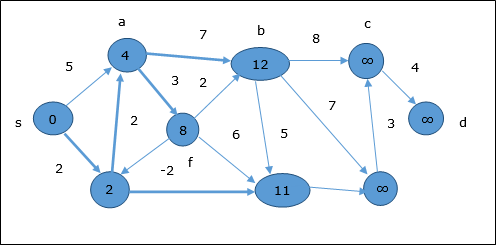
同じロジックに従って、このステップでは頂点 b, f, c そして g 更新されます。

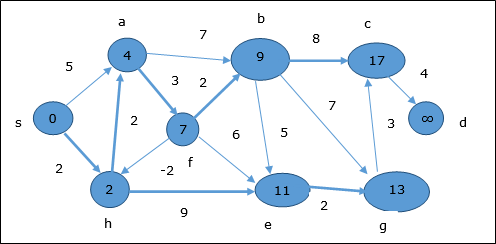
ここでは、頂点 c そして d 更新されます。

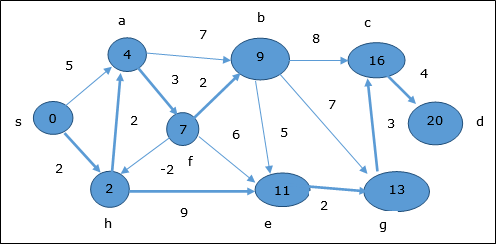
したがって、頂点間の最小距離 s および頂点 d です 20。

先行情報に基づくと、パスはs→h→e→g→c→dです。