DAA-最適なマージパターン
異なる長さのソートされたファイルのセットを単一のソートされたファイルにマージします。結果のファイルが最小時間で生成される最適なソリューションを見つける必要があります。
ソートされたファイルの数が指定されている場合、それらを1つのソートされたファイルにマージする方法はたくさんあります。このマージはペアごとに実行できます。したがって、このタイプのマージは次のように呼ばれます。2-way merge patterns。
ペアリングが異なれば必要な時間も異なるため、この戦略では、多くのファイルをマージする最適な方法を決定する必要があります。各ステップで、2つの最短シーケンスがマージされます。
マージするには p-record file と q-record file おそらく必要です p + q レコードの移動は、当然の選択ですが、各ステップで2つの最小のファイルをマージします。
双方向のマージパターンは、バイナリマージツリーで表すことができます。のセットを考えてみましょうn ソートされたファイル {f1, f2, f3, …, fn}。最初は、この各要素は単一ノードの二分木と見なされます。この最適解を見つけるために、次のアルゴリズムが使用されます。
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);このアルゴリズムの最後では、ルートノードの重みが最適なコストを表します。
例
私たちは、F、所定のファイルを考える1 F、2、fが3で、f 4及びf 5のそれぞれの要素の20、30、10、5及び30の数です。
提供された順序に従ってマージ操作が実行される場合、
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
したがって、操作の総数は次のようになります。
50 + 60 + 65 + 95 = 270
さて、疑問が生じます。より良い解決策はありますか?
サイズに従って番号を昇順で並べ替えると、次のシーケンスが得られます。
f4, f3, f1, f2, f5
したがって、マージ操作はこのシーケンスで実行できます
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
したがって、操作の総数は次のようになります。
15 + 35 + 65 + 95 = 210
明らかに、これは前のものよりも優れています。
これに関連して、このアルゴリズムを使用して問題を解決します。
初期セット

ステップ1
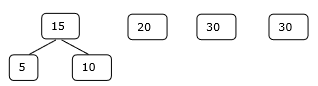
ステップ2
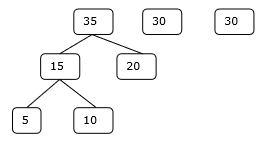
ステップ-3
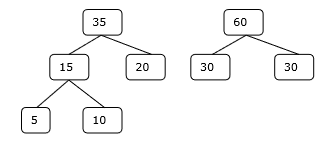
ステップ-4
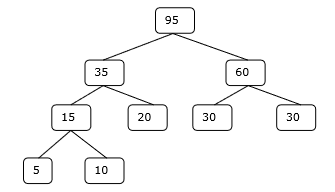
したがって、このソリューションでは15 + 35 + 60 + 95 = 205回の比較が行われます。