デジタル通信-デルタ変調

より良いサンプリングを実現するには、信号のサンプリングレートをナイキストレートよりも高くする必要があります。差分PCMでのこのサンプリング間隔が大幅に短縮された場合、サンプル間の振幅の差は、差が1-bit quantizationの場合、ステップサイズは非常に小さくなります。 Δ （デルタ）。

デルタ変調

サンプリングレートがはるかに高く、量子化後のステップサイズの値が小さい変調のタイプ Δ、そのような変調は次のように呼ばれます delta modulation。

デルタ変調の機能

以下は、デルタ変調の機能の一部です。

信号相関を最大限に活用するために、オーバーサンプリングされた入力が取得されます。
量子化の設計は単純です。
入力シーケンスは、ナイキストレートよりもはるかに高くなっています。
品質は中程度です。
変調器と復調器の設計は単純です。
出力波形の階段近似。
ステップサイズは非常に小さいです。 Δ （デルタ）。
ビットレートはユーザーが決定できます。
これには、より簡単な実装が含まれます。

デルタ変調は、DPCM技術の簡略化された形式であり、次のようにも表示されます。 1-bit DPCM scheme。サンプリング間隔が短くなると、信号の相関が高くなります。

デルタ変調器

Delta Modulatorは、1ビットの量子化器と遅延回路、および2つのサマー回路で構成されています。以下は、デルタ変調器のブロック図です。

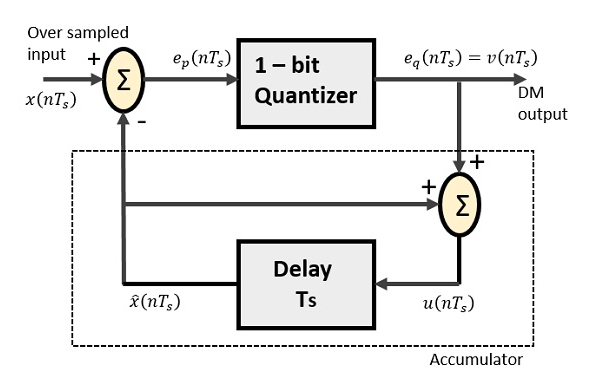
DPCMの予測回路は、DMの単純な遅延回路に置き換えられています。

上の図から、次のような表記があります。

$ x（nT_ {s}）$ =オーバーサンプリングされた入力
$ e_ {p}（nT_ {s}）$ =夏の出力と量子化器の入力
$ e_ {q}（nT_ {s}）$ =量子化器の出力= $ v（nT_s）$
$ \ widehat {x}（nT_ {s}）$ =遅延回路の出力
$ u（nT_ {s}）$ =遅延回路の入力

これらの表記法を使用して、デルタ変調のプロセスを理解しようとします。

$ e_ {p}（nT_ {s}）= x（nT_ {s}）-\ widehat {x}（nT_ {s}）$

---------式1

$ = x（nT_ {s}）-u（[n-1] T_ {s}）$

$ = x（nT_ {s}）-[\ widehat {x} [[n-1] T_ {s}] + v [[n-1] T_ {s}]] $

---------式2

さらに、

$ v（nT_ {s}）= e_ {q}（nT_ {s}）= S.sig。[e_ {p}（nT_ {s}）] $

---------式3

$ u（nT_ {s}）= \ widehat {x}（nT_ {s}）+ e_ {q}（nT_ {s}）$

どこ、

$ \ widehat {x}（nT_ {s}）$ =遅延回路の以前の値
$ e_ {q}（nT_ {s}）$ =量子化器の出力= $ v（nT_s）$

したがって、

$ u（nT_ {s}）= u（[n-1] T_ {s}）+ v（nT_ {s}）$

---------式4

つまり、

The present input of the delay unit

= (The previous output of the delay unit) + (the present quantizer output)

蓄積の条件がゼロであると仮定すると、

$ u（nT_ {s}）= S \ displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_ {p}（jT_ {s}）] $

Accumulated version of DM output = $ \ displaystyle \ sum \ limits_ {j = 1} ^ nv（jT_ {s}）$

---------式5

さて、注意してください

$ \ widehat {x}（nT_ {s}）= u（[n-1] T_ {s}）$

$ = \ displaystyle \ sum \ limits_ {j = 1} ^ {n-1} v（jT_ {s}）$

---------式6

ディレイユニットの出力は、1サンプル遅れたアキュムレータ出力です。

式5と6から、復調器の可能な構造が得られます。

階段近似波形は、デルタとしてのステップサイズを持つデルタ変調器の出力になります（Δ）。波形の出力品質は中程度です。

デルタ復調器

デルタ復調器は、ローパスフィルタ、サマー、および遅延回路で構成されています。ここでは予測回路が削除されているため、復調器に想定される入力は与えられません。

以下は、デルタ復調器の図です。

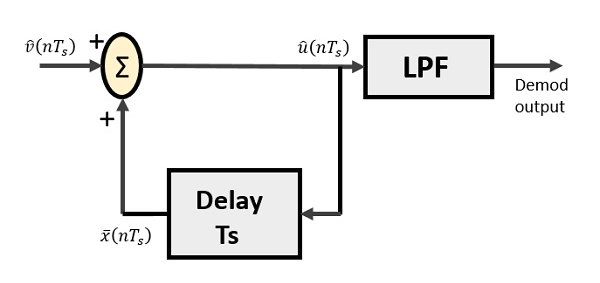
上の図から、次のような表記があります。

$ \ widehat {v}（nT_ {s}）$は入力サンプルです
$ \ widehat {u}（nT_ {s}）$は夏の出力です
$ \ bar {x}（nT_ {s}）$は遅延出力です

バイナリシーケンスは、復調器への入力として与えられます。階段近似出力はLPFに与えられます。

ローパスフィルターは多くの理由で使用されますが、主な理由は帯域外信号のノイズ除去です。送信機で発生する可能性のあるステップサイズエラーは、granular noise、ここでは削除されます。ノイズが存在しない場合、変調器の出力は復調器の入力と等しくなります。

DPCMに対するDMの利点

1ビット量子化器
変調器と復調器の非常に簡単な設計

ただし、DMにはノイズがあります。

勾配過負荷歪み（ Δ 小さいです）
粒状ノイズ（ Δ は大きい）

アダプティブデルタ変調（ADM）

デジタル変調では、出力波の品質に影響を与えるステップサイズを決定するという特定の問題に遭遇しました。

変調信号の急勾配では大きなステップサイズが必要であり、メッセージの勾配が小さい場合は小さなステップサイズが必要です。その過程で細部が見落とされます。したがって、希望する方法でサンプリングを取得するために、要件に応じてステップサイズの調整を制御できるとよいでしょう。これがのコンセプトですAdaptive Delta Modulation。

以下は、アダプティブデルタ変調器のブロック図です。

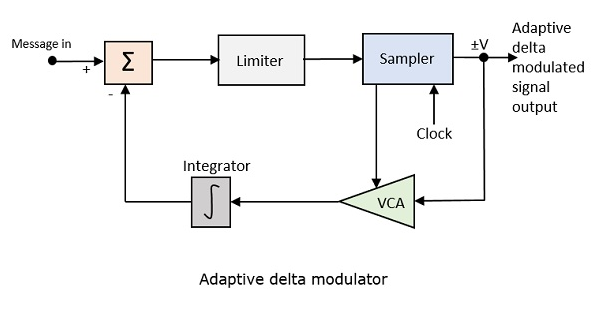
電圧制御アンプのゲインは、サンプラーからの出力信号によって調整されます。アンプのゲインがステップサイズを決定し、両方が比例します。

ADMは、現在のサンプルの値と次のサンプルの予測値の差を定量化します。可変ステップ高さを使用して次の値を予測し、急速に変化する値を忠実に再現します。