ソースコーディング定理
ディスクリートメモリレスソースによって生成されたコードは、効率的に表現する必要があります。これは、通信における重要な問題です。これを実現するために、これらのソースコードを表すコードワードがあります。
たとえば、電信では、アルファベットがで示されるモールス信号を使用します Marks そして Spaces。手紙の場合E 主に使用されると見なされ、それはによって示されます “.” 手紙が Q めったに使用されない、で示されます “--.-”
ブロック図を見てみましょう。
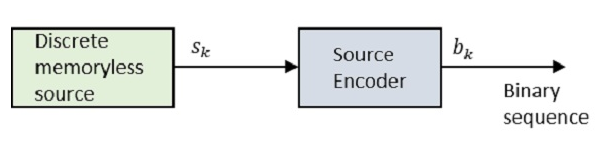
どこ Sk ディスクリートメモリレスソースの出力であり、 bk は、で表されるソースエンコーダの出力です。 0s そして 1s。
エンコードされたシーケンスは、受信機で便利にデコードされるようなものです。
ソースにアルファベットが含まれていると仮定しましょう k 異なるシンボルとその kth シンボル Sk 確率で発生します Pk、 どこ k = 0, 1…k-1。
バイナリコードワードをシンボルに割り当てましょう Sk、長さのあるエンコーダによる lk、ビット単位で測定。
したがって、ソースエンコーダの平均コードワード長Lを次のように定義します。
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L ソースシンボルあたりの平均ビット数を表します
$ L_ {min} = \:最小\:可能\:値\:の\:\ overline {L} $の場合
次に coding efficiency 次のように定義できます
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
$ \ overline {L} \ geq L_ {min} $を使用すると、$ \ eta \ leq 1 $になります。
ただし、$ \ eta = 1 $の場合、ソースエンコーダは効率的であると見なされます。
このためには、値$ L_ {min} $を決定する必要があります。
定義を参照してみましょう。「離散的なメモリレスのエントロピーソース$ H(\ delta)$が与えられた場合、平均コードワード長L すべてのソースエンコーディングは、$ \ overline {L} \ geq H(\ delta)$として制限されます。」
簡単に言うと、コードワード(例:QUEUEという単語のモールス信号は-.- ..- ..-。)は、常にソースコード(例ではQUEUE)以上です。つまり、コードワードの記号は、ソースコードのアルファベット以上です。
したがって、$ L_ {min} = H(\ delta)$の場合、エントロピー$ H(\ delta)$に関するソースエンコーダの効率は次のように記述できます。
$$ \ eta = \ frac {H(\ delta)} {\ overline {L}} $$
このソースコーディング定理は、 noiseless coding theoremエラーのないエンコーディングを確立するためです。とも呼ばれますShannon’s first theorem。