2D 변환
변환은 규칙을 적용하여 일부 그래픽을 다른 것으로 변경하는 것을 의미합니다. 변환, 확대 또는 축소, 회전, 기울이기 등과 같은 다양한 유형의 변환이있을 수 있습니다. 변환이 2D 평면에서 발생하는 것을 2D 변환이라고합니다.
변환은 컴퓨터 그래픽에서 화면의 그래픽 위치를 변경하고 크기 나 방향을 변경하는 데 중요한 역할을합니다.
동종 좌표
변환, 회전 및 크기 조정과 같은 일련의 변환을 수행하려면 순차적 프로세스를 따라야합니다.
- 좌표를 번역하고,
- 변환 된 좌표를 회전 한 다음
- 회전 된 좌표의 크기를 조정하여 합성 변환을 완료합니다.
이 과정을 단축하려면 2x2 변환 행렬 대신 3x3 변환 행렬을 사용해야합니다. 2x2 행렬을 3x3 행렬로 변환하려면 추가 더미 좌표 W를 추가해야합니다.
이런 식으로 우리는 2 개의 숫자 대신 3 개의 숫자로 점을 나타낼 수 있습니다. Homogenous Coordinate체계. 이 시스템에서 우리는 행렬 곱셈에서 모든 변환 방정식을 나타낼 수 있습니다. 모든 데카르트 점 P (X, Y)는 P '(X h , Y h , h)에 의해 동종 좌표로 변환 될 수 있습니다 .
번역
번역은 개체를 화면의 다른 위치로 이동합니다. 변환 좌표 (t x , t y )를 원래 좌표 (X, Y)에 추가하여 새 좌표 (X ', Y') 를 가져옴으로써 2D에서 점을 변환 할 수 있습니다 .
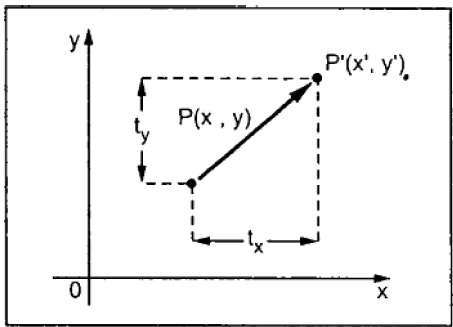
위의 그림에서 다음과 같이 쓸 수 있습니다.
X’ = X + tx
Y’ = Y + ty
쌍 (t x , t y )을 변환 벡터 또는 시프트 벡터라고합니다. 위의 방정식은 열 벡터를 사용하여 나타낼 수도 있습니다.
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
우리는 그것을 다음과 같이 쓸 수 있습니다.
P’ = P + T
회전
회전에서 우리는 원점으로부터 특정 각도 θ (세타)로 물체를 회전시킵니다. 다음 그림에서 점 P (X, Y)가 원점에서 거리 r과 함께 수평 X 좌표에서 각도 φ에 위치 함을 알 수 있습니다.
각도 θ로 회전한다고 가정 해 봅시다. 새 위치로 회전하면 새 점 P '(X', Y ')가 생성됩니다.

표준 삼각법을 사용하여 점 P (X, Y)의 원래 좌표는 다음과 같이 나타낼 수 있습니다.
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
같은 방식으로 점 P '(X', Y ')를 다음과 같이 표현할 수 있습니다.
$ {x} '= r \ : cos \ : \ left (\ phi \ : + \ : \ theta \ right) = r \ : cos \ : \ phi \ : cos \ : \ theta \ : − \ : r \ : sin \ : \ phi \ : sin \ : \ theta ....... (3) $
$ {y} '= r \ : sin \ : \ left (\ phi \ : + \ : \ theta \ right) = r \ : cos \ : \ phi \ : sin \ : \ theta \ : + \ : r \ : sin \ : \ phi \ : cos \ : \ theta ....... (4) $
(3)과 (4)에서 방정식 (1)과 (2)를 각각 대입하면
$ {x} '= x \ : cos \ : \ theta − \ : y \ : sin \ : \ theta $
$ {y} '= x \ : sin \ : \ theta + \ : y \ : cos \ : \ theta $
위의 방정식을 행렬 형태로 표현하면,
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} OR $$
P '= P. 아르 자형
여기서 R은 회전 행렬입니다.
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
회전 각도는 양수 및 음수 일 수 있습니다.
양의 회전 각도의 경우 위의 회전 행렬을 사용할 수 있습니다. 그러나 음의 각도 회전의 경우 매트릭스는 아래와 같이 변경됩니다.
$$ R = \ begin {bmatrix} cos (− \ theta) & sin (− \ theta) \\ -sin (− \ theta) & cos (− \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ because cos (− \ theta) = cos \ theta \; and \; sin (− \ theta) = −sin \ theta \ right) $$
스케일링
개체의 크기를 변경하려면 크기 조정 변환이 사용됩니다. 크기 조정 프로세스에서 개체의 크기를 확장하거나 압축합니다. 원하는 결과를 얻기 위해 개체의 원래 좌표에 배율 인수를 곱하여 배율을 조정할 수 있습니다.
원래 좌표가 (X, Y)이고 배율 인수가 (S X , S Y )이고 생성 된 좌표가 (X ', Y') 라고 가정 해 보겠습니다 . 이것은 아래와 같이 수학적으로 표현 될 수 있습니다.
X' = X . SX and Y' = Y . SY
배율 계수 S X , S Y 는 각각 X 및 Y 방향으로 개체의 배율을 조정합니다. 위의 방정식은 다음과 같이 행렬 형태로도 표현할 수 있습니다.
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
또는
P’ = P . S
여기서 S는 스케일링 행렬입니다. 확장 프로세스는 다음 그림에 나와 있습니다.
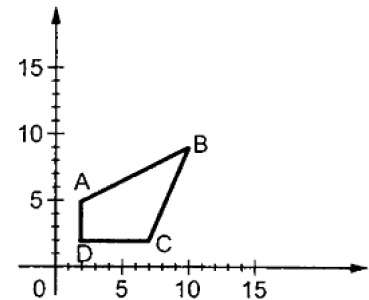
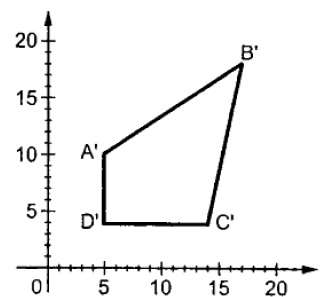
스케일링 계수 S에 1보다 작은 값을 제공하면 객체의 크기를 줄일 수 있습니다. 1보다 큰 값을 제공하면 개체의 크기를 늘릴 수 있습니다.
반사
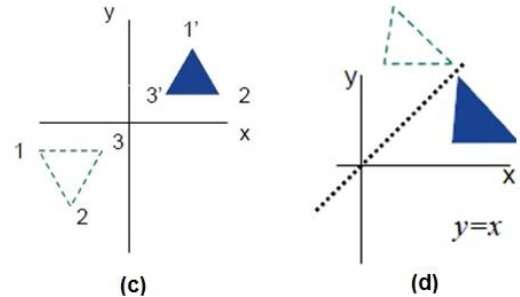
반사는 원래 물체의 거울 이미지입니다. 즉, 180 ° 회전 동작이라고 할 수 있습니다. 반사 변환에서 개체의 크기는 변경되지 않습니다.
다음 그림은 각각 X 및 Y 축과 원점에 대한 반사를 보여줍니다.
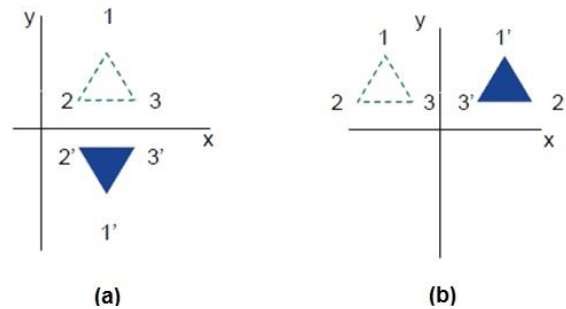
전단
물체의 모양을 기울이는 변형을 전단 변형이라고합니다. 두 가지 전단 변환이 있습니다.X-Shear 과 Y-Shear. 하나는 X 좌표 값을 이동하고 다른 하나는 Y 좌표 값을 이동합니다. 하나; 두 경우 모두 하나의 좌표 만 해당 좌표를 변경하고 다른 좌표는 해당 값을 유지합니다. 전단은 또한 다음과 같이 불립니다.Skewing.
X-Shear
X-Shear는 Y 좌표를 유지하고 X 좌표가 변경되어 아래 그림과 같이 수직선이 오른쪽 또는 왼쪽으로 기울어집니다.
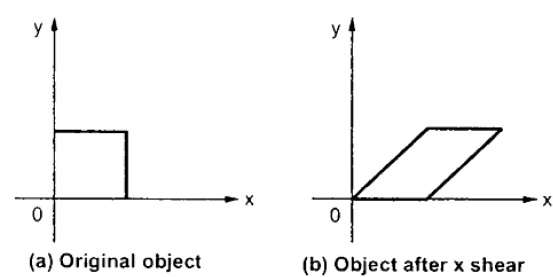
X-Shear에 대한 변환 행렬은 다음과 같이 나타낼 수 있습니다.
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . 엑스
X '= X
Y 전단
Y-Shear는 X 좌표를 유지하고 Y 좌표를 변경하여 다음 그림과 같이 수평선이 위아래로 기울어지는 선으로 변환되도록합니다.
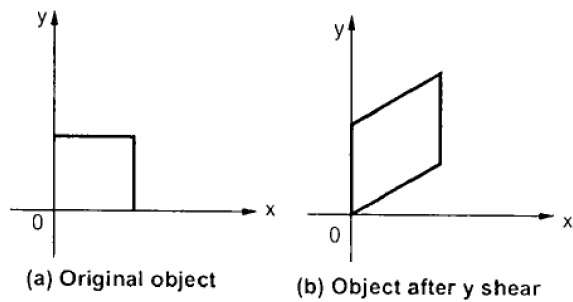
Y-Shear는 다음과 같이 행렬로 표현 될 수 있습니다.
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X '= X + Sh x . 와이
Y '= Y
복합 변환
평면 T1의 변환 후 제 2 평면 변환 T2가 뒤 따르면 결과 자체는 그 순서대로 취해진 T1 및 T2의 구성 인 단일 변환 T로 표현 될 수 있습니다. T = T1 ∙ T2로 표기됩니다.
복합 변환은 변환 행렬을 연결하여 결합 된 변환 행렬을 얻을 수 있습니다.
결합 된 행렬-
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
여기서 [Ti]는 다음의 조합입니다.
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
일반적으로 행렬 곱셈이 누적되지 않기 때문에 변환 순서의 변경은 다른 결과를 가져옵니다. 즉 [A]입니다. [B] ≠ [B]. [A]와 곱셈의 순서. 변환을 구성하는 기본 목적은 일련의 변환을 차례로 적용하는 대신 하나의 구성된 변환을 포인트에 적용하여 효율성을 얻는 것입니다.
예를 들어, 임의의 점 (X p , Y p ) 을 중심으로 객체를 회전하려면 세 단계를 수행해야합니다.
- 점 (X p , Y p )을 원점으로 변환합니다.
- 원점을 기준으로 회전합니다.
- 마지막으로 회전 중심을 원래 위치로 되돌립니다.