컴퓨터 그래픽-퀵 가이드
컴퓨터 그래픽은 프로그래밍의 도움을 받아 컴퓨터 화면에 그림을 그리는 예술입니다. 여기에는 데이터의 계산, 생성 및 조작이 포함됩니다. 즉, 컴퓨터 그래픽은 이미지의 생성과 조작을위한 렌더링 도구라고 말할 수 있습니다.
음극선 관
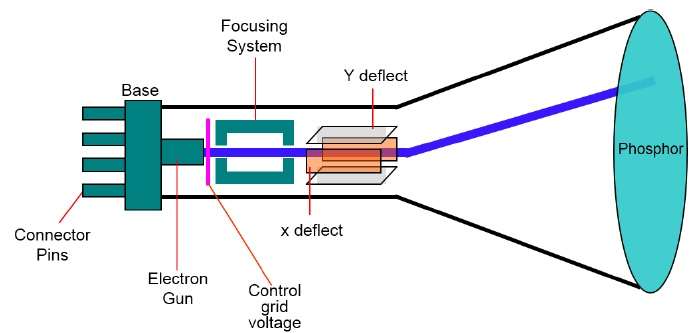
그래픽 시스템의 기본 출력 장치는 비디오 모니터입니다. 비디오 모니터의 주요 요소는Cathode Ray Tube (CRT), 다음 그림에 나와 있습니다.
CRT의 작동은 매우 간단합니다.
전자총은 전자빔 (음극선)을 방출합니다.
전자빔은 인광체 코팅 스크린의 지정된 위치로 향하는 초점 및 편향 시스템을 통과합니다.
빔이 스크린에 닿으면 형광체는 전자 빔이 접촉하는 각 위치에서 작은 빛을 방출합니다.
전자빔을 동일한 화면 지점 위로 빠르게 다시 향하게하여 그림을 다시 그립니다.
화면에 개체를 표시 할 수있는 두 가지 방법 (랜덤 스캔 및 래스터 스캔)이 있습니다.
래스터 스캔
래스터 스캔 시스템에서 전자 빔은 화면을 가로 질러 위에서 아래로 한 번에 한 행씩 스윕됩니다. 전자 빔이 각 행을 가로 질러 이동함에 따라 빔 강도가 켜지고 꺼져 조명 된 점의 패턴을 만듭니다.
사진 정의는라는 메모리 영역에 저장됩니다. Refresh Buffer 또는 Frame Buffer. 이 메모리 영역은 모든 화면 포인트에 대한 강도 값 세트를 보유합니다. 저장된 강도 값은 새로 고침 버퍼에서 검색되고 다음 그림과 같이 한 번에 한 행 (스캔 라인) 화면에 "도색"됩니다.
각 화면 지점은 pixel (picture element) 또는 pel. 각 스캔 라인의 끝에서 전자 빔은 화면의 왼쪽으로 돌아가 다음 스캔 라인을 표시하기 시작합니다.
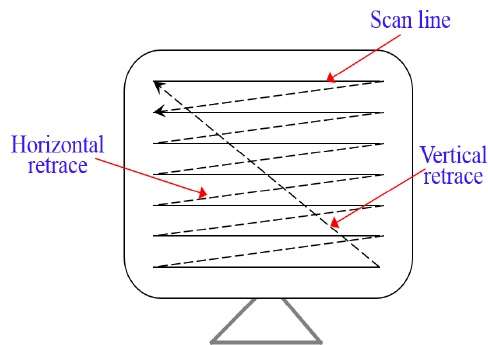
랜덤 스캔 (벡터 스캔)
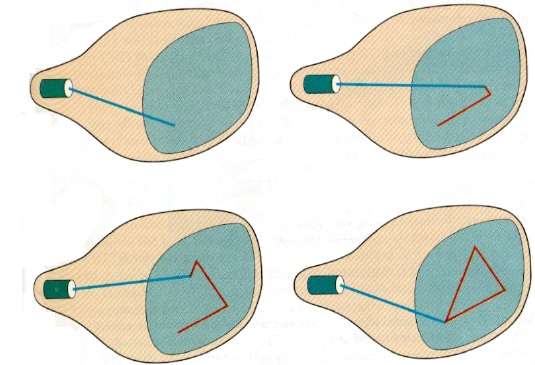
이 기술에서 전자빔은 래스터 스캔에서와 같이 왼쪽에서 오른쪽으로, 위에서 아래로 스캔하는 대신 그림이 그려지는 화면 부분에만 향합니다. 그것은 또한 불린다vector display, stroke-writing display, 또는 calligraphic display.
그림 정의는 메모리 영역에 선 그리기 명령 집합으로 저장됩니다. refresh display file. 지정된 그림을 표시하기 위해 시스템은 표시 파일에있는 명령 세트를 순환하면서 각 구성 요소 라인을 차례로 그립니다. 모든 선 그리기 명령이 처리 된 후 시스템은 목록의 첫 번째 행 명령으로 다시 순환합니다.
랜덤 스캔 디스플레이는 그림의 모든 구성 요소 선을 1 초에 30-60 번 그리도록 설계되었습니다.
컴퓨터 그래픽의 응용
Computer Graphics에는 수많은 응용 프로그램이 있으며 그 중 일부는 아래에 나열되어 있습니다.
Computer graphics user interfaces (GUIs) − 사용자가 컴퓨터와 상호 작용할 수있는 그래픽 마우스 지향 패러다임.
Business presentation graphics − "사진은 천 단어의 가치가 있습니다".
Cartography −지도 그리기.
Weather Maps − 실시간 매핑, 상징적 표현.
Satellite Imaging − 측지 이미지.
Photo Enhancement − 흐릿한 사진을 선명하게합니다.
Medical imaging − MRI, CAT 스캔 등-비 침습적 내부 검사.
Engineering drawings − 기계, 전기, 시민 등-과거의 청사진을 대체합니다.
Typography − 출판시 캐릭터 이미지 사용-과거의 어려운 유형을 대체합니다.
Architecture − 건설 계획, 외관 스케치-과거의 청사진과 손 그림을 대체합니다.
Art − 컴퓨터는 아티스트에게 새로운 매체를 제공합니다.
Training − 비행 시뮬레이터, 컴퓨터 지원 교육 등
Entertainment − 영화 및 게임.
Simulation and modeling − 물리적 모델링 및 제정 대체
선은 두 점을 연결합니다. 그래픽의 기본 요소입니다. 선을 그리려면 선을 그릴 수있는 두 점이 필요합니다. 다음 세 가지 알고리즘에서 선의 한 점을 다음과 같이 참조합니다.$X_{0}, Y_{0}$ 두 번째 선점은 $X_{1}, Y_{1}$.
DDA 알고리즘
디지털 차동 분석기 (DDA) 알고리즘은 여기에서 단계별로 설명하는 간단한 라인 생성 알고리즘입니다.
Step 1 − 두 끝점의 입력 얻기 $(X_{0}, Y_{0})$ 과 $(X_{1}, Y_{1})$.
Step 2 − 두 끝점 간의 차이를 계산합니다.
dx = X1 - X0
dy = Y1 - Y0Step 3− 2 단계에서 계산 된 차이를 기준으로 픽셀을 넣을 단계 수를 식별해야합니다. dx> dy이면 x 좌표에 더 많은 단계가 필요합니다. 그렇지 않으면 y 좌표에서.
if (absolute(dx) > absolute(dy))
Steps = absolute(dx);
else
Steps = absolute(dy);Step 4 − x 좌표와 y 좌표의 증분을 계산합니다.
Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;Step 5 − 그에 따라 x 및 y 좌표를 성공적으로 증가시켜 픽셀을 배치하고 선 그리기를 완료합니다.
for(int v=0; v < Steps; v++)
{
x = x + Xincrement;
y = y + Yincrement;
putpixel(Round(x), Round(y));
}Bresenham의 라인 생성
Bresenham 알고리즘은 또 다른 증분 스캔 변환 알고리즘입니다. 이 알고리즘의 가장 큰 장점은 정수 계산 만 사용한다는 것입니다. 단위 간격으로 x 축을 가로 질러 이동하고 각 단계에서 두 개의 서로 다른 y 좌표 중에서 선택합니다.
예를 들어, 다음 그림과 같이 위치 (2, 3)에서 (3, 3) 및 (3, 4) 중에서 선택해야합니다. 원래 선에 더 가까운 점을 원합니다.
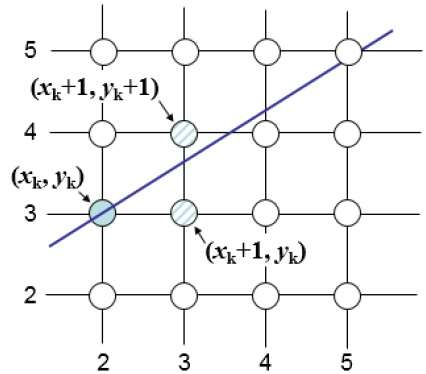
샘플 위치에서 $X_{k}+1,$ 수학적 선과의 수직 분리는 다음과 같이 표시됩니다. $d_{upper}$ 과 $d_{lower}$.
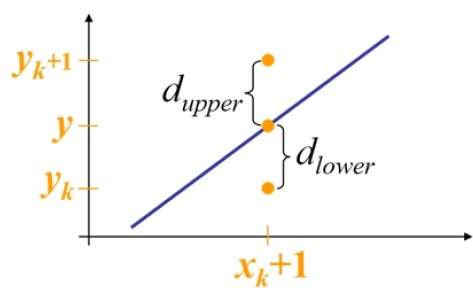
위의 그림에서 수학 라인의 y 좌표는 $x_{k}+1$ -
Y = m ($X_{k}$+1) + b
그래서, $d_{upper}$ 과 $d_{lower}$ 다음과 같이 주어진다-
$$d_{lower} = y-y_{k}$$
$$= m(X_{k} + 1) + b - Y_{k}$$
과
$$d_{upper} = (y_{k} + 1) - y$$
$= Y_{k} + 1 - m (X_{k} + 1) - b$
이를 사용하여 어떤 픽셀이 수학적 선에 더 가까운 지에 대한 간단한 결정을 내릴 수 있습니다. 이 간단한 결정은 두 픽셀 위치의 차이를 기반으로합니다.
$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$
m 을 dy / dx 로 대체하겠습니다. 여기서 dx 와 dy 는 끝점 간의 차이입니다.
$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
따라서 결정 매개 변수 $P_{k}$선을 따라 k 번째 단계에 대해 다음 과 같이 지정됩니다.
$$p_{k} = dx(d_{lower} - d_{upper})$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
결정 매개 변수의 부호 $P_{k}$ 의 그것과 동일합니다 $d_{lower} - d_{upper}$.
만약 $p_{k}$ 음수이면 아래쪽 픽셀을 선택하고 그렇지 않으면 위쪽 픽셀을 선택합니다.
좌표 변경은 단위 단계에서 x 축을 따라 발생하므로 정수 계산으로 모든 작업을 수행 할 수 있습니다. 단계 k + 1에서 결정 매개 변수는 다음과 같이 주어집니다.
$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$
빼기 $p_{k}$ 이것으로부터 우리는-
$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$
그러나, $x_{k+1}$ 와 같다 $x_{k+1}$. 그래서-
$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$
어디, $Y_{k+1} – Y_{k}$ 기호에 따라 0 또는 1입니다. $P_{k}$.
첫 번째 결정 매개 변수 $p_{0}$ 평가됩니다 $(x_{0}, y_{0})$ 다음과 같이 주어집니다-
$$p_{0} = 2dy - dx$$
이제 위의 모든 점과 계산을 염두에두고 기울기 m <1에 대한 Bresenham 알고리즘이 있습니다.
Step 1 − 라인의 두 끝점을 입력하고 왼쪽 끝점을 $(x_{0}, y_{0})$.
Step 2 − 포인트 플로팅 $(x_{0}, y_{0})$.
Step 3 − 상수 dx, dy, 2dy 및 (2dy – 2dx)를 계산하고 결정 매개 변수에 대한 첫 번째 값을 다음과 같이 구합니다.
$$p_{0} = 2dy - dx$$
Step 4 − 각각 $X_{k}$ k = 0에서 시작하는 선을 따라 다음 테스트를 수행하십시오.
만약 $p_{k}$ <0, 플롯 할 다음 점은 $(x_{k}+1, y_{k})$ 과
$$p_{k+1} = p_{k} + 2dy$$ 그렇지 않으면,
$$(x_{k}, y_{k}+1)$$
$$p_{k+1} = p_{k} + 2dy - 2dx$$
Step 5 − 4 단계 (dx – 1)를 반복합니다.
m> 1의 경우, 매번 y를 증가시키면서 x를 증가시켜야하는지 확인하십시오.
해결 후 결정 매개 변수에 대한 방정식 $P_{k}$ 매우 유사 할 것입니다. 방정식의 x와 y 만 서로 바뀝니다.
중간 점 알고리즘
중간 점 알고리즘은 Pitteway와 Van Aken이 수정 한 Bresenham 때문입니다. 다음 그림과 같이 점 P를 (x, y) 좌표에 이미 놓고 선의 기울기가 0 ≤ k ≤ 1이라고 가정합니다.
이제 다음 점을 E 또는 N에 배치할지 여부를 결정해야합니다. 이것은 점 N 또는 E에 가장 가까운 교차점 Q를 식별하여 선택할 수 있습니다. 교차점 Q가 점 N에 가장 가까운 경우 N은 다음과 같이 간주됩니다. 다음 요점; 그렇지 않으면 E.
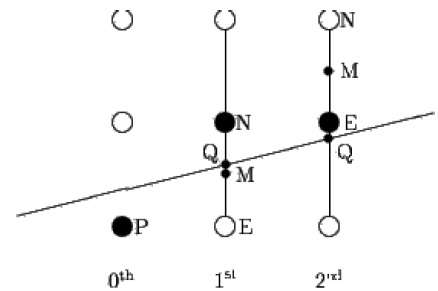
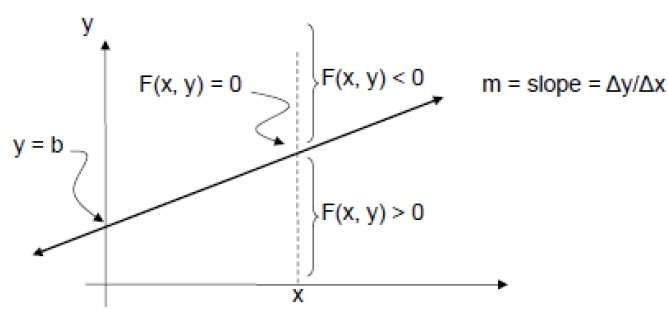
이를 확인하려면 먼저 중간 점 M (x + 1, y + ½)을 계산합니다. E와 N을 연결하는 수직선이있는 선의 교차점 Q가 M 미만이면 E를 다음 점으로 취합니다. 그렇지 않으면 N을 다음 점으로 취하십시오.
이를 확인하기 위해 암시 적 방정식을 고려해야합니다.
F (x, y) = mx + b-y
주어진 X에서 양의 m에 대해,
- y가 라인에 있으면 F (x, y) = 0
- y가 선 위에 있으면 F (x, y) <0
- y가 선 아래에 있으면 F (x, y)> 0
화면에 원을 그리는 것은 선을 그리는 것보다 조금 복잡합니다. 원을 생성하는 두 가지 인기있는 알고리즘이 있습니다.Bresenham’s Algorithm 과 Midpoint Circle Algorithm. 이러한 알고리즘은 원을 그리는 데 필요한 후속 점을 결정한다는 아이디어를 기반으로합니다. 알고리즘에 대해 자세히 논의 해 보겠습니다.
원의 방정식은 $X^{2} + Y^{2} = r^{2},$ 여기서 r은 반경입니다.
Bresenham의 알고리즘
래스터 표시에 연속 호를 표시 할 수 없습니다. 대신 호를 완성하기 위해 가장 가까운 픽셀 위치를 선택해야합니다.
다음 그림에서 픽셀을 (X, Y) 위치에 배치했으며 이제 N (X + 1, Y) 또는 S (X + 1)에 다음 픽셀을 배치 할 위치를 결정해야합니다. Y-1).
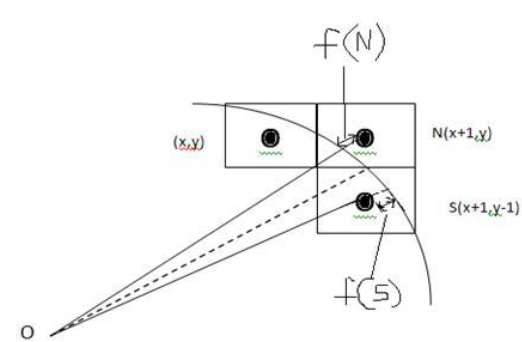
이는 결정 매개 변수에 의해 결정될 수 있습니다. d.
- d <= 0이면 N (X + 1, Y)이 다음 픽셀로 선택됩니다.
- d> 0이면 S (X + 1, Y-1)가 다음 픽셀로 선택됩니다.
연산
Step 1− 원과 반경의 중심 좌표를 구하여 각각 x, y, R에 저장합니다. P = 0 및 Q = R을 설정합니다.
Step 2 − 결정 매개 변수 D = 3 – 2R을 설정합니다.
Step 3 − P ≤ Q 동안 8 단계를 반복합니다.
Step 4 − Draw Circle (X, Y, P, Q)을 호출합니다.
Step 5 − P 값을 증가시킵니다.
Step 6 − D <0이면 D = D + 4P + 6.
Step 7 − 그렇지 않으면 R = R-1, D = D + 4 (PQ) + 10을 설정합니다.
Step 8 − Draw Circle (X, Y, P, Q)을 호출합니다.
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).중간 점 알고리즘
Step 1 − 입력 반경 r 및 원 중심 $(x_{c,} y_{c})$ 원점을 중심으로 한 원의 원주에 대한 첫 번째 점을 다음과 같이 구합니다.
(x0, y0) = (0, r)Step 2 − 결정 매개 변수의 초기 값을 다음과 같이 계산합니다.
$P_{0}$ = 5/4 – r (이 방정식의 단순화를 위해 다음 설명을 참조하십시오.)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0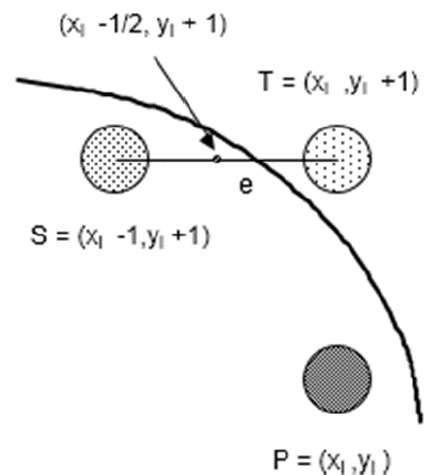
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 − 각각 $X_{K}$ K = 0에서 시작하는 위치, 다음 테스트 수행-
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
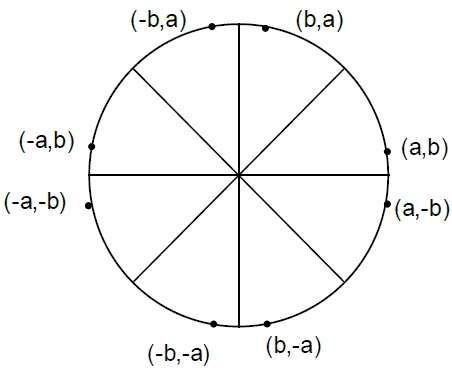
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 − 다른 7 개의 8 분원에서 대칭점을 결정합니다.
Step 5 − 각 계산 픽셀 위치 (X, Y)를 중앙에있는 원형 경로로 이동 $(X_{C,} Y_{C})$ 좌표 값을 플로팅합니다.
X = X + XC, Y = Y + YCStep 6 − X> = Y가 될 때까지 3-5 단계를 반복합니다.
다각형은 다음 그림과 같이 정렬 된 정점 목록입니다. 폴리곤을 특정 색상으로 채우려면 폴리곤의 경계에있는 픽셀과 폴리곤 내부에있는 픽셀을 결정해야합니다. 이 장에서는 다양한 기술을 사용하여 다각형을 채우는 방법을 알아 봅니다.

스캔 라인 알고리즘
이 알고리즘은 스캔 라인을 다각형 가장자리와 교차하여 작동하고 교차 쌍 사이의 다각형을 채 웁니다. 다음 단계는이 알고리즘의 작동 방식을 보여줍니다.
Step 1 − 주어진 다각형에서 Ymin과 Ymax를 찾으십시오.
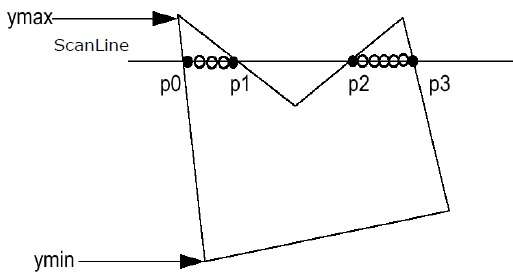
Step 2− ScanLine은 Ymin에서 Ymax까지 다각형의 각 가장자리와 교차합니다. 다각형의 각 교차점에 이름을 지정합니다. 위에 표시된 그림에 따라 p0, p1, p2, p3으로 이름이 지정됩니다.
Step 3 − X 좌표의 오름차순으로 교차점을 정렬합니다. 즉 (p0, p1), (p1, p2) 및 (p2, p3).
Step 4 − 다각형 내부에있는 모든 좌표 쌍을 채우고 대체 쌍을 무시합니다.
채우기 알고리즘
때때로 우리는 영역과 경계를 다른 색으로 채우려는 물체를 발견합니다. 경계 채우기 알고리즘에서와 같이 특정 경계 색상을 검색하는 대신 지정된 내부 색상으로 이러한 개체를 칠할 수 있습니다.
개체의 경계에 의존하는 대신 채우기 색상에 의존합니다. 즉, 개체의 내부 색상을 채우기 색상으로 대체합니다. 원래 내부 색상의 픽셀이 더 이상 존재하지 않으면 알고리즘이 완료됩니다.
다시 한 번,이 알고리즘은 픽셀을 채우는 4- 연결 또는 8- 연결 방법에 의존합니다. 그러나 경계 색상을 찾는 대신 내부의 일부인 인접한 모든 픽셀을 찾습니다.
경계 채우기 알고리즘
경계 채우기 알고리즘은 이름으로 작동합니다. 이 알고리즘은 객체 내부의 점을 선택하고 객체의 경계에 도달 할 때까지 채우기 시작합니다. 이 알고리즘이 작동하려면 경계의 색상과 채울 색상이 달라야합니다.
이 알고리즘에서는 경계의 색상이 전체 개체에 대해 동일하다고 가정합니다. 경계 채우기 알고리즘은 4 개 연결 픽셀 또는 8 개 연결 픽셀로 구현할 수 있습니다.
4- 연결 다각형
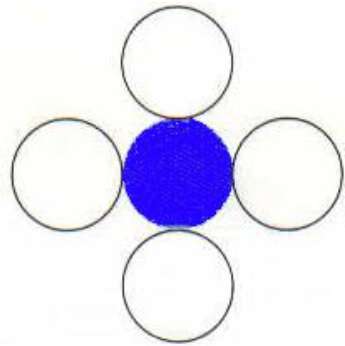
이 기술에서는 그림과 같이 4 개의 연결된 픽셀이 사용됩니다. 현재 픽셀의 위, 아래, 오른쪽 및 왼쪽에 픽셀을 배치하고이 프로세스는 다른 색상의 경계를 찾을 때까지 계속됩니다.
연산
Step 1 − 시드 포인트 (seedx, seedy), fcolor 및 dcol의 값을 초기화합니다.
Step 2 − 다각형의 경계 값을 정의합니다.
Step 3 − 현재 시드 포인트가 기본 색상인지 확인한 다음 경계 픽셀에 도달 할 때까지 4 단계와 5 단계를 반복합니다.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 − 시드 포인트의 채우기 색상으로 기본 색상을 변경합니다.
setPixel(seedx, seedy, fcol)Step 5 − 4 개의 인접 지점으로 절차를 반복적으로 따릅니다.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 − 종료
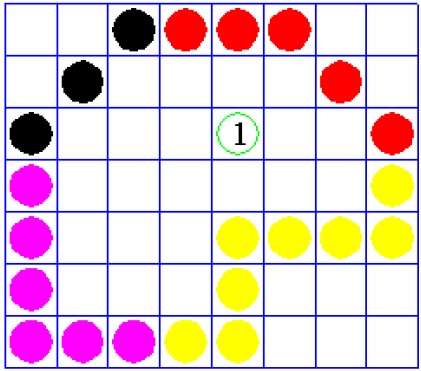
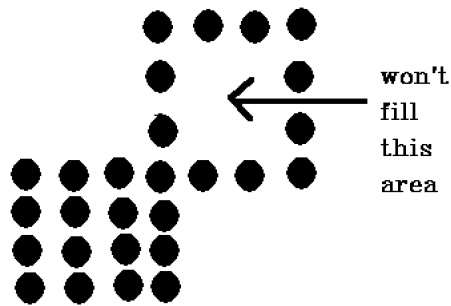
이 기술에 문제가 있습니다. 우리가 전체 지역을 채우려 고 시도한 아래와 같은 경우를 고려하십시오. 여기에서는 이미지가 부분적으로 만 채워집니다. 이러한 경우 4 개 연결 픽셀 기술을 사용할 수 없습니다.
8 개 연결 다각형
이 기술에서는 그림과 같이 8 개의 연결된 픽셀이 사용됩니다. 우리는 4- 연결 기술에서했던 것처럼 현재 픽셀의 위, 아래, 오른쪽 및 왼쪽에 픽셀을 배치합니다.
이 외에도 현재 픽셀의 전체 영역을 덮도록 픽셀을 대각선으로 배치합니다. 이 과정은 다른 색의 경계를 찾을 때까지 계속됩니다.

연산
Step 1 − 시드 포인트 (seedx, seedy), fcolor 및 dcol의 값을 초기화합니다.
Step 2 − 다각형의 경계 값을 정의합니다.
Step 3 − 현재 시드 포인트가 기본 색상인지 확인한 다음 경계 픽셀에 도달 할 때까지 4 단계와 5 단계를 반복합니다.
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 − 시드 포인트의 채우기 색상으로 기본 색상을 변경합니다.
setPixel(seedx, seedy, fcol)Step 5 − 4 개의 인접 지점으로 절차를 반복적으로 따르십시오.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 − 종료
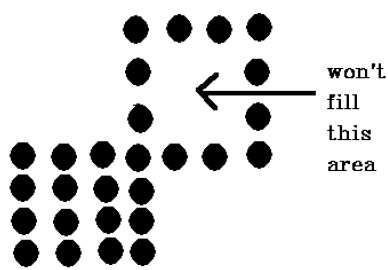
4 연결 픽셀 기술은 8 연결 기술에서는 발생하지 않는 다음 그림과 같이 영역을 채우지 못했습니다.
내부-외부 테스트
이 방법은 다음과 같이 알려져 있습니다. counting number method. 개체를 채우는 동안 특정 지점이 개체 내부에 있는지 외부에 있는지 식별해야하는 경우가 많습니다. 특정 지점이 개체 내부에 있는지 외부에 있는지 식별 할 수있는 두 가지 방법이 있습니다.
- 홀수 짝수 규칙
- 0이 아닌 권선 수 규칙
홀수 짝수 규칙
이 기술에서는 모든 점 (x, y)에서 무한대까지 선을 따라 교차하는 가장자리를 계산합니다. 상호 작용 수가 홀수이면 점 (x, y)은 내부 점입니다. 상호 작용의 수가 짝수이면 점 (x, y)는 외부 점입니다. 다음은 명확한 아이디어를 제공하는 예입니다.
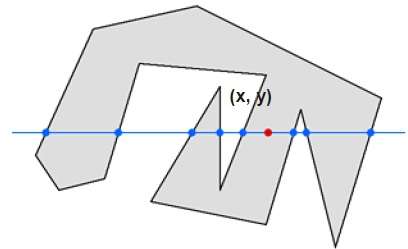
위의 그림에서 (x, y) 지점에서 왼쪽의 상호 작용 지점 수가 5 개이고 오른쪽의 상호 작용 지점 수가 3 개임을 알 수 있습니다. 따라서 총 상호 작용 지점 수는 8입니다. . 따라서 점은 객체 내에서 고려됩니다.
0이 아닌 권선 번호 규칙
이 방법은 또한 주어진 포인트가 내부인지 아닌지를 테스트하기 위해 단순 다각형과 함께 사용됩니다. 핀과 고무 밴드의 도움으로 간단하게 이해할 수 있습니다. 다각형 가장자리 중 하나에 핀을 고정하고 그 안에 고무 밴드를 묶은 다음 다각형 가장자리를 따라 고무 밴드를 늘립니다.
다각형의 모든 가장자리가 고무줄로 덮여 있으면 테스트 할 지점에 고정 된 핀을 확인합니다. 지점에서 바람이 하나 이상 발견되면 다각형 내에서 고려합니다. 그렇지 않으면 지점이 다각형 내부에 없다고 말할 수 있습니다.
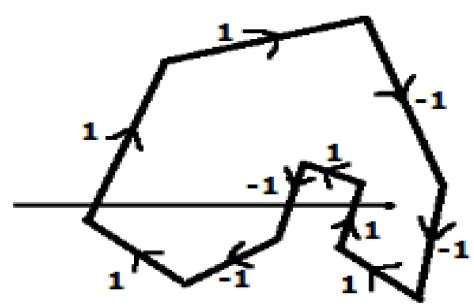
또 다른 방법으로 다각형의 모든 가장자리에 방향을 제공합니다. 테스트 할 지점에서 X 방향의 가장 왼쪽을 향해 스캔 라인을 그립니다.
위쪽으로 향하는 모든 가장자리에 값 1을 지정하고 방향 값으로 다른 모든 -1을 지정합니다.
스캔 라인이 통과하는 가장자리 방향 값을 확인하고 합산합니다.
이 방향 값의 총합이 0이 아니면 테스트 할이 점은 interior point, 그렇지 않으면 exterior point.
위의 그림에서 스캔 라인이 지나가는 방향 값을 합산하면 합계가 1 – 1 + 1 = 1입니다. 0이 아닙니다. 그래서 포인트는 내부 포인트라고합니다.
컴퓨터 그래픽에서 클리핑의 주된 용도는보기 창 밖에있는 개체, 선 또는 선 세그먼트를 제거하는 것입니다. 보기 변환은보기 볼륨 (특히 뷰어 뒤의 지점)에 상대적인 지점의 위치에 민감하지 않으며보기를 생성하기 전에 이러한 지점을 제거해야합니다.
포인트 클리핑
주어진 창에서 점을 자르는 것은 매우 쉽습니다. 직사각형이 창을 나타내는 다음 그림을 고려하십시오. 포인트 클리핑은 주어진 포인트 (X, Y)가 주어진 윈도우 내에 있는지 여부를 알려줍니다. 창의 최소 및 최대 좌표를 사용할지 여부를 결정합니다.
X가 Wx1 ≤ X ≤ Wx2 사이에있는 경우 주어진 점의 X 좌표는 창 내부에 있습니다. 같은 방식으로 Y가 Wy1 ≤ Y ≤ Wy2 사이에 있으면 주어진 지점의 Y 좌표가 창 안에 있습니다.

라인 클리핑
라인 클리핑의 개념은 포인트 클리핑과 동일합니다. 선 자르기에서는 창 밖에있는 선 부분을 잘라 내고 창 안쪽에있는 부분 만 유지합니다.
Cohen-Sutherland 라인 클리핑
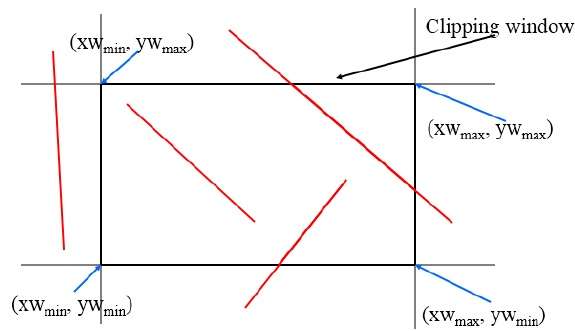
이 알고리즘은 다음 그림과 같이 클리핑 창을 사용합니다. 클리핑 영역의 최소 좌표는 다음과 같습니다.$(XW_{min,} YW_{min})$ 클리핑 영역의 최대 좌표는 $(XW_{max,} YW_{max})$.
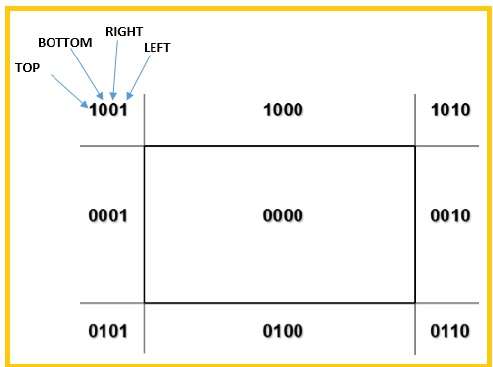
4 비트를 사용하여 전체 영역을 나눕니다. 이 4 비트는 다음 그림과 같이 영역의 상단, 하단, 오른쪽 및 왼쪽을 나타냅니다. 여기,TOP 과 LEFT 비트는 1로 설정됩니다. TOP-LEFT 모서리.
라인에는 3 가지 가능성이 있습니다.
선은 창 안에 완전히 들어갈 수 있습니다 (이 선은 허용되어야 함).
선은 완전히 창 밖에있을 수 있습니다 (이 선은 영역에서 완전히 제거됩니다).
선은 부분적으로 창 내부에있을 수 있습니다 (교차점을 찾고 영역 내부에있는 선 부분 만 그립니다).
연산
Step 1 − 각 엔드 포인트에 지역 코드를 할당합니다.
Step 2 − 두 끝점에 지역 코드가있는 경우 0000 그런 다음이 줄을 수락하십시오.
Step 3 − 그렇지 않으면 논리를 수행합니다. AND두 지역 코드에 대한 작업.
Step 3.1 − 결과가 아닌 경우 0000, 그런 다음 라인을 거부하십시오.
Step 3.2 − 그렇지 않으면 클리핑이 필요합니다.
Step 3.2.1 − 창 밖에있는 선의 끝점을 선택합니다.
Step 3.2.2 − 창 경계에서 교차점을 찾습니다 (지역 코드 기준).
Step 3.2.3 − 끝점을 교차점으로 교체하고 지역 코드를 업데이트하십시오.
Step 3.2.4 − 사소하게 허용되거나 사소하게 거부 된 잘린 선을 찾을 때까지 2 단계를 반복합니다.
Step 4 − 다른 라인에 대해 1 단계를 반복합니다.
Cyrus-Beck 라인 클리핑 알고리즘
이 알고리즘은 Cohen-Sutherland 알고리즘보다 효율적입니다. 파라 메트릭 라인 표현과 단순한 내적을 사용합니다.
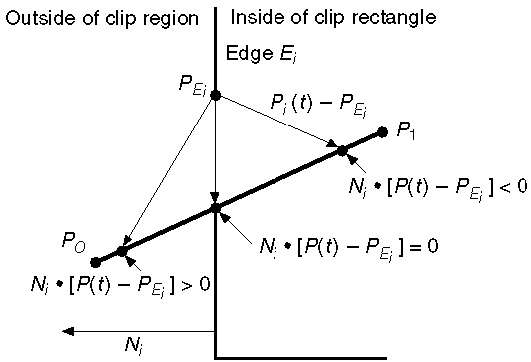
선의 파라 메트릭 방정식은-
P0P1:P(t) = P0 + t(P1-P0)N i를 바깥 쪽 법선 모서리 E i로 둡니다 . 이제 가장자리 E i 에서 임의의 점 P Ei 를 선택한 다음 내적 N i ∙ [P (t) – P Ei ]는 점 P (t)가 클립 가장자리 "내부"인지 아니면 "외부"인지 결정합니다. 클립 가장자리 "위".
N i . [P (t) – P Ei ] <0이면 점 P (t)는 내부에 있습니다.
N i . [P (t) – P Ei ]> 0이면 점 P (t)는 외부에 있습니다.
N i . [P (t) – P Ei ] = 0 (교차점) 인 경우 점 P (t)는 모서리에 있습니다.
N i . [P (t) – P Ei ] = 0
N i . [P 0 + t (P 1 -P 0 ) – P Ei ] = 0 (P (t)를 P 0 + t (P 1 -P 0 )로 대체 )
N i . [P 0 – P Ei ] + N i .t [P 1 -P 0 ] = 0
N i . [P 0 – P Ei ] + N i ∙ tD = 0 ([P 1 -P 0 ]을 D로 대체 )
N i . [P 0 – P Ei ] =-N i ∙ tD
t에 대한 방정식은 다음과 같습니다.
$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$
다음 조건에서 유효합니다-
- N i ≠ 0 (오류 발생 불가)
- D ≠ 0 (P 1 ≠ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1 이 E i 와 평행하지 않음 )
다각형 클리핑 (Sutherland Hodgman 알고리즘)
클리핑 창을 지정하여 다각형을자를 수도 있습니다. Sutherland Hodgeman 다각형 클리핑 알고리즘은 다각형 클리핑에 사용됩니다. 이 알고리즘에서는 다각형의 모든 정점이 클리핑 창의 각 가장자리에 대해 잘립니다.
먼저 다각형의 새 정점을 얻기 위해 다각형 창의 왼쪽 가장자리에 대해 다각형이 잘립니다. 이 새 정점은 다음 그림과 같이 클리핑 창의 오른쪽 가장자리, 위쪽 가장자리, 아래쪽 가장자리에 대해 다각형을 자르는 데 사용됩니다.
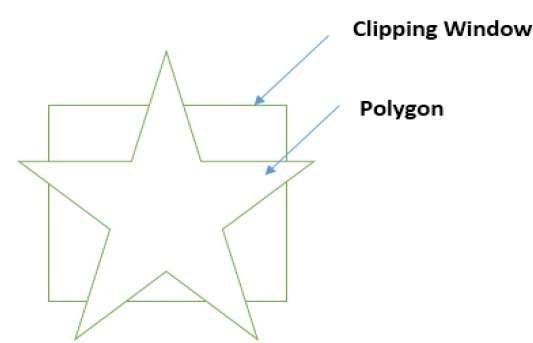
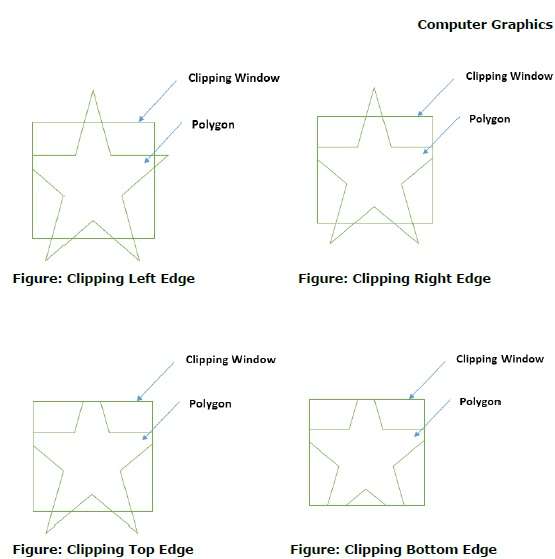
클리핑 창으로 다각형의 가장자리를 처리하는 동안 가장자리가 완전히 클리핑 창 내부에 있지 않고 교차점에서 외부 가장자리까지의 일부 가장자리가 잘 리면 교차점이 발견됩니다. 다음 그림은 왼쪽, 오른쪽, 위쪽 및 아래쪽 가장자리 클리핑을 보여줍니다.
텍스트 클리핑
컴퓨터 그래픽에서 텍스트 클리핑을 제공하기 위해 다양한 기술이 사용됩니다. 문자를 생성하는 데 사용되는 방법과 특정 응용 프로그램의 요구 사항에 따라 다릅니다. 아래에 나열된 텍스트 클리핑에 대한 세 가지 방법이 있습니다.
- 전체 또는 없음 문자열 클리핑
- 전체 또는 없음 문자 클리핑
- 텍스트 클리핑
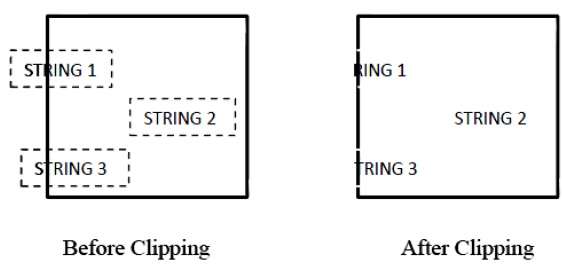
다음 그림은 모든 문자열 클리핑을 보여줍니다.
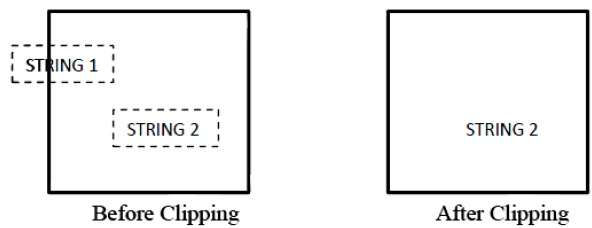
전체 또는 없음 문자열 클리핑 방법에서 전체 문자열을 유지하거나 클리핑 창을 기반으로 전체 문자열을 거부합니다. 위의 그림에서 볼 수 있듯이 STRING2는 완전히 클리핑 창 안에 있으므로 유지하고 STRING1은 부분적으로 창 안에 만 있으면 거부합니다.
다음 그림은 모든 문자 클리핑을 보여줍니다.
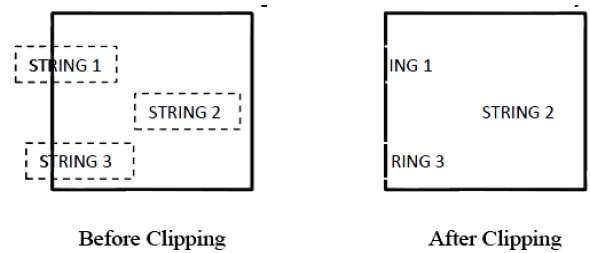
이 클리핑 방법은 전체 문자열이 아닌 문자를 기반으로합니다. 이 메서드에서 문자열이 완전히 클리핑 창 안에 있으면 그대로 유지합니다. 부분적으로 창 밖에 있으면-
외부에있는 문자열 부분 만 거부합니다.
문자가 클리핑 창의 경계에 있으면 전체 문자를 버리고 나머지 문자열을 유지합니다.
다음 그림은 텍스트 클리핑을 보여줍니다.
이 클리핑 방법은 전체 문자열이 아닌 문자를 기반으로합니다. 이 메서드에서 문자열이 완전히 클리핑 창 안에 있으면 그대로 유지합니다. 부분적으로 창 밖에 있으면
외부에있는 문자열 부분 만 거부합니다.
캐릭터가 클리핑 윈도우의 경계에 있으면 클리핑 윈도우 밖에있는 캐릭터 부분 만 버립니다.
비트 맵 그래픽
비트 맵은 이미지를 설명하는 픽셀 모음입니다. 컴퓨터가 사진을 저장하고 표시하는 데 사용하는 컴퓨터 그래픽 유형입니다. 이러한 유형의 그래픽에서 이미지는 비트별로 저장되므로 비트 맵 그래픽이라고합니다. 더 나은 이해를 위해 비트 맵 그래픽을 사용하여 웃는 얼굴을 그리는 다음 예제를 고려해 보겠습니다.

이제이 웃는 얼굴이 컴퓨터 그래픽에 어떻게 저장되는지 살펴 보겠습니다.
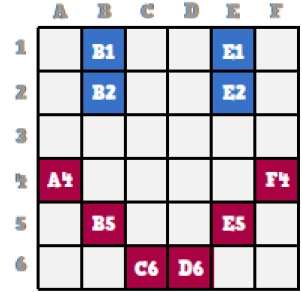
원래 웃는 얼굴을 면밀히 관찰하면 위 그림에서 B1, B2, E1, E2로 표시된 두 개의 파란색 선이 있음을 알 수 있습니다.
같은 방식으로 스마일리는 각각 A4, B5, C6, D6, E5 및 F4의 조합 비트를 사용하여 표현됩니다.
비트 맵 그래픽의 주요 단점은-
비트 맵 이미지의 크기를 조정할 수 없습니다. 크기를 조정하려고하면 픽셀이 흐려집니다.
컬러 비트 맵은 매우 클 수 있습니다.
변환은 규칙을 적용하여 일부 그래픽을 다른 것으로 변경하는 것을 의미합니다. 변환, 확대 / 축소, 회전, 기울이기 등과 같은 다양한 유형의 변환이있을 수 있습니다. 변환이 2D 평면에서 발생하는 것을 2D 변환이라고합니다.
변환은 컴퓨터 그래픽에서 화면의 그래픽 위치를 변경하고 크기 나 방향을 변경하는 데 중요한 역할을합니다.
동종 좌표
평행 이동과 회전 및 크기 조정과 같은 일련의 변환을 수행하려면 순차적 프로세스를 따라야합니다.
- 좌표를 번역하고,
- 변환 된 좌표를 회전 한 다음
- 회전 된 좌표를 조정하여 합성 변환을 완료합니다.
이 과정을 단축하려면 2x2 변환 행렬 대신 3x3 변환 행렬을 사용해야합니다. 2x2 행렬을 3x3 행렬로 변환하려면 추가 더미 좌표 W를 추가해야합니다.
이런 식으로 점을 2 개의 숫자 대신 3 개의 숫자로 표현할 수 있습니다. Homogenous Coordinate체계. 이 시스템에서 모든 변환 방정식을 행렬 곱셈으로 나타낼 수 있습니다. 모든 데카르트 점 P (X, Y)는 P '(X h , Y h , h)에 의해 동종 좌표로 변환 될 수 있습니다 .
번역
번역은 개체를 화면의 다른 위치로 이동합니다. 변환 좌표 (t x , t y )를 원래 좌표 (X, Y)에 추가하여 새 좌표 (X ', Y')를 가져와 2D로 점을 변환 할 수 있습니다 .
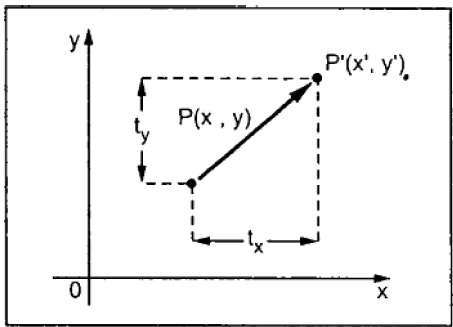
위의 그림에서 다음과 같이 쓸 수 있습니다.
X’ = X + tx
Y’ = Y + ty
쌍 (t x , t y )을 변환 벡터 또는 시프트 벡터라고합니다. 위의 방정식은 열 벡터를 사용하여 나타낼 수도 있습니다.
$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$
우리는 그것을 다음과 같이 쓸 수 있습니다.
P’ = P + T
회전
회전에서는 원점에서 특정 각도 θ (세타)로 물체를 회전합니다. 다음 그림에서 점 P (X, Y)가 원점에서 거리 r과 함께 수평 X 좌표에서 각도 φ에 위치 함을 알 수 있습니다.
각도 θ로 회전한다고 가정 해 봅시다. 새 위치로 회전하면 새 점 P '(X', Y ')가 생성됩니다.

표준 삼각법을 사용하여 점 P (X, Y)의 원래 좌표는 다음과 같이 나타낼 수 있습니다.
$X = r \, cos \, \phi ...... (1)$
$Y = r \, sin \, \phi ...... (2)$
같은 방식으로 점 P '(X', Y ')를 다음과 같이 표현할 수 있습니다.
${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$
${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$
(3)과 (4)에서 방정식 (1)과 (2)를 각각 대입하면
${x}'= x \: cos \: \theta − \: y \: sin \: \theta $
${y}'= x \: sin \: \theta + \: y \: cos \: \theta $
위의 방정식을 행렬 형태로 표현하면,
$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$
P '= P ∙ R
여기서 R은 회전 행렬입니다.
$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$
회전 각도는 양수 및 음수 일 수 있습니다.
양의 회전 각도의 경우 위의 회전 행렬을 사용할 수 있습니다. 그러나 음의 각도 회전의 경우 매트릭스는 아래와 같이 변경됩니다.
$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$
$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$
스케일링
개체의 크기를 변경하려면 크기 조정 변환이 사용됩니다. 크기 조정 프로세스에서 개체의 크기를 확장하거나 압축합니다. 원하는 결과를 얻기 위해 개체의 원래 좌표에 배율 인수를 곱하여 배율을 조정할 수 있습니다.
원래 좌표가 (X, Y)이고 배율 인수가 (S X , S Y )이고 생성 된 좌표가 (X ', Y') 라고 가정 해 보겠습니다 . 이것은 아래와 같이 수학적으로 표현 될 수 있습니다.
X' = X . SX and Y' = Y . SY
배율 계수 S X , S Y 는 각각 X 및 Y 방향으로 개체의 배율을 조정합니다. 위의 방정식은 다음과 같이 행렬 형태로도 표현할 수 있습니다.
$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$
또는
P’ = P . S
여기서 S는 스케일링 행렬입니다. 확장 프로세스는 다음 그림에 나와 있습니다.
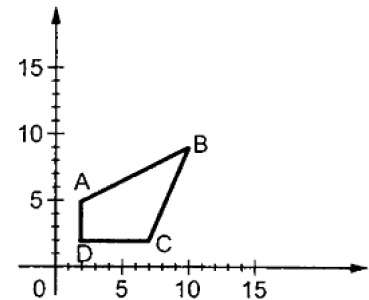
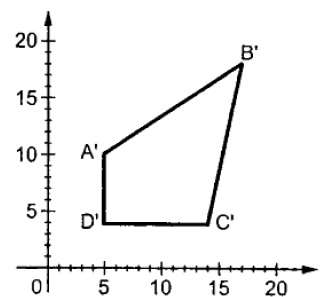
스케일링 계수 S에 1보다 작은 값을 제공하면 객체의 크기를 줄일 수 있습니다. 1보다 큰 값을 제공하면 개체의 크기를 늘릴 수 있습니다.
반사
반사는 원래 물체의 거울 이미지입니다. 즉, 180 ° 회전 동작이라고 할 수 있습니다. 반사 변환에서 개체의 크기는 변경되지 않습니다.
다음 그림은 각각 X 및 Y 축과 원점에 대한 반사를 보여줍니다.
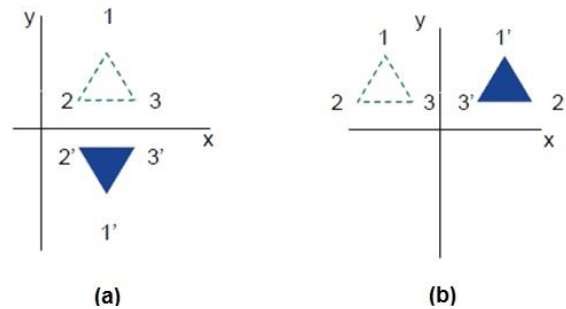
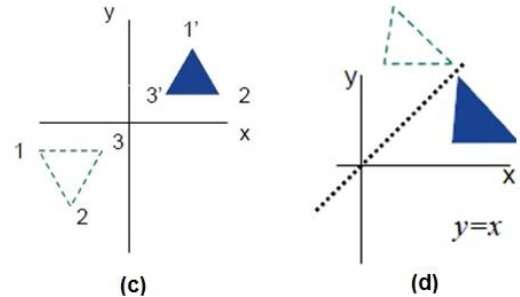
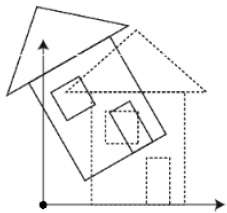
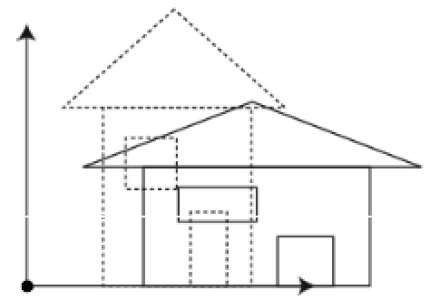
전단
물체의 모양을 기울이는 변형을 전단 변형이라고합니다. 두 가지 전단 변환이 있습니다.X-Shear 과 Y-Shear. 하나는 X 좌표 값을 이동하고 다른 하나는 Y 좌표 값을 이동합니다. 하나; 두 경우 모두 하나의 좌표 만 해당 좌표를 변경하고 다른 좌표는 해당 값을 유지합니다. 전단은 또한Skewing.
X-Shear
X-Shear는 Y 좌표를 유지하고 X 좌표가 변경되어 아래 그림과 같이 수직선이 오른쪽 또는 왼쪽으로 기울어집니다.
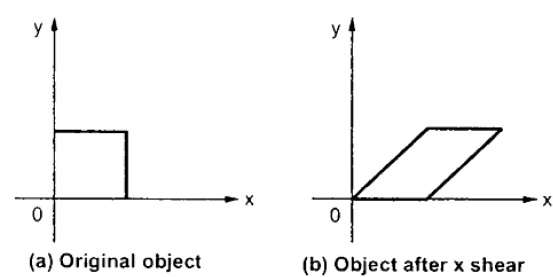
X-Shear에 대한 변환 행렬은 다음과 같이 나타낼 수 있습니다.
$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
Y '= Y + Sh y . 엑스
X '= X
Y 전단
Y-Shear는 X 좌표를 유지하고 Y 좌표를 변경하여 다음 그림과 같이 수평선이 위아래로 기울어지는 선으로 변환되도록합니다.
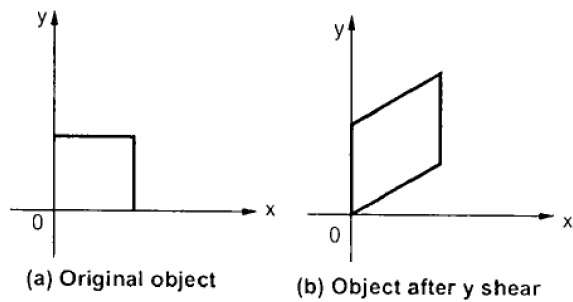
Y-Shear는 다음과 같이 행렬로 표현 될 수 있습니다.
$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
X '= X + Sh x . 와이
Y '= Y
복합 변환
평면 T1의 변환 후 제 2 평면 변환 T2가 뒤 따르면 결과 자체는 그 순서대로 취해진 T1 및 T2의 구성 인 단일 변환 T로 표현 될 수 있습니다. T = T1 ∙ T2로 표기됩니다.
복합 변환은 변환 행렬을 연결하여 결합 된 변환 행렬을 얻을 수 있습니다.
결합 된 행렬-
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
여기서 [Ti]는
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
일반적으로 행렬 곱셈이 누적되지 않기 때문에 변환 순서의 변경은 다른 결과를 가져옵니다. 즉 [A]입니다. [B] ≠ [B]. [A]와 곱셈의 순서. 변환을 구성하는 기본 목적은 일련의 변환을 차례로 적용하는 대신 하나의 구성된 변환을 포인트에 적용하여 효율성을 얻는 것입니다.
예를 들어, 임의의 점 (X p , Y p ) 을 중심으로 객체를 회전하려면 세 단계를 수행해야합니다.
- 점 (X p , Y p )을 원점으로 변환합니다.
- 원점을 기준으로 회전합니다.
- 마지막으로 회전 중심을 원래 위치로 되돌립니다.
2D 시스템에서는 두 개의 좌표 X와 Y 만 사용하지만 3D에서는 추가 좌표 Z가 추가됩니다. 3D 그래픽 기술과 그 응용 프로그램은 엔터테인먼트, 게임 및 컴퓨터 지원 디자인 산업의 기본입니다. 과학적 시각화에 대한 지속적인 연구 영역입니다.
또한 3D 그래픽 구성 요소는 이제 거의 모든 개인용 컴퓨터의 일부이며, 전통적으로 게임과 같은 그래픽 집약적 인 소프트웨어 용으로 고안되었지만 다른 응용 프로그램에서 점점 더 많이 사용되고 있습니다.
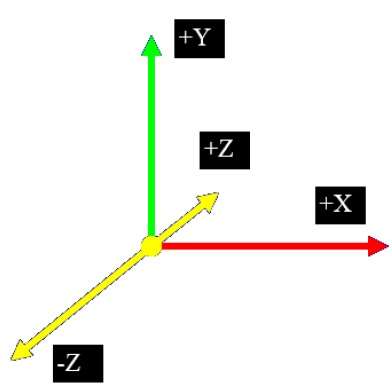
평행 투영
평행 투영은 z 좌표를 버리고 객체의 각 정점에서 평행선이 뷰 평면과 교차 할 때까지 연장됩니다. 평행 투영에서는 투영 중심 대신 투영 방향을 지정합니다.
평행 투영에서 투영 중심에서 투영 평면까지의 거리는 무한합니다. 이 유형의 투영에서는 원래 오브젝트의 연결에 해당하는 선 세그먼트로 투영 된 정점을 연결합니다.
평행 투영은 덜 현실적이지만 정확한 측정에는 좋습니다. 이 유형의 투영에서 평행선은 평행을 유지하고 각도는 유지되지 않습니다. 다양한 유형의 병렬 투영이 다음 계층 구조에 표시됩니다.
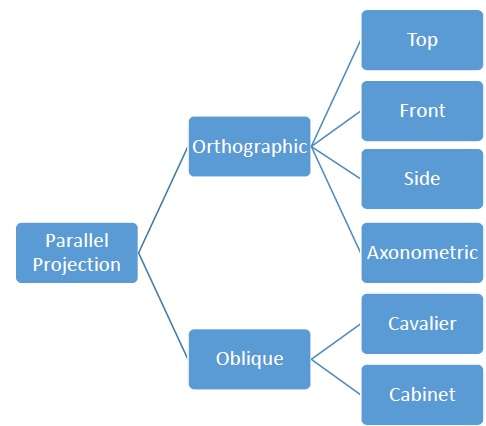
직교 투영
직교 투영에서 투영 방향은 평면 투영에 수직입니다. 세 가지 유형의 직교 투영이 있습니다.
- 전면 프로젝션
- 최고 프로젝션
- 측면 투영
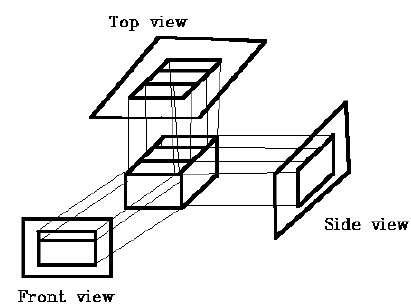
비스듬한 투영
경사 투영에서 투영 방향은 평면 투영에 수직이 아닙니다. 경사 투영에서는 직교 투영보다 물체를 더 잘 볼 수 있습니다.
경사 투영에는 두 가지 유형이 있습니다. Cavalier 과 Cabinet. Cavalier 투영은 투영 평면과 45 ° 각도를 만듭니다. 뷰 평면에 수직 인 선의 투영은 Cavalier 투영의 선 자체와 길이가 같습니다. 무심한 투영에서 세 가지 주요 방향 모두에 대한 단축 계수는 동일합니다.
캐비닛 투영은 투영 평면과 63.4 ° 각도를 만듭니다. 캐비닛 투영에서보기 표면에 수직 인 선은 실제 길이의 ½로 투영됩니다. 두 투영 모두 다음 그림에 나와 있습니다.

등각 투영
물체의 한면 이상을 보여주는 직교 투영을 axonometric orthographic projections. 가장 일반적인 축 방향 투영법은isometric projection투영 평면이 모델 좌표계의 각 좌표 축과 동일한 거리에서 교차합니다. 이 투영에서 선의 평행 성은 유지되지만 각도는 유지되지 않습니다. 다음 그림은 등각 투영을 보여줍니다-

투시 투영
투시 투영에서 투영 중심에서 투영 평면까지의 거리는 한정되어 있으며 물체의 크기는 거리에 따라 반비례하여 더 사실적으로 보입니다.
거리와 각도는 유지되지 않으며 평행선은 평행을 유지하지 않습니다. 대신, 그들은 모두center of projection 또는 projection reference point. 다음 차트에 표시된 3 가지 유형의 투시 투영이 있습니다.
One point 원근 투영은 그리기가 간단합니다.
Two point 원근 투영은 더 나은 깊이 감을 제공합니다.
Three point 원근 투영은 그리기가 가장 어렵습니다.
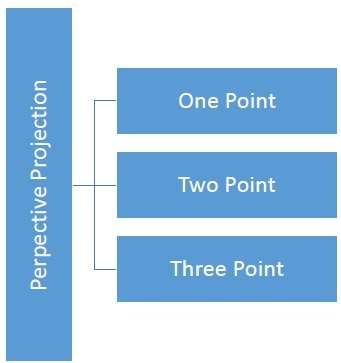
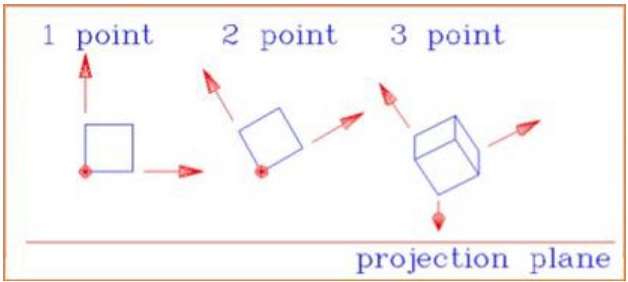
다음 그림은 세 가지 유형의 투시 투영을 모두 보여줍니다.
번역
3D 변환에서는 X 및 Y 좌표와 함께 Z 좌표를 전송합니다. 3D 번역 프로세스는 2D 번역과 유사합니다. 번역은 개체를 화면의 다른 위치로 이동합니다.
다음 그림은 번역의 효과를 보여줍니다-
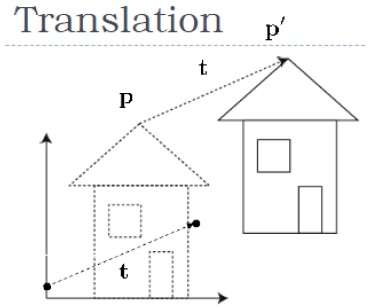
변환 좌표를 추가하여 점을 3D로 변환 할 수 있습니다. $(t_{x,} t_{y,} t_{z})$ 새로운 좌표 (X ', Y', Z ')를 얻기 위해 원래 좌표 (X, Y, Z)로.
$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
P '= P ∙ T
$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$
회전
3D 회전은 2D 회전과 동일하지 않습니다. 3D 회전에서는 회전축과 함께 회전 각도를 지정해야합니다. X, Y, Z 축을 중심으로 3D 회전을 수행 할 수 있습니다. 그들은 아래와 같이 매트릭스 형태로 표현됩니다-
$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$
다음 그림은 다양한 축에 대한 회전을 설명합니다.
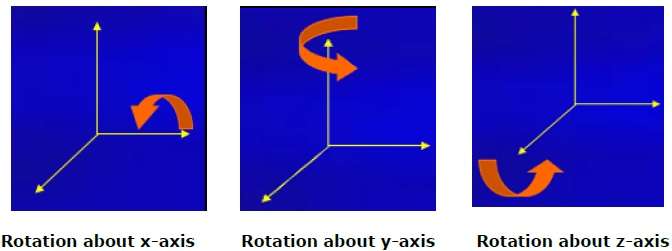
스케일링
크기 조정 변환을 사용하여 개체의 크기를 변경할 수 있습니다. 크기 조정 프로세스에서 개체의 크기를 확장하거나 압축합니다. 원하는 결과를 얻기 위해 개체의 원래 좌표에 배율 인수를 곱하여 배율을 조정할 수 있습니다. 다음 그림은 3D 스케일링의 효과를 보여줍니다.
3D 스케일링 작업에서는 세 개의 좌표가 사용됩니다. 원래 좌표가 (X, Y, Z)이고 배율 인수가$(S_{X,} S_{Y,} S_{z})$각각 생성 된 좌표는 (X ', Y', Z ')입니다. 이것은 아래와 같이 수학적으로 표현 될 수 있습니다.
$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
P '= P ∙ S
$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$
전단
물체의 모양을 기울이는 변형을 shear transformation. 2D 전단과 마찬가지로 3D에서 X 축, Y 축 또는 Z 축을 따라 개체를 전단 할 수 있습니다.
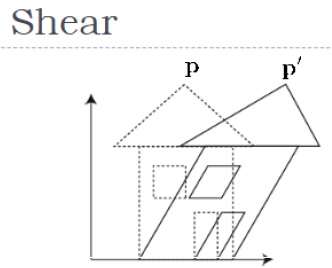
위 그림과 같이 좌표 P가 있습니다.이를 전단하여 새로운 좌표 P '를 얻을 수 있으며, 이는 아래와 같이 3D 매트릭스 형태로 표현 될 수 있습니다.
$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
P '= P ∙ Sh
$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$
$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$
$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$
변환 행렬
변환 매트릭스는 변환을위한 기본 도구입니다. nxm 차원의 행렬은 객체의 좌표와 곱해집니다. 일반적으로 3 x 3 또는 4 x 4 행렬이 변환에 사용됩니다. 예를 들어 다양한 작업에 대해 다음 매트릭스를 고려하십시오.
| $T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$ | $S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$ | $Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Translation Matrix | Scaling Matrix | Shear Matrix |
| $R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Rotation Matrix | ||
컴퓨터 그래픽에서는 종종 화면에 다양한 유형의 개체를 그려야합니다. 개체는 항상 평평하지 않으며 개체를 그리기 위해 곡선을 여러 번 그려야합니다.
곡선 유형
곡선은 무한히 큰 점 집합입니다. 각 점에는 끝점을 제외한 두 개의 이웃이 있습니다. 곡선은 크게 세 가지 범주로 분류 할 수 있습니다.explicit, implicit, 과 parametric curves.
암시 적 곡선
암시 적 곡선 표현은 곡선에 점이 있는지 확인하기 위해 테스트 할 수있는 절차를 사용하여 곡선의 점 집합을 정의합니다. 일반적으로 암시 적 곡선은 다음 형식의 암시 적 함수에 의해 정의됩니다.
f (x, y) = 0
다중 값 곡선 (x 값에 대해 여러 y 값)을 나타낼 수 있습니다. 일반적인 예는 암시 적 표현이 다음과 같은 원입니다.
x2 + y2 - R2 = 0
명시 적 곡선
수학 함수 y = f (x)를 곡선으로 그릴 수 있습니다. 이러한 함수는 곡선의 명시 적 표현입니다. 명시 적 표현은 수직선을 나타낼 수없고 단일 값이기 때문에 일반적이지 않습니다. x의 각 값에 대해 함수는 일반적으로 y의 단일 값만 계산합니다.
파라 메트릭 곡선
파라 메트릭 형태의 커브를 파라 메트릭 커브라고합니다. 명시 적 및 암시 적 곡선 표현은 함수가 알려진 경우에만 사용할 수 있습니다. 실제로는 파라 메트릭 곡선이 사용됩니다. 2 차원 파라 메트릭 곡선의 형태는 다음과 같습니다.
P (t) = f (t), g (t) 또는 P (t) = x (t), y (t)
함수 f와 g는 곡선상의 모든 점의 (x, y) 좌표가되며, 매개 변수 t가 일정한 간격 [a, b], 일반적으로 [0, 1]에 걸쳐 변할 때 점을 얻습니다.
베 지어 곡선
프랑스 엔지니어가 베 지어 곡선을 발견했습니다. Pierre Bézier. 이러한 곡선은 다른 점의 제어하에 생성 될 수 있습니다. 제어점을 사용한 대략적인 접선은 곡선을 생성하는 데 사용됩니다. 베 지어 곡선은 수학적으로 다음과 같이 나타낼 수 있습니다.
$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$
어디 $p_{i}$ 점 집합이며 ${B_{i}^{n}}(t)$ 다음과 같이 주어진 번스타인 다항식을 나타냅니다.
$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$
어디 n 다항식 차수, i 인덱스이고 t 변수입니다.
가장 단순한 베 지어 곡선은 점으로부터의 직선입니다. $P_{0}$ ...에 $P_{1}$. 2 차 베 지어 곡선은 세 개의 제어점으로 결정됩니다. 큐빅 베 지어 곡선은 4 개의 제어점으로 결정됩니다.
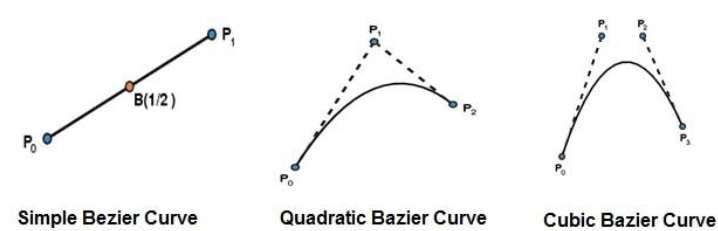
베 지어 곡선의 속성
베 지어 곡선에는 다음과 같은 속성이 있습니다.
일반적으로 제어점을 연결하는 세그먼트로 구성된 제어 다각형의 모양을 따릅니다.
그들은 항상 첫 번째와 마지막 제어점을 통과합니다.
그들은 정의하는 제어점의 볼록 껍질에 포함되어 있습니다.
곡선 세그먼트를 정의하는 다항식의 정도는 정의 다각형 점의 수보다 하나 적습니다. 따라서 4 개의 제어점에 대해 다항식의 차수는 3, 즉 3 차 다항식입니다.
베 지어 곡선은 일반적으로 정의하는 다각형의 모양을 따릅니다.
끝점에서 접선 벡터의 방향은 첫 번째 및 마지막 세그먼트로 결정된 벡터의 방향과 동일합니다.
베 지어 곡선의 볼록 껍질 속성은 다항식이 제어점을 부드럽게 따르도록합니다.
제어 다각형을 교차하는 것보다 더 많은 직선이 베 지어 곡선과 교차하지 않습니다.
아핀 변환에서는 변하지 않습니다.
베 지어 곡선은 전체적인 제어를 나타냅니다. 제어점을 이동하면 전체 곡선의 모양이 변경됩니다.
주어진 베 지어 곡선은 t = t0 지점에서 매개 변수 값 t = t0에 해당하는 지점에서 함께 연결되는 두 개의 베 지어 세그먼트로 세분화 될 수 있습니다.
B- 스플라인 곡선
번스타인 기저 함수에 의해 생성 된 베 지어 곡선은 유연성이 제한적입니다.
첫째, 지정된 다각형 정점의 수는 곡선을 정의하는 결과 다항식의 순서를 수정합니다.
두 번째 제한 특성은 혼합 함수의 값이 전체 곡선의 모든 매개 변수 값에 대해 0이 아니라는 것입니다.
B- 스플라인 기저에는 특별한 경우로 Bernstein 기저가 포함됩니다. B- 스플라인 기준은 비전 역입니다.
B- 스플라인 곡선은 제어점 Pi 및 B- 스플라인 기저 함수의 선형 조합으로 정의됩니다. $N_{i,}$ k (t)에 의해 주어진
$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$
어디,
{$p_{i}$: i = 0, 1, 2… .n}은 제어점입니다.
k는 B- 스플라인 곡선의 다항식 세그먼트 순서입니다. 차수 k는 곡선이 k-1 차의 조각 별 다항식 세그먼트로 구성됨을 의미합니다.
그만큼 $N_{i,k}(t)$"정규화 된 B- 스플라인 블렌딩 함수"입니다. 그것들은 순서 k와 일반적으로 "매듭 시퀀스"라고하는 실수의 비 감소 시퀀스로 설명됩니다.
$${t_{i}:i = 0, ... n + K}$$
N i , k 함수는 다음과 같이 설명됩니다.
$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$
k> 1이면
$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$
과
$$t \: \epsilon \: [t_{k-1},t_{n+1})$$
B- 스플라인 곡선의 속성
B- 스플라인 곡선에는 다음과 같은 속성이 있습니다.
모든 매개 변수 값에 대한 B- 스플라인 기저 함수의 합은 1입니다.
각 기저 함수는 모든 매개 변수 값에 대해 양수 또는 0입니다.
각 기본 함수에는 k = 1을 제외하고 정확히 하나의 최대 값이 있습니다.
곡선의 최대 순서는 다각형을 정의하는 정점 수와 같습니다.
B- 스플라인 다항식의 정도는 다각형을 정의하는 정점 수에 독립적입니다.
B- 스플라인을 사용하면 각 정점이 연관된 기저 함수가 0이 아닌 매개 변수 값 범위에 대해서만 곡선 모양에 영향을 미치기 때문에 곡선 표면에 대한 로컬 제어가 가능합니다.
곡선은 변동 감소 속성을 나타냅니다.
곡선은 일반적으로 다각형을 정의하는 모양을 따릅니다.
다각형을 정의하는 정점에 적용하여 모든 아핀 변환을 곡선에 적용 할 수 있습니다.
정의 다각형의 볼록 껍질 내의 곡선 선입니다.
다각형 표면
개체는 표면 모음으로 표시됩니다. 3D 객체 표현은 두 가지 범주로 나뉩니다.
Boundary Representations (B-reps) − 3D 개체를 환경과 개체 내부를 분리하는 표면 세트로 설명합니다.
Space–partitioning representations − 객체를 포함하는 공간 영역을 작고 겹치지 않는 연속적인 솔리드 세트 (일반적으로 큐브)로 분할하여 내부 속성을 설명하는 데 사용됩니다.
3D 그래픽 객체에 가장 일반적으로 사용되는 경계 표현은 객체 내부를 둘러싸는 표면 다각형 세트입니다. 많은 그래픽 시스템에서이 방법을 사용합니다. 객체 설명을 위해 다각형 세트가 저장됩니다. 이렇게하면 모든 표면을 선형 방정식으로 설명 할 수 있으므로 표면 렌더링 및 객체 표시가 단순화되고 속도가 빨라집니다.
다각형 표면은 설계 및 솔리드 모델링 응용 프로그램에서 일반적입니다. wireframe display표면 구조의 일반적인 표시를 제공하기 위해 신속하게 수행 할 수 있습니다. 그런 다음 다각형 표면에 음영 패턴을 보간하여 조명하여 사실적인 장면을 만듭니다.
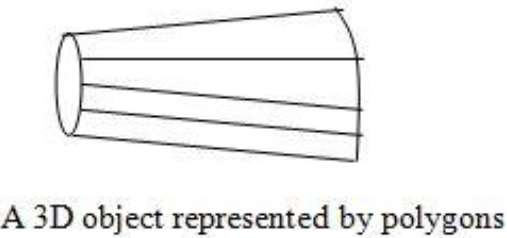
다각형 테이블
이 방법에서 표면은 정점 좌표 및 연관된 속성 세트로 지정됩니다. 다음 그림과 같이 v 1 에서 v 5 까지 5 개의 정점이 있습니다 .
각 꼭지점은 테이블에 v 1 : x 1 , y 1 , z 1 로 표시되는 x, y, z 좌표 정보를 저장합니다 .
Edge 테이블은 다각형의 모서리 정보를 저장하는 데 사용됩니다. 다음 그림에서 모서리 E 1 은 꼭지점 v 1 과 v 2 사이 에 있으며 표에서 E 1 : v 1 , v 2로 표시 됩니다.
다각형 표면 테이블은 다각형에있는 표면 수를 저장합니다. 다음 그림에서 표면 S 1 은 다각형 표면 테이블에서 S 1 : E 1 , E 2 및 E 3 로 표시 될 수있는 모서리 E 1 , E 2 및 E 3 로 덮여 있습니다 .
평면 방정식
평면 표면의 방정식은 다음과 같이 표현할 수 있습니다.
Ax + By + Cz + D = 0
여기서 (x, y, z)는 평면의 임의의 지점이고 계수 A, B, C 및 D는 평면의 공간 속성을 설명하는 상수입니다. 평면에서 동일 선상이 아닌 3 개의 점에 대한 좌표 값을 사용하여 3 개의 평면 방정식 세트를 풀면 A, B, C 및 D의 값을 얻을 수 있습니다. 평면의 세 꼭지점이 (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) 및 (x 3 , y 3 , z 3 ) 이라고 가정 해 보겠습니다 .
비율 A / D, B / D 및 C / D에 대해 다음 연립 방정식을 풀어 봅시다. A, B, C 및 D의 값을 얻습니다.
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
위의 식을 행렬식으로 구하려면 Cramer의 법칙을 위의 식에 적용하십시오.
$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$
매개 변수 A, B, C 및 D가있는 모든 점 (x, y, z)에 대해 다음과 같이 말할 수 있습니다.
Ax + By + Cz + D ≠ 0은 점이 평면에 없음을 의미합니다.
Ax + By + Cz + D <0은 점이 표면 내부에 있음을 의미합니다.
Ax + By + Cz + D> 0은 점이 표면 밖에 있음을 의미합니다.
다각형 메쉬
3D 표면 및 솔리드는 다각형 및 선 요소 세트로 근사화 할 수 있습니다. 이러한 표면을polygonal meshes. 다각형 메쉬에서 각 가장자리는 최대 두 개의 다각형이 공유합니다. 다각형 또는면 세트는 함께 개체의 "스킨"을 형성합니다.
이 방법은 그래픽에서 광범위한 솔리드 / 표면을 표현하는 데 사용할 수 있습니다. 숨겨진 표면 제거 알고리즘을 사용하여 다각형 메쉬를 렌더링 할 수 있습니다. 다각형 메쉬는 세 가지 방법으로 표현할 수 있습니다.
- 명시 적 표현
- 정점 목록에 대한 포인터
- 가장자리 목록에 대한 포인터
장점
- 거의 모든 객체를 모델링하는 데 사용할 수 있습니다.
- 정점 모음으로 표현하기 쉽습니다.
- 변형하기 쉽습니다.
- 컴퓨터 화면에 쉽게 그릴 수 있습니다.
단점
- 곡선 표면은 대략적으로 만 설명 할 수 있습니다.
- 머리카락이나 액체와 같은 일부 유형의 물체를 시뮬레이션하는 것은 어렵습니다.
불투명 한 물체와 표면이 포함 된 그림을 볼 때, 눈에 더 가까운 물체에서 뒤에있는 물체는 시야에서 볼 수 없습니다. 사실적인 화면 이미지를 얻으려면 이러한 숨겨진 표면을 제거해야합니다. 이러한 표면의 식별 및 제거를Hidden-surface problem.
숨겨진 표면 문제를 제거하는 두 가지 방법이 있습니다. Object-Space method 과 Image-space method. 객체 공간 방식은 물리적 좌표계로 구현되고 이미지 공간 방식은 화면 좌표계로 구현됩니다.
2D 화면에 3D 개체를 표시하려면 선택한보기 위치에서 보이는 화면 부분을 식별해야합니다.
깊이 버퍼 (Z 버퍼) 방법
이 방법은 Cutmull에 의해 개발되었습니다. 이미지 공간 접근 방식입니다. 기본 아이디어는 각 표면의 Z 깊이를 테스트하여 가장 가까운 (보이는) 표면을 결정하는 것입니다.
이 방법에서 각 표면은 표면을 가로 질러 한 번에 하나의 픽셀 위치를 개별적으로 처리합니다. 픽셀의 깊이 값이 비교되고 가장 가까운 (가장 작은 z) 표면이 프레임 버퍼에 표시 할 색상을 결정합니다.
폴리곤 표면에 매우 효율적으로 적용됩니다. 표면은 임의의 순서로 처리 할 수 있습니다. 먼 다각형에서 가까운 다각형을 재정의하려면frame buffer 과 depth buffer, 사용됩니다.
Depth buffer 표면이 처리 될 때 (x, y) 위치에 대한 깊이 값을 저장하는 데 사용됩니다 (0 ≤ 깊이 ≤ 1).
그만큼 frame buffer 각 위치 (x, y)에서 색상 값의 강도 값을 저장하는 데 사용됩니다.
z 좌표는 일반적으로 [0, 1] 범위로 정규화됩니다. z 좌표의 0 값은 후면 클리핑 창을 나타내고 z 좌표의 1 값은 전면 클리핑 창을 나타냅니다.
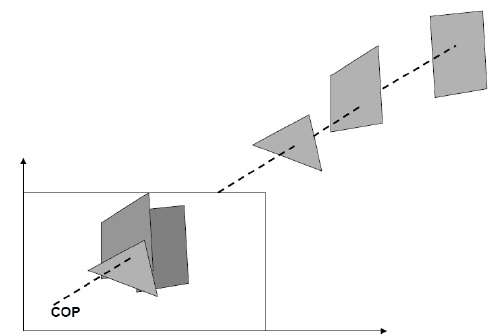
연산
Step-1 − 버퍼 값 설정 −
깊이 버퍼 (x, y) = 0
프레임 버퍼 (x, y) = 배경색
Step-2 − 각 폴리곤 처리 (한 번에 하나씩)
다각형의 투영 된 각 (x, y) 픽셀 위치에 대해 깊이 z를 계산합니다.
Z> 깊이 버퍼 (x, y) 인 경우
표면 색상 계산,
깊이 버퍼 설정 (x, y) = z,
프레임 버퍼 (x, y) = 표면 색상 (x, y)
장점
- 구현하기 쉽습니다.
- 하드웨어에 구현하면 속도 문제가 줄어 듭니다.
- 한 번에 하나의 개체를 처리합니다.
단점
- 대용량 메모리가 필요합니다.
- 시간이 많이 걸리는 과정입니다.
스캔 라인 방식
보이는 표면을 식별하는 이미지 공간 방법입니다. 이 방법에는 단일 스캔 라인에 대한 깊이 정보 만 있습니다. 깊이 값의 하나의 스캔 라인을 요구하려면 다음 스캔 라인을 처리하기 전에 주어진 스캔 라인을 교차하는 모든 다각형을 동시에 그룹화하고 처리해야합니다. 두 개의 중요한 테이블,edge table 과 polygon table, 이를 위해 유지됩니다.
The Edge Table − 장면에있는 각 선의 좌표 끝점, 각 선의 역 기울기, 모서리를 표면에 연결하는 다각형 테이블에 대한 포인터가 포함됩니다.
The Polygon Table − 여기에는 평면 계수, 표면 재료 속성, 기타 표면 데이터가 포함되며 모서리 테이블에 대한 포인터가 될 수 있습니다.

주어진 스캔 라인을 가로 지르는 표면 검색을 용이하게하기 위해 활성 모서리 목록이 형성됩니다. 활성 목록은 x가 증가하는 순서로 스캔 라인을 교차하는 모서리 만 저장합니다. 또한 각 표면에 대한 플래그가 설정되어 스캔 선을 따라 위치가 표면 내부 또는 외부에 있는지 여부를 나타냅니다.
각 스캔 라인의 픽셀 위치는 왼쪽에서 오른쪽으로 처리됩니다. 표면과 왼쪽 교차점에서 표면 플래그가 켜지고 오른쪽에서 플래그가 꺼집니다. 여러 표면이 특정 스캔 라인 위치에서 플래그를 켠 경우에만 깊이 계산을 수행하면됩니다.
영역 분할 방법
면적 세분화 방법은 단일 표면의 일부를 나타내는 뷰 영역을 찾아서 활용합니다. 각 작은 영역이 하나의 보이는 표면의 일부가 투영되거나 전혀 표면이 없을 때까지 전체보기 영역을 더 작고 작은 직사각형으로 나눕니다.
세분화가 단일 표면에 속하는 것으로 쉽게 분석되거나 단일 픽셀 크기로 축소 될 때까지이 프로세스를 계속합니다. 이를 수행하는 쉬운 방법은 각 단계에서 영역을 4 개의 동일한 부분으로 연속적으로 나누는 것입니다. 지정된 영역 경계와 표면이 가질 수있는 네 가지 가능한 관계가 있습니다.
Surrounding surface − 영역을 완전히 둘러싸는 것.
Overlapping surface − 부분적으로 영역 내부와 부분 외부에있는 것.
Inside surface − 완전히 영역 안에있는 것.
Outside surface − 완전히 영역 밖에있는 것.
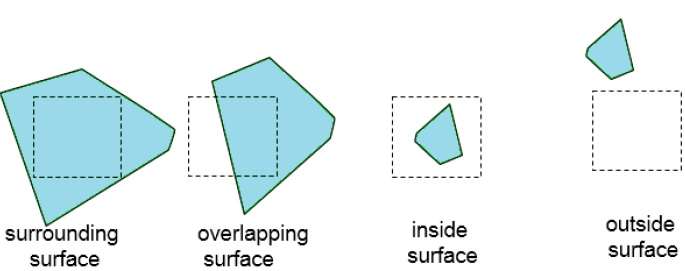
영역 내 표면 가시성을 결정하기위한 테스트는이 네 가지 분류 측면에서 설명 할 수 있습니다. 다음 조건 중 하나가 참이면 지정된 영역의 추가 세분화가 필요하지 않습니다.
- 모든 표면은 영역에 대한 외부 표면입니다.
- 내부, 겹치거나 주변 표면이 영역에 하나만 있습니다.
- 주변 표면은 면적 경계 내의 다른 모든 표면을가립니다.
뒷면 감지
다면체의 뒷면을 식별하기위한 빠르고 간단한 객체 공간 방법은 "내부-외부"테스트를 기반으로합니다. 점 (x, y, z)은 평면 매개 변수 A, B, C 및 D가있는 다각형 표면의 "내부"입니다. 내부 점이 표면에 대한 시선을 따라있을 때 다각형은 뒷면 ( 우리는 그 얼굴 안에 있고 우리가 보는 위치에서 앞을 볼 수 없습니다).
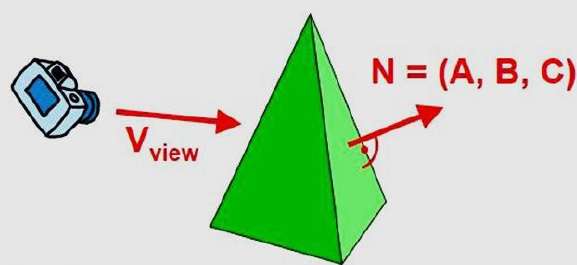
정규 벡터를 고려하여이 테스트를 단순화 할 수 있습니다. N 데카르트 구성 요소 (A, B, C)가있는 다각형 표면에.
일반적으로 V가 눈 (또는 "카메라") 위치에서 보는 방향의 벡터 인 경우이 다각형은 다음과 같은 경우 뒷면입니다.
V.N > 0
또한 객체 설명이 투영 좌표로 변환되고보기 방향이보기 z 축과 평행하면-
V = (0, 0, V z ) 및 V.N = V Z C
그래서 우리는 정규 벡터의 구성 요소 인 C의 부호 만 고려하면됩니다. N.
네거티브를 따라 보는 방향이있는 오른 손잡이보기 시스템에서 $Z_{V}$축, 다각형은 C <0이면 뒷면입니다. 또한보기 방향이 해당 다각형을 향하기 때문에 법선에 z 구성 요소 C = 0 인면을 볼 수 없습니다. 따라서 일반적으로 법선 벡터에 z 성분 값이 있으면 모든 다각형에 뒷면으로 레이블을 지정할 수 있습니다.
C <= 0
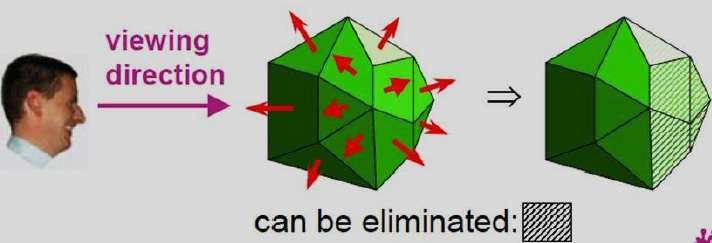
왼손잡이보기 시스템을 사용하는 패키지에서도 유사한 방법을 사용할 수 있습니다. 이 패키지에서 평면 매개 변수 A, B, C 및 D는 시계 방향으로 지정된 다각형 정점 좌표에서 계산할 수 있습니다 (오른쪽 시스템에서 사용되는 시계 반대 방향과는 다름).
또한 뒷면에는보기 위치에서 멀어지는 법선 벡터가 있으며보기 방향이 양수를 따를 때 C> = 0으로 식별됩니다. $Z_{v}$중심선. 객체를 정의하는 여러 평면에 대한 매개 변수 C를 검사하여 모든 뒷면을 즉시 식별 할 수 있습니다.
A 버퍼 방법
A 버퍼 방법은 깊이 버퍼 방법의 확장입니다. A- 버퍼 방법은 루카스 필름 스튜디오에서 렌더링 시스템을 위해 개발 한 가시성 감지 방법입니다.
A 버퍼는 깊이 버퍼 방법에서 확장되어 투명도를 허용합니다. A 버퍼의 주요 데이터 구조는 누적 버퍼입니다.
A 버퍼의 각 위치에는 두 개의 필드가 있습니다.
Depth field − 양수 또는 음수 실수를 저장합니다.
Intensity field − 표면 강도 정보 또는 포인터 값을 저장합니다.

깊이가 0보다 크면 해당 위치에 저장된 숫자는 해당 픽셀 영역과 겹치는 단일 표면의 깊이입니다. 그런 다음 강도 필드는 해당 지점에서 표면 색상의 RGB 구성 요소와 픽셀 적용 비율을 저장합니다.
깊이 <0이면 픽셀 강도에 대한 다중 표면 기여를 나타냅니다. 그런 다음 강도 필드는 표면 데이터의 링크 된 목록에 대한 포인터를 저장합니다. A 버퍼의 표면 버퍼에는 다음이 포함됩니다.
- RGB 강도 구성 요소
- 불투명도 매개 변수
- Depth
- 면적 비율
- 표면 식별자
알고리즘은 깊이 버퍼 알고리즘처럼 진행됩니다. 깊이 및 불투명도 값은 픽셀의 최종 색상을 결정하는 데 사용됩니다.
깊이 분류 방법
깊이 정렬 방법은 이미지 공간과 객체 공간 작업을 모두 사용합니다. 깊이 정렬 방법은 두 가지 기본 기능을 수행합니다.
첫째, 표면은 깊이가 감소하는 순서로 정렬됩니다.
둘째, 표면은 깊이가 가장 큰 표면부터 순서대로 스캔 변환됩니다.
다각형 표면의 스캔 변환은 이미지 공간에서 수행됩니다. 숨겨진 표면 문제를 해결하기위한이 방법은 종종painter's algorithm. 다음 그림은 깊이 정렬의 효과를 보여줍니다.
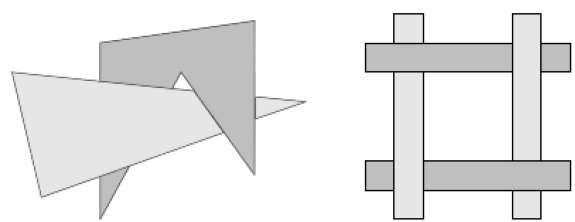
알고리즘은 깊이별로 정렬하여 시작합니다. 예를 들어, 폴리곤의 초기 "깊이"추정치는 폴리곤의 모든 정점에서 가장 가까운 z 값으로 간주 될 수 있습니다.
목록 끝에있는 다각형 P를 가져 오겠습니다. z 범위가 P와 겹치는 모든 다각형 Q를 고려하십시오. P를 그리기 전에 다음 테스트를 수행합니다. 다음 테스트 중 하나라도 양성이면 Q보다 먼저 P를 그릴 수 있다고 가정 할 수 있습니다.
- x 범위가 겹치지 않습니까?
- y 범위가 겹치지 않습니까?
- P는 관점에서 완전히 Q 평면의 반대편에 있습니까?
- Q는 완전히 관점과 P 평면의 같은면에 있습니까?
- 다각형의 투영이 겹치지 않습니까?
모든 테스트가 실패하면 다른 평면을 사용하여 P 또는 Q를 분할합니다. 새로운 절단 다각형이 깊이 순서에 삽입되고 프로세스가 계속됩니다. 이론적으로이 분할은 O (n 2 ) 개의 개별 다각형을 생성 할 수 있지만 실제로는 다각형의 수가 훨씬 적습니다.
이진 공간 파티션 (BSP) 트리
이진 공간 분할은 가시성을 계산하는 데 사용됩니다. BSP 나무를 만들려면 다각형으로 시작하고 모든 가장자리에 레이블을 지정해야합니다. 한 번에 하나의 가장자리 만 처리하고 각 가장자리를 확장하여 평면을 둘로 분할합니다. 트리의 첫 번째 가장자리를 루트로 배치합니다. 내부 또는 외부에 따라 후속 모서리를 추가합니다. 이미 트리에있는 가장자리의 확장에 걸쳐있는 가장자리는 두 개로 분할되고 둘 다 트리에 추가됩니다.

위 그림에서 먼저 A 뿌리로.
그림 (a)의 모든 노드 목록을 작성하십시오.
루트 앞에있는 모든 노드를 넣으십시오. A 노드의 왼쪽에 A 루트 뒤에있는 모든 노드를 A 그림 (b)와 같이 오른쪽으로.
모든 전면 노드를 먼저 처리 한 다음 뒤에있는 노드를 처리합니다.
그림 (c)와 같이 먼저 노드를 처리합니다. B. 노드 앞에 아무것도 없기 때문에B, 우리는 NIL을 넣었습니다. 그러나 우리는 노드가C 노드 뒤 B, 그래서 노드 C 노드의 오른쪽으로 이동합니다. B.
노드에 대해 동일한 프로세스를 반복하십시오. D.
프랑스 / 미국의 수학자 Benoit Mandelbrot 박사가 프랙탈을 발견했습니다. 프랙탈이라는 단어는 부서짐 을 의미 하는 라틴어 프랙 터스 에서 파생되었습니다 .
프랙탈은 무엇입니까?
프랙탈은 컴퓨터가 단일 공식으로 생성 한 매우 복잡한 그림입니다. 반복을 사용하여 생성됩니다. 이는 이전 반복의 결과를 고려하여 하나의 수식이 약간 다른 값으로 반복해서 반복됨을 의미합니다.
프랙탈은 다음과 같은 많은 영역에서 사용됩니다.
Astronomy − 은하, 토성의 고리 등을 분석합니다.
Biology/Chemistry − 박테리아 배양, 화학 반응, 인체 해부학, 분자, 식물,
Others − 구름, 해안선 및 경계선, 데이터 압축, 확산, 경제, 프랙탈 아트, 프랙탈 음악, 풍경, 특수 효과 등을 묘사합니다.

프랙탈 생성
다음 그림과 같이 동일한 모양을 반복해서 반복하여 프랙탈을 생성 할 수 있습니다. 그림 (a)는 정삼각형을 보여줍니다. 그림 (b)에서 삼각형이 반복되어 별 모양을 만드는 것을 볼 수 있습니다. 그림 (c)에서 그림 (b)의 별 모양이 반복해서 반복되어 새로운 모양이 만들어지는 것을 볼 수 있습니다.
원하는 모양을 만들기 위해 무제한 반복을 수행 할 수 있습니다. 프로그래밍 측면에서 재귀는 이러한 모양을 만드는 데 사용됩니다.

기하학적 프랙탈
기하학적 프랙탈은 정수 또는 프랙탈 차원이 아닌 자연에서 발견되는 모양을 다룹니다. 결정 론적 (비 랜덤) 자기 유사 프랙탈을 기하학적으로 구성하기 위해, 우리는initiator. 이니시에이터의 하위 부분은 다음 패턴으로 대체됩니다.generator.

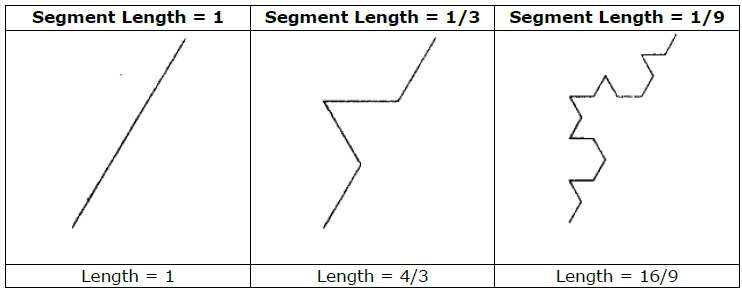
예를 들어 위의 그림과 같은 Initiator와 Generator를 사용하면 반복하여 좋은 패턴을 구성 할 수 있습니다. 이니시에이터의 각 직선 세그먼트는 각 단계에서 동일한 길이의 선 세그먼트 4 개로 대체됩니다. 배율 인수는 1/3이므로 프랙탈 차원은 D = ln 4 / ln 3 ≈ 1.2619입니다.
또한 이니시에이터의 각 선분의 길이는 각 단계에서 4/3 씩 증가하므로 다음 그림과 같이 곡선에 더 많은 세부 사항이 추가됨에 따라 프랙탈 곡선의 길이가 무한대가되는 경향이 있습니다.
애니메이션은 컴퓨터 그래픽의 모든 개체에 생명을 불어 넣는 것을 의미합니다. 그것은 가장 무생물처럼 보이는 물체에 에너지와 감정을 주입하는 힘을 가지고 있습니다. 컴퓨터 지원 애니메이션과 컴퓨터 생성 애니메이션은 컴퓨터 애니메이션의 두 가지 범주입니다. 영화 나 비디오를 통해 발표 할 수 있습니다.
애니메이션의 기본 아이디어는 녹화 된 이미지를 사람의 눈을 속여 연속적인 동작으로 해석 할 수있을만큼 빠른 속도로 재생하는 것입니다. 애니메이션은 일련의 죽은 이미지를 생생하게 만들 수 있습니다. 애니메이션은 엔터테인먼트, 컴퓨터 지원 설계, 과학 시각화, 교육, 교육, 전자 상거래 및 컴퓨터 아트와 같은 많은 영역에서 사용할 수 있습니다.
애니메이션 기법
애니메이터는 다양한 애니메이션 기술을 발명하고 사용했습니다. 기본적으로이 섹션에서 하나씩 논의 할 6 가지 애니메이션 기술이 있습니다.
전통 애니메이션 (프레임 별)
전통적으로 대부분의 애니메이션은 수작업으로 이루어졌습니다. 애니메이션의 모든 프레임은 손으로 그려야했습니다. 애니메이션의 1 초당 24 프레임 (필름)이 필요하기 때문에 가장 짧은 영화를 만드는 데 필요한 노력은 엄청날 수 있습니다.
키 프레임
이 기법에서는 스토리 보드를 배치 한 다음 아티스트가 애니메이션의 주요 프레임을 그립니다. 주요 프레임은 눈에 띄는 변화가 발생하는 프레임입니다. 애니메이션의 핵심 포인트입니다. 키 프레이밍을 사용하려면 애니메이터가 객체의 중요 또는 주요 위치를 지정해야합니다. 그런 다음 컴퓨터는 해당 위치 사이를 부드럽게 보간하여 누락 된 프레임을 자동으로 채 웁니다.
절차 적
절차 적 애니메이션에서 객체는 키 프레임이 아닌 절차 (규칙 집합)에 의해 애니메이션됩니다. 애니메이터는 규칙과 초기 조건을 지정하고 시뮬레이션을 실행합니다. 규칙은 종종 수학 방정식으로 표현 된 실제 세계의 물리적 규칙을 기반으로합니다.
행동
행동 애니메이션에서 자율적 캐릭터는 적어도 어느 정도는 자신의 행동을 결정합니다. 이를 통해 캐릭터는 즉석에서 작업 할 수 있으며 애니메이터는 모든 캐릭터 모션의 각 세부 사항을 지정할 필요가 없습니다.
성능 기반 (모션 캡처)
또 다른 기술은 자기 또는 시각 기반 센서가 사람이나 동물 물체의 동작을 3 차원으로 기록하는 모션 캡처입니다. 그런 다음 컴퓨터는 이러한 데이터를 사용하여 개체를 애니메이션합니다.
이 기술은 많은 유명 운동 선수들이 스포츠 비디오 게임의 캐릭터에게 액션을 제공 할 수있게했습니다. 모션 캡처는 주로 일반적인 인간 동작 중 일부를 상대적으로 쉽게 캡처 할 수 있기 때문에 애니메이터에게 매우 인기가 있습니다. 그러나 피사체와 그래픽 캐릭터의 모양이나 치수간에 심각한 차이가있을 수 있으며 이로 인해 정확한 실행에 문제가 발생할 수 있습니다.
물리적 기반 (동적)
키 프레이밍 및 영화와 달리 시뮬레이션은 물리 법칙을 사용하여 사진 및 기타 물체의 움직임을 생성합니다. 시뮬레이션은 물리적 사실성을 유지하면서 약간 다른 시퀀스를 생성하는 데 쉽게 사용할 수 있습니다. 둘째, 실시간 시뮬레이션은 실제 사람이 시뮬레이션 된 캐릭터의 동작을 조작 할 수있는 더 높은 수준의 상호 작용을 허용합니다.
반대로 키 프레임 및 모션 선택 및 수정을 기반으로하는 애플리케이션은 미리 계산 된 모션 라이브러리를 형성합니다. 시뮬레이션이 겪는 한 가지 단점은 적절한 제어 시스템을 제작하는 데 필요한 전문 지식과 시간입니다.
키 프레이밍
키 프레임은 애니메이션의 변경 사항을 정의하는 프레임입니다. 프레임 별 애니메이션을 만들 때 모든 프레임은 키 프레임입니다. 누군가 컴퓨터에서 3D 애니메이션을 만들 때 일반적으로 모든 단일 프레임에서 주어진 개체의 정확한 위치를 지정하지 않습니다. 키 프레임을 만듭니다.
키 프레임은 개체가 크기, 방향, 모양 또는 기타 속성을 변경하는 동안 중요한 프레임입니다. 그런 다음 컴퓨터는 모든 중간 프레임을 파악하여 애니메이터의 시간을 대폭 절약합니다. 다음 그림은 사용자가 그린 프레임과 컴퓨터가 생성 한 프레임을 나타냅니다.


모핑
한 형태에서 다른 형태로의 개체 형태 변형을 모핑이라고합니다. 가장 복잡한 변형 중 하나입니다.

모프는 마치 두 이미지가 매우 유동적 인 움직임으로 서로 녹아 드는 것처럼 보입니다. 기술적 인 측면에서 두 개의 이미지가 왜곡되고 그 사이에 페이드가 발생합니다.