원 생성 알고리즘
화면에 원을 그리는 것은 선을 그리는 것보다 조금 복잡합니다. 원을 생성하는 두 가지 인기있는 알고리즘이 있습니다.Bresenham’s Algorithm 과 Midpoint Circle Algorithm. 이러한 알고리즘은 원을 그리는 데 필요한 후속 점을 결정한다는 아이디어를 기반으로합니다. 알고리즘에 대해 자세히 논의 해 보겠습니다.
원의 방정식은 $ X ^ {2} + Y ^ {2} = r ^ {2}, $이며 여기서 r은 반지름입니다.
Bresenham의 알고리즘
래스터 표시에 연속 호를 표시 할 수 없습니다. 대신 가장 가까운 픽셀 위치를 선택하여 호를 완성해야합니다.
다음 그림에서 픽셀을 (X, Y) 위치에 배치했으며 이제 N (X + 1, Y) 또는 S (X + 1)에 다음 픽셀을 배치 할 위치를 결정해야합니다. Y-1).
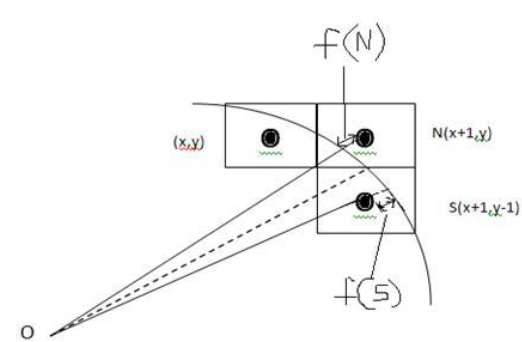
이는 결정 매개 변수에 의해 결정될 수 있습니다. d.
- d <= 0이면 N (X + 1, Y)이 다음 픽셀로 선택됩니다.
- d> 0이면 S (X + 1, Y-1)가 다음 픽셀로 선택됩니다.
연산
Step 1− 원과 반경의 중심 좌표를 구하여 각각 x, y, R에 저장합니다. P = 0 및 Q = R을 설정합니다.
Step 2 − 결정 매개 변수 D = 3 – 2R을 설정합니다.
Step 3 − P ≤ Q 동안 8 단계를 반복합니다.
Step 4 − 원 그리기 (X, Y, P, Q)를 호출합니다.
Step 5 − P 값을 증가시킵니다.
Step 6 − D <0이면 D = D + 4P + 6.
Step 7 − 그렇지 않으면 R = R-1, D = D + 4 (PQ) + 10을 설정합니다.
Step 8 − 원 그리기 (X, Y, P, Q)를 호출합니다.
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).중간 점 알고리즘
Step 1 − 입력 반경 r 원 중심 $ (x_ {c,} y_ {c}) $ 원점을 중심으로하는 원의 원주에 대한 첫 번째 점을 다음과 같이 구합니다.
(x0, y0) = (0, r)Step 2 − 결정 매개 변수의 초기 값을 다음과 같이 계산합니다.
$ P_ {0} $ = 5/4 – r (이 등식을 단순화하려면 다음 설명을 참조하십시오.)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0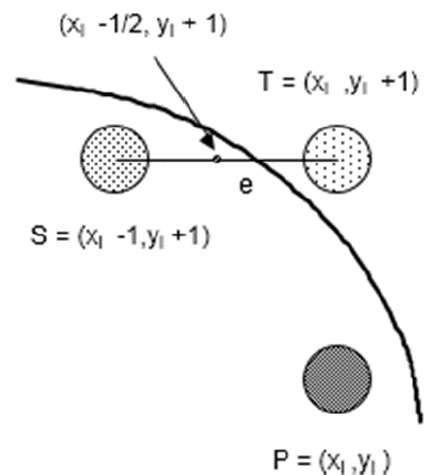
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 − K = 0에서 시작하는 각 $ X_ {K} $ 위치에서 다음 테스트를 수행합니다. −
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
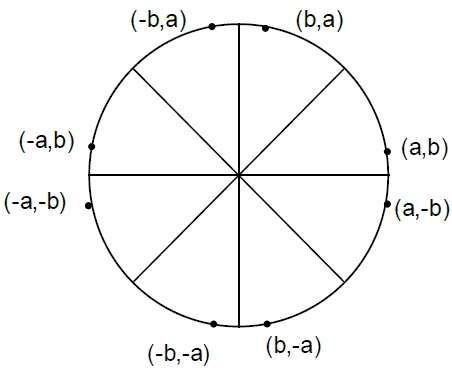
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 − 다른 7 개의 8 분원에서 대칭점을 결정합니다.
Step 5 − 각 계산 픽셀 위치 (X, Y)를 $ (X_ {C,} Y_ {C}) $ 중심의 원형 경로로 이동하고 좌표 값을 플로팅합니다.
X = X + XC, Y = Y + YCStep 6 − X> = Y가 될 때까지 3-5 단계를 반복합니다.