컴퓨터 그래픽 표면
다각형 표면
개체는 표면 모음으로 표시됩니다. 3D 객체 표현은 두 가지 범주로 나뉩니다.
Boundary Representations (B-reps) − 3D 개체를 환경과 개체 내부를 분리하는 표면 집합으로 설명합니다.
Space–partitioning representations − 객체를 포함하는 공간 영역을 작고 겹치지 않는 연속적인 솔리드 (일반적으로 큐브) 세트로 분할하여 내부 속성을 설명하는 데 사용됩니다.
3D 그래픽 객체에 가장 일반적으로 사용되는 경계 표현은 객체 내부를 둘러싸는 표면 다각형 세트입니다. 많은 그래픽 시스템에서이 방법을 사용합니다. 객체 설명을 위해 다각형 세트가 저장됩니다. 이렇게하면 모든 표면을 선형 방정식으로 설명 할 수 있으므로 표면 렌더링 및 객체 표시가 단순화되고 속도가 빨라집니다.
다각형 표면은 설계 및 솔리드 모델링 응용 프로그램에서 일반적입니다. wireframe display표면 구조의 일반적인 표시를 제공하기 위해 신속하게 수행 할 수 있습니다. 그런 다음 다각형 표면에 음영 패턴을 보간하여 조명하여 사실적인 장면을 만듭니다.
다각형 테이블
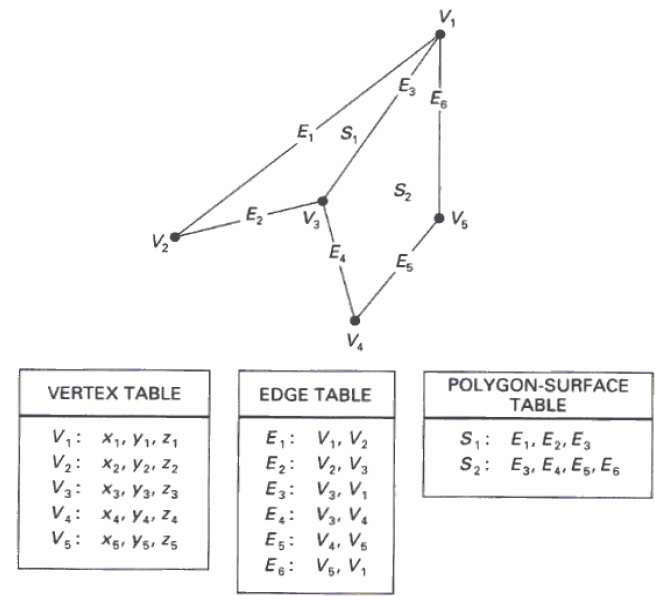
이 방법에서 표면은 정점 좌표 및 연관된 속성 세트로 지정됩니다. 다음 그림에 표시된대로 v 1 에서 v 5 까지 5 개의 정점이 있습니다 .
각 꼭지점은 테이블에 v 1 : x 1 , y 1 , z 1 로 표시되는 x, y, z 좌표 정보를 저장합니다 .
Edge 테이블은 다각형의 모서리 정보를 저장하는 데 사용됩니다. 다음 그림에서 모서리 E 1 은 꼭지점 v 1 과 v 2 사이 에 있으며 테이블에서 E 1 : v 1 , v 2로 표시 됩니다.
다각형 표면 테이블은 다각형에있는 표면 수를 저장합니다. 다음 그림에서 표면 S 1 은 모서리 E 1 , E 2 및 E 3 로 덮여 있으며 다각형 표면 테이블에서 S 1 : E 1 , E 2 , E 3로 표시 될 수 있습니다.
평면 방정식
평면 표면의 방정식은 다음과 같이 표현할 수 있습니다.
Ax + By + Cz + D = 0
여기서 (x, y, z)는 평면의 임의의 지점이고 계수 A, B, C 및 D는 평면의 공간 속성을 설명하는 상수입니다. 평면에서 동일 선상에 있지 않은 세 점의 좌표 값을 사용하여 세 개의 평면 방정식 세트를 풀면 A, B, C, D의 값을 얻을 수 있습니다. 평면의 세 꼭지점이 (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) 및 (x 3 , y 3 , z 3 ) 이라고 가정 해 보겠습니다 .
비율 A / D, B / D 및 C / D에 대해 다음 연립 방정식을 풀어 봅시다. A, B, C 및 D의 값을 얻습니다.
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
위의 식을 행렬식으로 구하려면 위 식에 Cramer의 법칙을 적용하십시오.
$ A = \ begin {bmatrix} 1 & y_ {1} & z_ {1} \\ 1 & y_ {2} & z_ {2} \\ 1 & y_ {3} & z_ {3} \ end {bmatrix} B = \ 시작 {bmatrix} x_ {1} & 1 & z_ {1} \\ x_ {2} & 1 & z_ {2} \\ x_ {3} & 1 & z_ {3} \ end {bmatrix} C = \ begin {bmatrix} x_ {1} & y_ {1} & 1 \\ x_ {2} & y_ {2} & 1 \\ x_ {3} & y_ {3} & 1 \ end {bmatrix} D =-\ begin {bmatrix} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \ end {bmatrix } $
매개 변수 A, B, C 및 D가있는 모든 점 (x, y, z)에 대해 다음과 같이 말할 수 있습니다.
Ax + By + Cz + D ≠ 0은 점이 평면에 없음을 의미합니다.
Ax + By + Cz + D <0은 점이 표면 내부에 있음을 의미합니다.
Ax + By + Cz + D> 0은 점이 표면 밖에 있음을 의미합니다.
다각형 메쉬
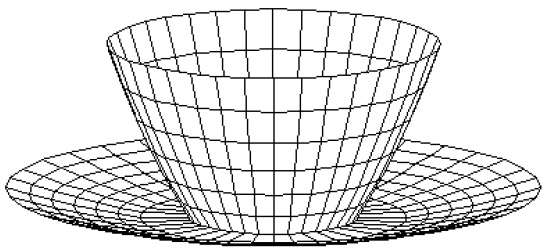
3D 표면 및 솔리드는 다각형 및 선 요소 세트로 근사화 할 수 있습니다. 이러한 표면을polygonal meshes. 다각형 메쉬에서 각 가장자리는 최대 두 개의 다각형이 공유합니다. 다각형 또는면 세트는 함께 개체의 "스킨"을 형성합니다.
이 방법은 그래픽에서 광범위한 솔리드 / 표면을 표현하는 데 사용할 수 있습니다. 숨겨진 표면 제거 알고리즘을 사용하여 다각형 메쉬를 렌더링 할 수 있습니다. 다각형 메쉬는 세 가지 방법으로 표현할 수 있습니다.
- 명시 적 표현
- 정점 목록에 대한 포인터
- 가장자리 목록에 대한 포인터
장점
- 거의 모든 객체를 모델링하는 데 사용할 수 있습니다.
- 정점 모음으로 표현하기 쉽습니다.
- 변형하기 쉽습니다.
- 컴퓨터 화면에 쉽게 그릴 수 있습니다.
단점
- 곡선 표면은 대략적으로 만 설명 할 수 있습니다.
- 머리카락이나 액체와 같은 일부 유형의 물체를 시뮬레이션하는 것은 어렵습니다.