컴퓨터 그래픽 곡선
컴퓨터 그래픽에서 우리는 종종 화면에 다양한 유형의 개체를 그려야합니다. 개체는 항상 평평하지 않으며 개체를 그리기 위해 곡선을 여러 번 그려야합니다.
곡선 유형
곡선은 무한히 큰 점 집합입니다. 각 점에는 끝점을 제외하고 두 개의 이웃이 있습니다. 곡선은 크게 세 가지 범주로 분류 할 수 있습니다.explicit, implicit, 과 parametric curves.
암시 적 곡선
암시 적 곡선 표현은 곡선에 점이 있는지 확인하기 위해 테스트 할 수있는 절차를 사용하여 곡선의 점 집합을 정의합니다. 일반적으로 암시 적 곡선은 다음 형식의 암시 적 함수로 정의됩니다.
f (x, y) = 0
다중 값 곡선 (x 값에 대해 여러 y 값)을 나타낼 수 있습니다. 일반적인 예는 암시 적 표현이 다음과 같은 원입니다.
x2 + y2 - R2 = 0
명시 적 곡선
수학 함수 y = f (x)를 곡선으로 그릴 수 있습니다. 이러한 함수는 곡선의 명시 적 표현입니다. 명시 적 표현은 수직선을 나타낼 수없고 단일 값이기 때문에 일반적이지 않습니다. x의 각 값에 대해 함수는 일반적으로 y의 단일 값만 계산합니다.
파라 메트릭 곡선
파라 메트릭 형태의 커브를 파라 메트릭 커브라고합니다. 명시 적 및 암시 적 곡선 표현은 함수가 알려진 경우에만 사용할 수 있습니다. 실제로는 파라 메트릭 곡선이 사용됩니다. 2 차원 파라 메트릭 곡선의 형태는 다음과 같습니다.
P (t) = f (t), g (t) 또는 P (t) = x (t), y (t)
함수 f와 g는 곡선상의 모든 점의 (x, y) 좌표가되며, 매개 변수 t가 일정한 간격 [a, b], 일반적으로 [0, 1]에 걸쳐 변경 될 때 점을 얻습니다.
베 지어 곡선
프랑스 엔지니어가 베 지어 곡선을 발견했습니다. Pierre Bézier. 이러한 곡선은 다른 점의 제어하에 생성 될 수 있습니다. 제어점을 사용한 대략적인 접선은 곡선을 생성하는 데 사용됩니다. 베 지어 곡선은 수학적으로 다음과 같이 나타낼 수 있습니다.
$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$
$ p_ {i} $는 점의 집합이고 $ {B_ {i} ^ {n}} (t) $는 다음과 같이 주어진 번스타인 다항식을 나타냅니다.
$$ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1-t) ^ {ni} t ^ {i} $$
어디 n 다항식 차수, i 인덱스이고 t 변수입니다.
가장 간단한 베 지어 곡선은 $ P_ {0} $ 지점에서 $ P_ {1} $까지의 직선입니다. 2 차 베 지어 곡선은 세 개의 제어점으로 결정됩니다. 큐빅 베 지어 곡선은 4 개의 제어점으로 결정됩니다.
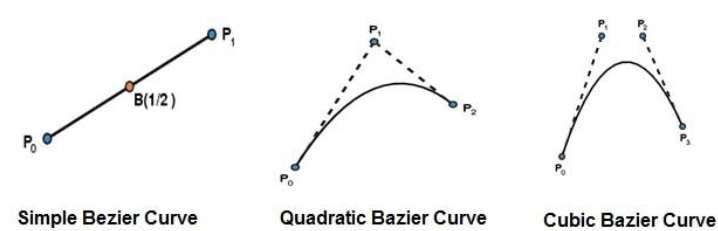
베 지어 곡선의 속성
베 지어 곡선에는 다음과 같은 속성이 있습니다.
일반적으로 제어점을 연결하는 세그먼트로 구성된 제어 다각형의 모양을 따릅니다.
그들은 항상 첫 번째와 마지막 제어점을 통과합니다.
그들은 정의하는 제어점의 볼록 껍질에 포함되어 있습니다.
곡선 세그먼트를 정의하는 다항식의 정도는 정의 다각형 점의 수보다 하나 적습니다. 따라서 4 개의 제어점에 대해 다항식의 차수는 3, 즉 3 차 다항식입니다.
베 지어 곡선은 일반적으로 정의하는 다각형의 모양을 따릅니다.
끝점에서 접선 벡터의 방향은 첫 번째 및 마지막 세그먼트로 결정된 벡터의 방향과 동일합니다.
베 지어 곡선의 볼록 껍질 속성은 다항식이 제어점을 부드럽게 따르도록합니다.
제어 다각형을 교차하는 것보다 베 지어 곡선을 더 많이 교차하는 직선은 없습니다.
아핀 변환에서는 변하지 않습니다.
베 지어 곡선은 전역 제어를 나타냅니다. 즉, 제어점을 이동하면 전체 곡선의 모양이 변경됩니다.
주어진 베 지어 곡선은 t = t0 지점에서 매개 변수 값 t = t0에 해당하는 지점에서 함께 연결되는 두 개의 베 지어 세그먼트로 세분화 될 수 있습니다.
B- 스플라인 곡선
번스타인 기저 함수에 의해 생성 된 베 지어 곡선은 유연성이 제한적입니다.
첫째, 지정된 다각형 정점의 수는 곡선을 정의하는 결과 다항식의 순서를 수정합니다.
두 번째 제한 특성은 혼합 함수의 값이 전체 곡선의 모든 매개 변수 값에 대해 0이 아니라는 것입니다.
B- 스플라인 기저에는 특별한 경우로 Bernstein 기저가 포함됩니다. B- 스플라인 기준은 비전 역입니다.
B- 스플라인 곡선은 제어점 Pi와 B- 스플라인 기저 함수 $ N_ {i,} $ k (t)의 선형 조합으로 정의됩니다.
$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \ : \ epsilon \ : [ tk-1, tn + 1] $
어디,
{$ p_ {i} $ : i = 0, 1, 2… .n}은 제어점입니다.
k는 B- 스플라인 곡선의 다항식 세그먼트 순서입니다. 차수 k는 곡선이 k-1 차의 조각 별 다항식 세그먼트로 구성됨을 의미합니다.
$ N_ {i, k} (t) $는 "정규화 된 B- 스플라인 블렌딩 함수"입니다. 그것들은 순서 k와 일반적으로“매듭 수열”이라고 불리는 감소하지 않는 실수 수열로 설명됩니다.
$$ {t_ {i} : i = 0, ... n + K} $$
N i , k 함수는 다음과 같이 설명됩니다.
$$ N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \ : u \ : \ epsilon \ : [t_ {i,} t_ {i + 1}) \\ 0 , & 그렇지 않으면 \ end {matrix} \ right. $$
k> 1이면
$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k}-t_ {i + 1}} N_ {i + 1, k-1} (t) $$
과
$$ t \ : \ 엡실론 \ : [t_ {k-1}, t_ {n + 1}) $$
B- 스플라인 곡선의 속성
B- 스플라인 곡선에는 다음과 같은 속성이 있습니다.
모든 매개 변수 값에 대한 B- 스플라인 기저 함수의 합은 1입니다.
각 기저 함수는 모든 매개 변수 값에 대해 양수 또는 0입니다.
각 기본 함수에는 k = 1을 제외하고 정확히 하나의 최대 값이 있습니다.
곡선의 최대 순서는 정의 다각형의 정점 수와 같습니다.
B- 스플라인 다항식의 정도는 다각형을 정의하는 정점 수에 독립적입니다.
B- 스플라인을 사용하면 각 정점이 연관된 기저 함수가 0이 아닌 매개 변수 값 범위에 대해서만 곡선 모양에 영향을주기 때문에 곡선 표면에 대한 로컬 제어가 가능합니다.
곡선은 변동 감소 속성을 나타냅니다.
곡선은 일반적으로 다각형을 정의하는 모양을 따릅니다.
다각형을 정의하는 정점에 적용하여 모든 아핀 변환을 곡선에 적용 할 수 있습니다.
정의 다각형의 볼록 껍질 내에있는 곡선 선입니다.