라인 생성 알고리즘

선은 두 점을 연결합니다. 그래픽의 기본 요소입니다. 선을 그리려면 선을 그릴 수있는 두 점이 필요합니다. 다음 세 가지 알고리즘에서 선의 한 지점을 $ X_ {0}, Y_ {0} $로, 두 번째 선의 지점을 $ X_ {1}, Y_ {1} $로 지칭합니다.

DDA 알고리즘

디지털 차동 분석기 (DDA) 알고리즘은 여기에서 단계별로 설명하는 간단한 라인 생성 알고리즘입니다.

Step 1 − 두 끝점 $ (X_ {0}, Y_ {0}) $ 및 $ (X_ {1}, Y_ {1}) $의 입력을 가져옵니다.

Step 2 − 두 끝점 간의 차이를 계산합니다.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3− 2 단계에서 계산 된 차이를 기준으로 픽셀을 넣을 단계 수를 식별해야합니다. dx> dy이면 x 좌표에 더 많은 단계가 필요합니다. 그렇지 않으면 y 좌표에서.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 − x 좌표와 y 좌표의 증분을 계산합니다.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 − 그에 따라 x 및 y 좌표를 성공적으로 증가시켜 픽셀을 배치하고 선 그리기를 완료합니다.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham의 라인 생성

Bresenham 알고리즘은 또 다른 증분 스캔 변환 알고리즘입니다. 이 알고리즘의 가장 큰 장점은 정수 계산 만 사용한다는 것입니다. 단위 간격으로 x 축을 가로 질러 이동하고 각 단계에서 두 개의 서로 다른 y 좌표 중에서 선택합니다.

예를 들어, 다음 그림과 같이 위치 (2, 3)에서 (3, 3) 및 (3, 4) 중에서 선택해야합니다. 원래 선에 더 가까운 점을 원합니다.

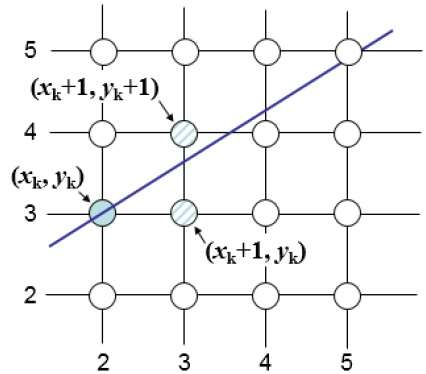
샘플 위치 $ X_ {k} + 1, $에서 수학적 선과의 수직 분리는 $ d_ {upper} $ 및 $ d_ {lower} $로 표시됩니다.

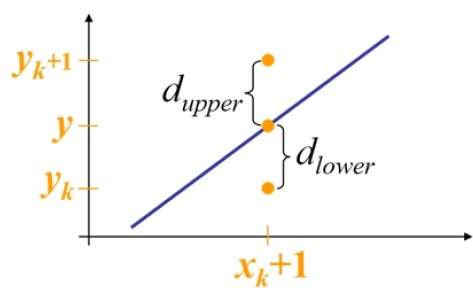
위 그림에서 $ x_ {k} + 1 $에있는 수학 선의 y 좌표는 −

Y = m ($ X_ {k} $ + 1) + b

따라서 $ d_ {upper} $ 및 $ d_ {lower} $는 다음과 같이 주어집니다.

$$ d_ {lower} = y-y_ {k} $$

$$ = m (X_ {k} + 1) + b-Y_ {k} $$

과

$$ d_ {upper} = (y_ {k} + 1)-y $$

$ = Y_ {k} + 1-m (X_ {k} + 1)-b $

이를 사용하여 어떤 픽셀이 수학적 선에 더 가까운 지에 대한 간단한 결정을 내릴 수 있습니다. 이 간단한 결정은 두 픽셀 위치의 차이를 기반으로합니다.

$$ d_ {lower}-d_ {upper} = 2m (x_ {k} + 1)-2y_ {k} + 2b-1 $$

m 을 dy / dx 로 대체하겠습니다. 여기서 dx 와 dy 는 끝점 간의 차이입니다.

$$ dx (d_ {lower}-d_ {upper}) = dx (2 \ frac {\ mathrm {d} y} {\ mathrm {d} x} (x_ {k} + 1)-2y_ {k} + 2b-1) $$

$$ = 2dy.x_ {k}-2dx.y_ {k} + 2dy + 2dx (2b-1) $$

$$ = 2dy.x_ {k}-2dx.y_ {k} + C $$

따라서 선을 따라 k 번째 단계에 대한 결정 매개 변수 $ P_ {k} $는 다음 과 같이 주어집니다.

$$ p_ {k} = dx (d_ {lower}-d_ {upper}) $$

$$ = 2dy.x_ {k}-2dx.y_ {k} + C $$

결정 매개 변수 $ P_ {k} $의 부호는 $ d_ {lower}-d_ {upper} $의 부호와 동일합니다.

$ p_ {k} $가 음수이면 아래쪽 픽셀을 선택하고 그렇지 않으면 위쪽 픽셀을 선택합니다.

좌표 변경은 단위 단계에서 x 축을 따라 발생하므로 정수 계산으로 모든 작업을 수행 할 수 있습니다. 단계 k + 1에서 결정 매개 변수는 다음과 같이 주어집니다.

$$ p_ {k +1} = 2dy.x_ {k + 1}-2dx.y_ {k + 1} + C $$

여기에서 $ p_ {k} $를 빼면-

$$ p_ {k + 1}-p_ {k} = 2dy (x_ {k + 1}-x_ {k})-2dx (y_ {k + 1}-y_ {k}) $$

하지만 $ x_ {k + 1} $는 $ (xk) + 1 $와 같습니다. 그래서-

$$ p_ {k + 1} = p_ {k} + 2dy-2dx (y_ {k + 1}-y_ {k}) $$

여기서 $ Y_ {k + 1} – Y_ {k} $는 $ P_ {k} $의 부호에 따라 0 또는 1입니다.

첫 번째 결정 매개 변수 $ p_ {0} $는 $ (x_ {0}, y_ {0}) $에서 평가됩니다.

$$ p_ {0} = 2dy-dx $$

이제 위의 모든 점과 계산을 염두에두고 기울기 m <1에 대한 Bresenham 알고리즘이 있습니다.

Step 1 − 왼쪽 끝점을 $ (x_ {0}, y_ {0}) $에 저장하여 두 줄의 끝점을 입력합니다.

Step 2 − 점 $ (x_ {0}, y_ {0}) $를 플로팅합니다.

Step 3 − 상수 dx, dy, 2dy 및 (2dy – 2dx)를 계산하고 결정 매개 변수의 첫 번째 값을 다음과 같이 구합니다.

$$ p_ {0} = 2dy-dx $$

Step 4 − k = 0에서 시작하여 선을 따라 각 $ X_ {k} $에서 다음 테스트를 수행합니다. −

$ p_ {k} $ <0이면 플롯 할 다음 점은 $ (x_ {k} +1, y_ {k}) $이고

$$ p_ {k + 1} = p_ {k} + 2dy $$ 그렇지 않으면

$$ (x_ {k}, y_ {k} +1) $$

$$ p_ {k + 1} = p_ {k} + 2dy-2dx $$

Step 5 − 4 단계 (dx – 1)를 반복합니다.

m> 1의 경우, 매번 y를 증가시키면서 x를 증가시켜야하는지 확인하십시오.

해결 후 결정 매개 변수 $ P_ {k} $의 방정식은 매우 유사하며 방정식의 x와 y 만 서로 바뀝니다.

중간 점 알고리즘

중간 점 알고리즘은 Pitteway와 Van Aken이 수정 한 Bresenham 때문입니다. 다음 그림과 같이 점 P를 (x, y) 좌표에 이미 놓고 선의 기울기가 0 ≤ k ≤ 1이라고 가정합니다.

이제 다음 점을 E 또는 N에 배치할지 여부를 결정해야합니다. 이것은 점 N 또는 E에 가장 가까운 교차점 Q를 식별하여 선택할 수 있습니다. 교차점 Q가 점 N에 가장 가까운 경우 N은 다음과 같이 간주됩니다. 다음 요점; 그렇지 않으면 E.

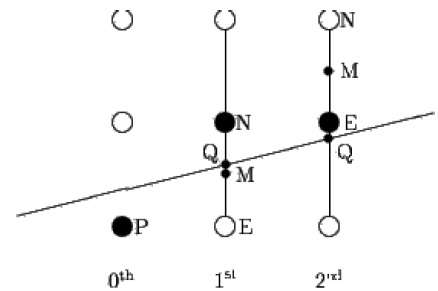
이를 결정하려면 먼저 중간 점 M (x + 1, y + ½)을 계산합니다. E와 N을 연결하는 수직선이있는 선의 교차점 Q가 M 미만이면 E를 다음 점으로 취합니다. 그렇지 않으면 N을 다음 점으로 취하십시오.

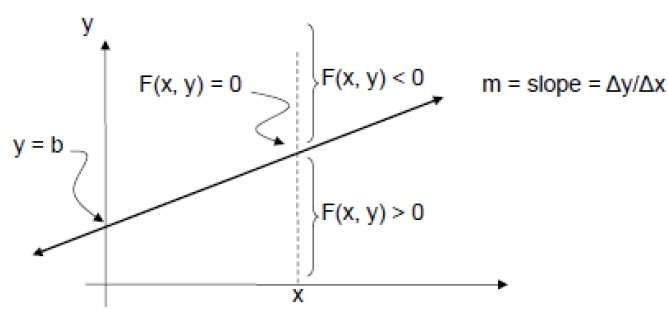
이를 확인하기 위해 암시 적 방정식을 고려해야합니다.

F (x, y) = mx + b-y

주어진 X에서 양의 m에 대해

y가 라인에 있으면 F (x, y) = 0
y가 선 위에 있으면 F (x, y) <0
y가 선 아래에 있으면 F (x, y)> 0