컴퓨터 그래픽 프랙탈
프랑스 / 미국의 수학자 Benoit Mandelbrot 박사가 프랙탈을 발견했습니다. 프랙탈이라는 단어는 부서짐 을 의미 하는 라틴어 프랙 터스 에서 파생되었습니다 .
프랙탈은 무엇입니까?
프랙탈은 컴퓨터가 단일 공식으로 생성 한 매우 복잡한 그림입니다. 반복을 사용하여 생성됩니다. 이는 이전 반복의 결과를 고려하여 하나의 수식이 약간 다른 값으로 반복해서 반복됨을 의미합니다.
프랙탈은 다음과 같은 많은 영역에서 사용됩니다.
Astronomy − 은하, 토성의 고리 등을 분석합니다.
Biology/Chemistry − 박테리아 배양, 화학 반응, 인체 해부학, 분자, 식물,
Others − 구름, 해안선 및 경계선, 데이터 압축, 확산, 경제, 프랙탈 아트, 프랙탈 음악, 풍경, 특수 효과 등을 묘사합니다.

프랙탈 생성
다음 그림과 같이 동일한 모양을 반복해서 반복하여 프랙탈을 생성 할 수 있습니다. 그림 (a)는 정삼각형을 보여줍니다. 그림 (b)에서 삼각형이 반복되어 별 모양을 만드는 것을 볼 수 있습니다. 그림 (c)에서 그림 (b)의 별 모양이 반복해서 반복되어 새로운 모양이 만들어지는 것을 볼 수 있습니다.
원하는 모양을 만들기 위해 무제한 반복을 수행 할 수 있습니다. 프로그래밍 용어에서 재귀는 이러한 모양을 만드는 데 사용됩니다.

기하학적 프랙탈
기하학적 프랙탈은 정수 또는 프랙탈 차원이 아닌 자연에서 발견되는 모양을 다룹니다. 결정 론적 (비 랜덤) 자기 유사 프랙탈을 기하학적으로 구성하기 위해, 우리는initiator. 이니시에이터의 하위 부분은 다음 패턴으로 대체됩니다.generator.

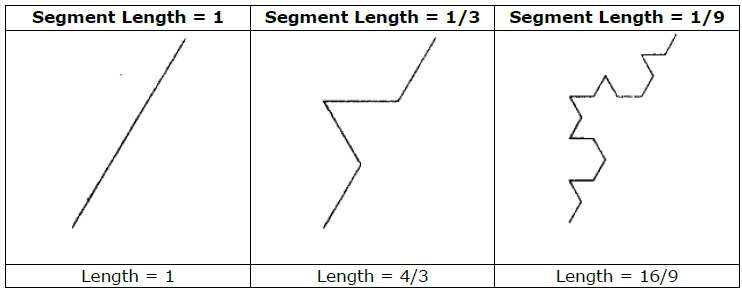
예를 들어 위의 그림과 같은 이니시에이터와 제너레이터를 사용하면 반복하여 좋은 패턴을 만들 수 있습니다. 이니시에이터의 각 직선 세그먼트는 각 단계에서 동일한 길이의 선 세그먼트 4 개로 대체됩니다. 배율 인수는 1/3이므로 프랙탈 차원은 D = ln 4 / ln 3 ≈ 1.2619입니다.
또한 이니시에이터의 각 선분의 길이는 각 단계에서 4/3 씩 증가하므로 다음 그림과 같이 곡선에 더 많은 세부 사항이 추가됨에 따라 프랙탈 곡선의 길이가 무한대가되는 경향이 있습니다.