디지털 통신-델타 변조
더 나은 샘플링을 얻으려면 신호의 샘플링 속도가 Nyquist 속도보다 높아야합니다. 차동 PCM에서이 샘플링 간격이 상당히 줄어들면 샘플 간 진폭 차이가 매우 작습니다.1-bit quantization, 그러면 스텝 크기가 매우 작아집니다. Δ (델타).
델타 변조
샘플링 속도가 훨씬 더 높고 양자화 후 단계 화가 더 작은 값인 변조 유형 Δ, 이러한 변조는 다음과 같이 불립니다. delta modulation.
델타 변조의 특징
다음은 델타 변조의 몇 가지 기능입니다.
신호 상관 관계를 최대한 활용하기 위해 오버 샘플링 된 입력이 사용됩니다.
양자화 설계는 간단합니다.
입력 시퀀스는 Nyquist 속도보다 훨씬 높습니다.
품질이 적당합니다.
변조기와 복조기의 설계는 간단합니다.
출력 파형의 계단식 근사치입니다.
스텝 크기는 매우 작습니다. Δ (델타).
비트 전송률은 사용자가 결정할 수 있습니다.
여기에는 더 간단한 구현이 포함됩니다.
델타 변조는 DPCM 기술의 단순화 된 형태로, 1-bit DPCM scheme. 샘플링 간격이 줄어들면 신호 상관 관계가 높아집니다.
델타 변조기
Delta Modulator는 1 비트 양자화 기 및 지연 회로와 2 개의 여름 회로로 구성됩니다. 다음은 델타 변조기의 블록 다이어그램입니다.
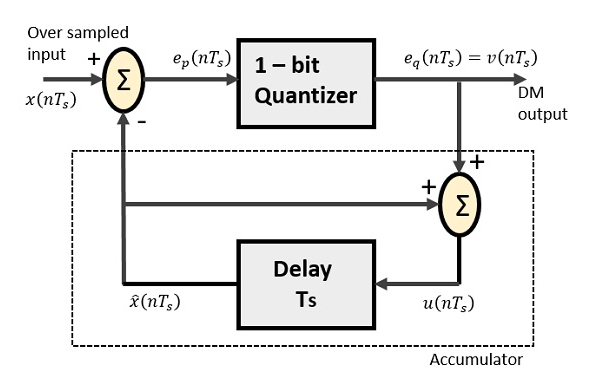
DPCM의 예측 회로는 DM의 간단한 지연 회로로 대체됩니다.
위의 다이어그램에서 다음과 같은 표기법이 있습니다.
$ x (nT_ {s}) $ = 오버 샘플링 된 입력
$ e_ {p} (nT_ {s}) $ = 여름 출력 및 양자화 기 입력
$ e_ {q} (nT_ {s}) $ = 양자화 기 출력 = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = 지연 회로 출력
$ u (nT_ {s}) $ = 지연 회로 입력
이 표기법을 사용하여 이제 우리는 델타 변조의 과정을 알아 내려고 노력할 것입니다.
$ e_ {p} (nT_ {s}) = x (nT_ {s})-\ widehat {x} (nT_ {s}) $
--------- 등식 1
$ = x (nT_ {s})-u ([n-1] T_ {s}) $
$ = x (nT_ {s})-[\ widehat {x} [[n-1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- 등식 2
더욱이,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- 등식 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
어디,
$ \ widehat {x} (nT_ {s}) $ = 지연 회로의 이전 값
$ e_ {q} (nT_ {s}) $ = 양자화 기 출력 = $ v (nT_s) $
그 후,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- 방정식 4
즉,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
누적 조건이 0이라고 가정하면,
$ u (nT_ {s}) = S \ displaystyle \ sum \ limits_ {j = 1} ^ n 시그 [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_ {s}) $
--------- 등식 5
이제
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ displaystyle \ sum \ limits_ {j = 1} ^ {n-1} v (jT_ {s}) $
--------- 방정식 6
지연 단위 출력은 하나의 샘플만큼 지연되는 누산기 출력입니다.
방정식 5와 6에서 복조기에 대한 가능한 구조를 얻습니다.
계단 형 근사 파형은 스텝 크기가 델타 () 인 델타 변조기의 출력이됩니다.Δ). 파형의 출력 품질이 보통입니다.
델타 복조기
델타 복조기는 저역 통과 필터, 서머 및 지연 회로로 구성됩니다. 여기서 예측 회로는 제거되므로 복조기에 가정 된 입력이 제공되지 않습니다.
다음은 델타 복조기의 다이어그램입니다.
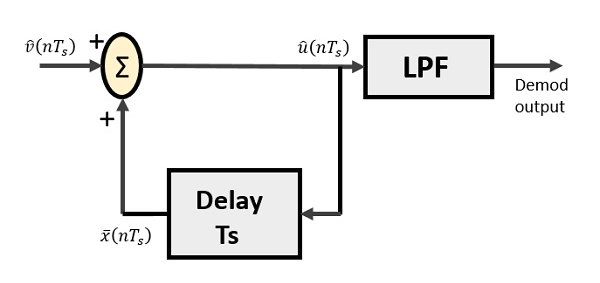
위의 다이어그램에서 다음과 같은 표기법이 있습니다.
$ \ widehat {v} (nT_ {s}) $는 입력 샘플입니다.
$ \ widehat {u} (nT_ {s}) $는 여름 출력입니다.
$ \ bar {x} (nT_ {s}) $는 지연된 출력입니다.
이진 시퀀스는 복조기에 대한 입력으로 제공됩니다. 계단식 근사 출력은 LPF에 제공됩니다.
저역 통과 필터는 여러 가지 이유로 사용되지만 두드러진 이유는 대역 외 신호에 대한 노이즈 제거입니다. 송신기에서 발생할 수있는 단계 크기 오류를granular noise, 여기에서 제거됩니다. 잡음이없는 경우 변조기 출력은 복조기 입력과 같습니다.
DPCM 대비 DM의 장점
1 비트 양자화 기
변조기와 복조기의 매우 쉬운 설계
그러나 DM에는 약간의 소음이 있습니다.
기울기 과부하 왜곡 ( Δ 작다)
세분화 된 노이즈 ( Δ 크다)
적응 형 델타 변조 (ADM)
디지털 변조에서 우리는 출력 파의 품질에 영향을 미치는 스텝 크기를 결정하는 특정 문제를 발견했습니다.
변조 신호의 가파른 기울기에서는 더 큰 스텝 크기가 필요하고 메시지의 기울기가 작은 경우 더 작은 스텝 크기가 필요합니다. 그 과정에서 세부 사항이 누락됩니다. 따라서 원하는 방식으로 샘플링을 얻기 위해 요구 사항에 따라 스텝 크기 조정을 제어 할 수 있다면 더 좋을 것입니다. 이것은의 개념입니다Adaptive Delta Modulation.
다음은 적응 형 델타 변조기의 블록 다이어그램입니다.
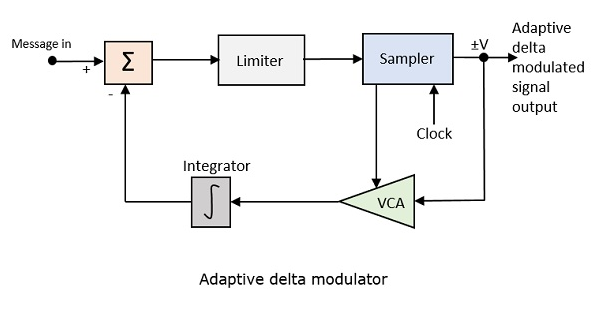
전압 제어 증폭기의 이득은 샘플러의 출력 신호에 의해 조정됩니다. 증폭기 이득은 스텝 크기를 결정하며 둘 다 비례합니다.
ADM은 현재 샘플의 값과 다음 샘플의 예측 값 간의 차이를 양자화합니다. 빠르게 변화하는 값을 충실하게 재현하기 위해 가변 단계 높이를 사용하여 다음 값을 예측합니다.