디지털 통신-샘플링
Sampling "연속 시간 신호의 순간 값을 이산 형태로 측정하는 과정"으로 정의됩니다.
Sample 시간 영역에서 연속적인 전체 데이터에서 가져온 데이터 조각입니다.
소스가 아날로그 신호를 생성 할 때 디지털화해야하는 경우 1s 과 0s즉, 높음 또는 낮음, 신호는 시간에 따라 이산화되어야합니다. 이러한 아날로그 신호의 이산화를 샘플링이라고합니다.
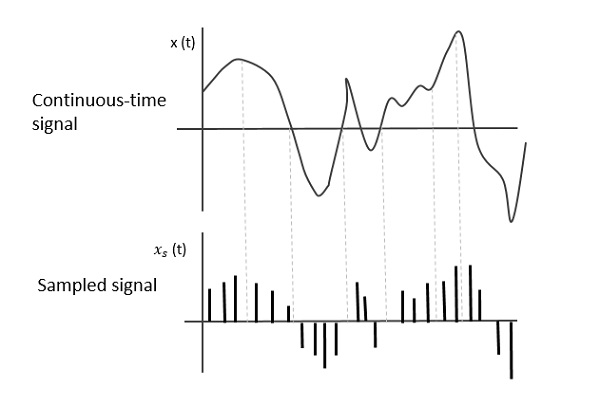
다음 그림은 연속 시간 신호를 나타냅니다. x (t) 및 샘플링 된 신호 xs (t). 언제x (t) 주기적인 임펄스 트레인, 샘플링 된 신호를 곱합니다. xs (t) 획득됩니다.
샘플링 속도
신호를 이산화하려면 샘플 간의 간격을 수정해야합니다. 그 격차는sampling period Ts.
$$ 샘플링 \ : 주파수 = \ frac {1} {T_ {s}} = f_s $$어디,
$ T_ {s} $는 샘플링 시간입니다.
$ f_ {s} $는 샘플링 주파수 또는 샘플링 속도입니다.
Sampling frequency샘플링 기간의 역수입니다. 이 샘플링 주파수는 간단히 다음과 같이 부를 수 있습니다.Sampling rate. 샘플링 속도는 초당 또는 유한 한 값 집합에 대해 취한 샘플 수를 나타냅니다.
디지털화 된 신호에서 아날로그 신호를 재구성하려면 샘플링 속도를 고려해야합니다. 샘플링 속도는 메시지 신호의 데이터가 손실되거나 겹치지 않아야합니다. 따라서 Nyquist rate라고하는 요금이 고정되었습니다.
나이 퀴 스트 비율
신호가 다음보다 높은 주파수 성분없이 대역 제한이라고 가정합니다. W헤르츠. 그것의 의미는,W가장 높은 주파수입니다. 이러한 신호의 경우 원래 신호를 효과적으로 재생하려면 샘플링 속도가 최고 주파수의 두 배 여야합니다.
즉,
$$ f_ {S} = 2 주 $$어디,
$ f_ {S} $는 샘플링 속도입니다.
W 가장 높은 주파수
이 샘플링 속도를 Nyquist rate.
이 나이 퀴 스트 비율 이론에 대해 샘플링 정리라는 정리가 언급되었습니다.
샘플링 정리
다음과 같이 불리는 샘플링 정리 Nyquist theorem, 대역폭이 제한된 함수 클래스에 대한 대역폭 측면에서 충분한 샘플 속도 이론을 제공합니다.
샘플링 정리는 다음과 같이 말합니다.“신호가 속도로 샘플링되면 정확하게 재현 될 수 있습니다. fs 최대 주파수의 두 배보다 큽니다. W.”
이 샘플링 정리를 이해하기 위해 대역 제한 신호, 즉 값이 다음과 같은 신호를 고려해 보겠습니다. non-zero 일부 사이 –W 과 W 헤르츠.
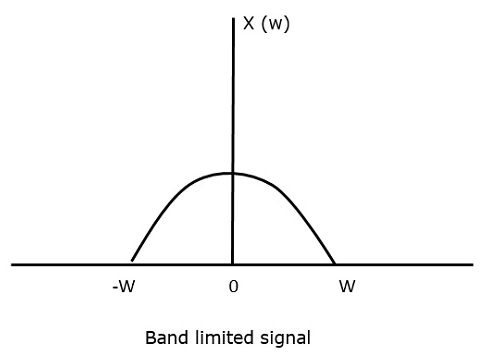
이러한 신호는 다음과 같이 표현됩니다. $x(f) = 0 for |f\lvert > W$
연속 시간 신호용 x (t)주파수 영역에서 대역 제한 신호 인는 다음 그림과 같이 나타낼 수 있습니다.
샘플링 후에도 정보 손실이 없어야하는 샘플링 주파수가 필요합니다. 이를 위해 샘플링 주파수가 최대 주파수의 두 배가되어야하는 나이 퀴 스트 속도가 있습니다. 샘플링의 임계 비율입니다.
신호가 x(t) Nyquist 속도 이상으로 샘플링되면 원래 신호를 복구 할 수 있으며 Nyquist 속도 미만으로 샘플링하면 신호를 복구 할 수 없습니다.
다음 그림은 다음보다 높은 속도로 샘플링 된 경우 신호를 설명합니다. 2w 주파수 영역에서.
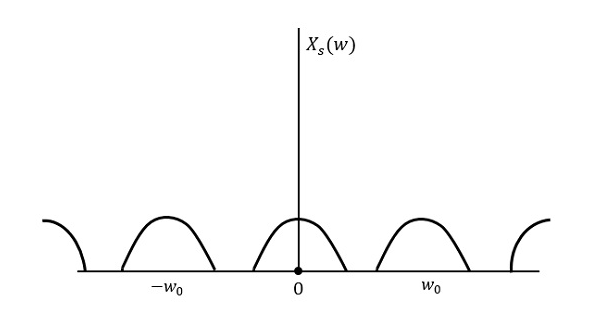
위 그림은 신호의 푸리에 변환을 보여줍니다. $x_{s}(t)$. 여기서 정보는 손실없이 재생산됩니다. 혼동이 없으므로 복구가 가능합니다.
신호의 푸리에 변환 $x_{s}(t)$ 이다
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n =-\ infty} ^ \ infty X (w-nw_0) $$$ T_ {s} $ = Sampling Period 및 $ w_ {0} = \ frac {2 \ pi} {T_s} $
샘플링 속도가 가장 높은 주파수의 두 배 (2W)
그것의 의미는,
$$ f_ {s} = 2 주 $$어디,
$ f_ {s} $는 샘플링 빈도입니다.
W 가장 높은 주파수
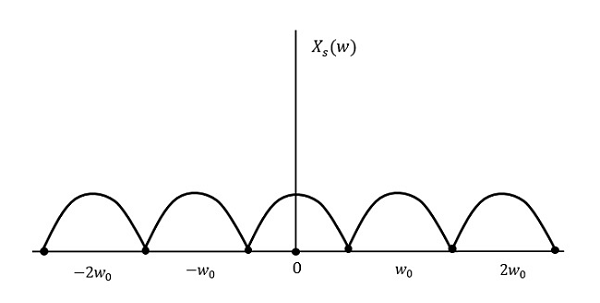
결과는 위 그림과 같습니다. 정보는 손실없이 교체됩니다. 따라서 이것은 또한 좋은 샘플링 속도입니다.
이제 조건을 살펴 보겠습니다.
$$ f_ {s} <2W $$결과 패턴은 다음 그림과 같습니다.

위의 패턴에서 정보의 겹침이 발생하여 정보의 혼동과 손실이 발생 함을 알 수 있습니다. 이러한 원치 않는 중복 현상을 앨리어싱이라고합니다.
앨리어싱
앨리어싱은 "샘플링 된 버전의 스펙트럼에서 저주파 성분의 식별을 취하는 신호 스펙트럼의 고주파 성분 현상"이라고 할 수 있습니다.
앨리어싱의 영향을 줄이기 위해 취한 시정 조치는 다음과 같습니다.
PCM의 송신기 섹션에서 low pass anti-aliasing filter 원치 않는 고주파 성분을 제거하기 위해 샘플러 전에 사용됩니다.
필터링 후 샘플링 된 신호는 나이 퀴 스트 속도보다 약간 높은 속도로 샘플링됩니다.
Nyquist 속도보다 높은 샘플링 속도를 선택하면 reconstruction filter 수신기에서.
푸리에 변환의 범위
일반적으로 신호를 분석하고 정리를 증명할 때 푸리에 급수 및 푸리에 변환의 도움을 구하는 것으로 관찰됩니다. 왜냐하면-
푸리에 변환은 비 주기적 신호에 대한 푸리에 시리즈의 확장입니다.
푸리에 변환은 서로 다른 도메인의 신호를 확인하고 신호를 쉽게 분석하는 데 도움이되는 강력한 수학적 도구입니다.
이 푸리에 변환을 사용하여 사인과 코사인의 합으로 모든 신호를 분해 할 수 있습니다.
다음 장에서는 양자화 개념에 대해 논의하겠습니다.