디지털 통신-라인 코드
ㅏ line code전송 라인을 통한 디지털 신호의 데이터 전송에 사용되는 코드입니다. 이 코딩 프로세스는 심볼 간 간섭과 같은 신호의 겹침 및 왜곡을 피하기 위해 선택됩니다.
라인 코딩의 속성
다음은 라인 코딩의 속성입니다-
단일 신호에서 더 많은 비트를 전송하기 위해 코딩이 수행되므로 사용되는 대역폭이 훨씬 줄어 듭니다.
주어진 대역폭에 대해 전력이 효율적으로 사용됩니다.
오류 가능성이 훨씬 줄어 듭니다.
오류 감지가 수행되고 양극성에도 수정 기능이 있습니다.
전력 밀도는 훨씬 유리합니다.
타이밍 내용이 적절합니다.
긴 문자열 1s 과 0s 투명성을 유지하기 위해 피합니다.
라인 코딩 유형
Line Coding에는 3 가지 유형이 있습니다.
- Unipolar
- Polar
- Bi-polar
단극 신호
단극 신호는 On-Off Keying 또는 간단히 OOK.
맥박의 존재는 1 맥박의 부재는 0.
단극 신호에는 두 가지 변형이 있습니다.
- NRZ (Non Return to Zero)
- 제로로 돌아 가기 (RZ)
유니 폴라 NRZ (Non-Return to Zero)
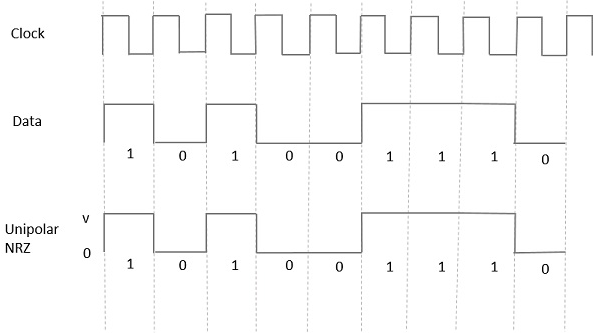
이러한 유형의 단극 신호에서 높은 데이터는 다음과 같은 양의 펄스로 표시됩니다. Mark, 기간이 있습니다. T0심볼 비트 기간과 같습니다. 낮은 데이터 입력에는 펄스가 없습니다.
다음 그림은이를 명확하게 보여줍니다.
Advantages
Unipolar NRZ의 장점은 다음과 같습니다.
- 이건 간단하다.
- 더 적은 대역폭이 필요합니다.
Disadvantages
Unipolar NRZ의 단점은 다음과 같습니다.
오류 수정이 수행되지 않았습니다.
저주파 구성 요소가 있으면 신호가 늘어날 수 있습니다.
시계가 없습니다.
동기화 손실이 발생할 수 있습니다 (특히 긴 문자열의 경우). 1s 과 0s).
단극 제로 복귀 (RZ)
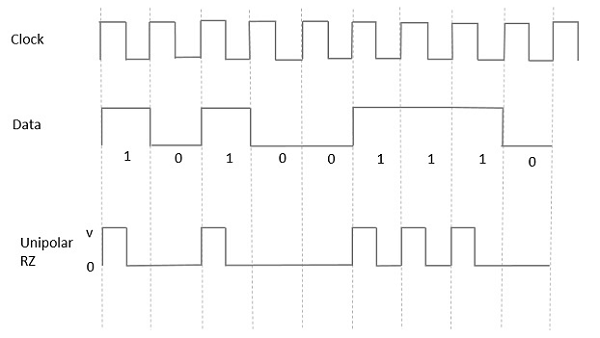
이러한 유형의 단극 시그널링에서 높은 데이터는 Mark pulse, 기간 T0심볼 비트 기간보다 작습니다. 비트 지속 시간의 절반은 높게 유지되지만 즉시 0으로 돌아가 나머지 비트 지속 시간 동안 펄스가 없음을 나타냅니다.
다음 그림의 도움으로 명확하게 이해됩니다.
Advantages
Unipolar RZ의 장점은 다음과 같습니다.
- 이건 간단하다.
- 심볼 레이트에 존재하는 스펙트럼 라인은 클럭으로 사용될 수 있습니다.
Disadvantages
Unipolar RZ의 단점은 다음과 같습니다.
- 오류 수정이 없습니다.
- 단극 NRZ보다 2 배의 대역폭을 차지합니다.
- 신호 드룹은 신호가 0Hz에서 0이 아닌 곳에서 발생합니다.
극지 신호
Polar Signaling에는 두 가지 방법이 있습니다. 그들은-
- 극지 NRZ
- 극지 RZ
극지 NRZ
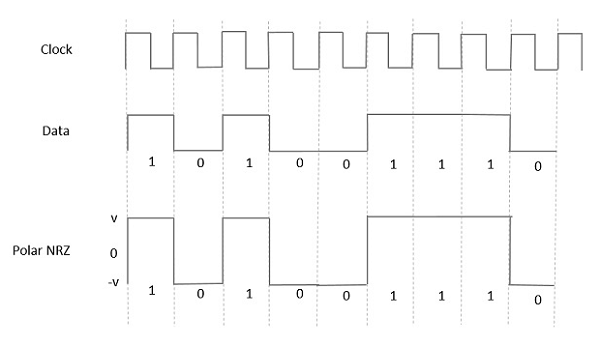
이러한 유형의 Polar 신호에서 High in 데이터는 양의 펄스로 표시되고 Low in 데이터는 음의 펄스로 표시됩니다. 다음 그림은이를 잘 보여줍니다.
Advantages
Polar NRZ의 장점은 다음과 같습니다.
- 이건 간단하다.
- 저주파 구성 요소가 없습니다.
Disadvantages
Polar NRZ의 단점은 다음과 같습니다.
오류 수정이 없습니다.
시계가 없습니다.
신호 드룹은 신호가 0이 아닌 곳에서 발생합니다. 0 Hz.
극지 RZ
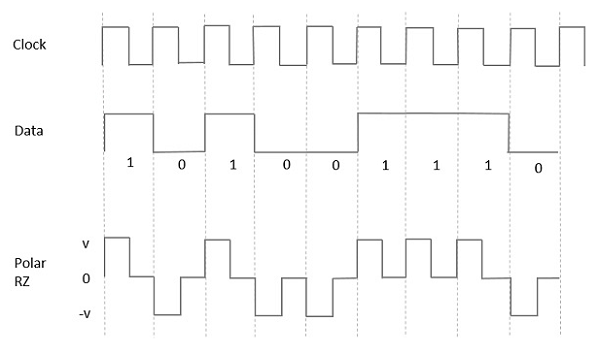
이러한 유형의 극성 신호에서 데이터가 높음 Mark pulse, 기간 T0심볼 비트 기간보다 작습니다. 비트 지속 시간의 절반은 높게 유지되지만 즉시 0으로 돌아가 나머지 비트 지속 시간 동안 펄스가 없음을 나타냅니다.
그러나 Low 입력의 경우 음의 펄스는 데이터를 나타내고 0 레벨은 비트 지속 시간의 나머지 절반 동안 동일하게 유지됩니다. 다음 그림은이를 명확하게 보여줍니다.
Advantages
Polar RZ의 장점은 다음과 같습니다.
- 이건 간단하다.
- 저주파 구성 요소가 없습니다.
Disadvantages
Polar RZ의 단점은 다음과 같습니다.
오류 수정이 없습니다.
시계가 없습니다.
Polar NRZ 대역폭의 두 배를 차지합니다.
신호 드룹은 신호가 0이 아닌 곳에서 발생합니다. 0 Hz.
양극성 신호
이것은 세 가지 전압 레벨 즉, +, - 과 0. 이러한 신호를 다음과 같이 호출합니다.duo-binary signal.
이 유형의 예는 다음과 같습니다. Alternate Mark Inversion (AMI). 에 대한1, 전압 레벨은 +에서 – 또는 –에서 +로 전환됩니다. 1s같은 극성이어야합니다. ㅏ0 전압 레벨이 0이됩니다.
이 방법에서도 두 가지 유형이 있습니다.
- 양극성 NRZ
- 양극성 RZ
지금까지 논의한 모델에서 NRZ와 RZ의 차이점을 배웠습니다. 여기에서도 같은 방식으로 진행됩니다. 다음 그림은이를 명확하게 보여줍니다.
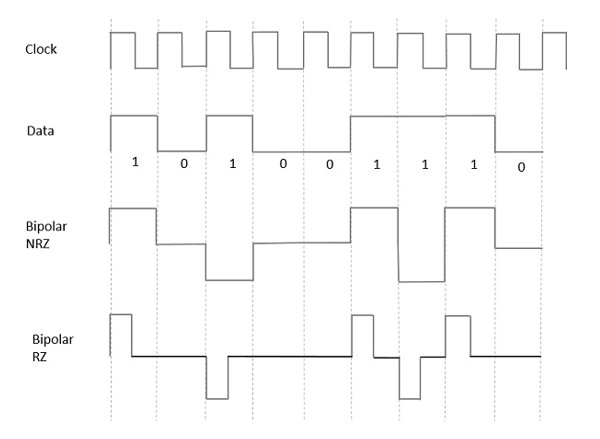
위의 그림에는 바이폴라 NRZ 및 RZ 파형이 모두 있습니다. 펄스 지속 시간과 심볼 비트 지속 시간은 NRZ 유형에서 동일하지만 펄스 지속 시간은 RZ 유형에서 심볼 비트 지속 시간의 절반입니다.
장점
다음은 장점입니다-
이건 간단하다.
저주파 구성 요소가 없습니다.
유니 폴라 및 폴라 NRZ 방식보다 낮은 대역폭을 차지합니다.
이 기술은 여기에서 신호 처짐이 발생하지 않기 때문에 AC 결합 라인을 통한 전송에 적합합니다.
여기에는 단일 오류 감지 기능이 있습니다.
단점
다음은 단점입니다-
- 시계가 없습니다.
- 데이터 문자열이 길면 동기화가 손실됩니다.
전력 스펙트럼 밀도
주파수 영역에서 신호의 전력이 다양한 주파수에서 어떻게 분산되는지를 설명하는 함수를 다음과 같이 호출합니다. Power Spectral Density (PSD).
PSD는 자동 상관의 푸리에 변환입니다 (관측치 간의 유사성). 그것은 직사각형 펄스의 형태입니다.
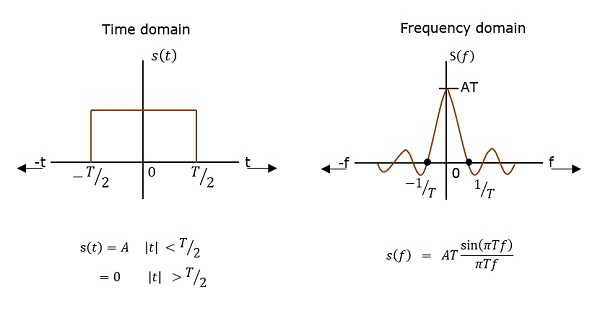
PSD 파생
Einstein-Wiener-Khintchine 정리에 따르면 임의 프로세스의 자기 상관 함수 또는 전력 스펙트럼 밀도를 알고 있으면 다른 하나를 정확하게 찾을 수 있습니다.
따라서 전력 스펙트럼 밀도를 도출하기 위해 아래와 같이 전력 신호 $ x (t) $의 시간 자동 상관 $ (R_x (\ tau)) $를 사용할 것입니다.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{-T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
$ x (t) $는 임펄스로 구성되어 있으므로 $ R_x (\ tau) $는 다음과 같이 쓸 수 있습니다.
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limits_ {n =-\ infty} ^ \ infty R_n \ delta (\ tau-nT) $
$ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
실제 신호에 대해 $ R_n = R _ {-n} $을 알면
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
펄스 필터의 스펙트럼은 $ (w) \ leftrightarrow f (t) $이므로
$ s_y (w) = \ mid F (w) \ mid ^ 2S_x (w) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limits_ {n =-\ infty} ^ \ infty R_ne ^ {-jnwT_ {b}}) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
따라서 전력 스펙트럼 밀도에 대한 방정식을 얻습니다. 이를 사용하여 다양한 라인 코드의 PSD를 찾을 수 있습니다.