소스 코딩 정리

메모리가없는 개별 소스에서 생성 된 코드는 효율적으로 표현되어야하며 이는 통신에서 중요한 문제입니다. 이를 위해 이러한 소스 코드를 나타내는 코드 단어가 있습니다.

예를 들어 전신에서 우리는 알파벳이 다음과 같이 표시되는 모스 부호를 사용합니다. Marks 과 Spaces. 편지가E 주로 사용되는 것으로 간주되며 다음과 같이 표시됩니다. “.” 반면 편지는 Q 거의 사용되지 않으며 다음과 같이 표시됩니다. “--.-”

블록 다이어그램을 살펴 보겠습니다.

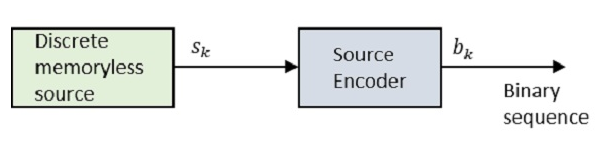
어디 S_k 이산 메모리리스 소스의 출력이며 b_k 다음으로 표시되는 소스 인코더의 출력입니다. 0s 과 1s.

인코딩 된 시퀀스는 수신기에서 편리하게 디코딩됩니다.

소스에 알파벳이 있다고 가정합시다. k 다른 기호와 그 k^th 상징 S_k 확률로 발생 P_k, 어디 k = 0, 1…k-1.

이진 코드 단어를 기호에 할당하십시오. S_k, 길이가있는 인코더에 의해 l_k, 비트 단위로 측정됩니다.

따라서 소스 인코더 의 평균 코드 워드 길이 L 을 다음 과 같이 정의합니다.

$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$

L 소스 심볼 당 평균 비트 수를 나타냅니다.

$ L_ {min} = \ : 최소값 \ : 가능한 \ : 값 \ : of \ : \ overline {L} $

그때 coding efficiency 다음과 같이 정의 할 수 있습니다.

$$ \ eta = \ frac {L {min}} {\ overline {L}} $$

$ \ overline {L} \ geq L_ {min} $를 사용하면 $ \ eta \ leq 1 $가됩니다.

그러나 소스 인코더는 $ \ eta = 1 $ 일 때 효율적인 것으로 간주됩니다.

이를 위해 $ L_ {min} $ 값을 결정해야합니다.

우리가 정의를 참조하자 "엔트로피 $의 H (\ 델타) $, 평균 코드 워드 길이의 이산 무 메모리 소스 감안할 때L 모든 소스 인코딩은 $ \ overline {L} \ geq H (\ delta) $로 제한됩니다. "

간단히 말해서 코드 단어 (예 : QUEUE라는 단어의 모스 부호는 -.- ..-. ..-.)는 항상 소스 코드 (예 : QUEUE)보다 크거나 같습니다. 즉, 코드 단어의 기호가 소스 코드의 알파벳보다 크거나 같습니다.

따라서 $ L_ {min} = H (\ delta) $를 사용하면 엔트로피 $ H (\ delta) $ 측면에서 소스 인코더의 효율성을 다음과 같이 작성할 수 있습니다.

$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$

이 소스 코딩 정리는 noiseless coding theorem오류없는 인코딩을 설정합니다. 그것은 또한Shannon’s first theorem.