그래프 이론-커버링
커버링 그래프는 다른 그래프에 해당하는 모든 정점 또는 모든 모서리를 포함하는 하위 그래프입니다. 모든 꼭지점을 포함하는 하위 그래프를line/edge covering. 모든 모서리를 포함하는 하위 그래프를vertex covering.
라인 커버링
G = (V, E)를 그래프라고합시다. G의 모든 정점이 C에서 적어도 하나의 가장자리에 입사하는 경우 부분 집합 C (E)는 G의 선을 덮는 것입니다. 즉,
deg (V) ≥ 1 ∀ V ∈ G
각 꼭지점이 가장자리로 다른 꼭지점과 연결되어 있기 때문입니다. 따라서 최소 차수가 1입니다.
Example
다음 그래프를보세요-
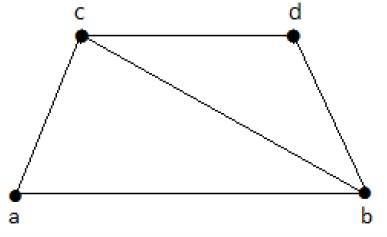
라인 커버링이있는 하위 그래프는 다음과 같습니다.
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
'G'의 선 커버는 'G'에 고립 된 꼭지점이있는 경우에만 존재하지 않습니다. 'n'개의 꼭지점이있는 그래프의 선 커버링에는 최소한 [n / 2] 개의 가장자리가 있습니다.
최소 라인 커버링
그래프 G의 C를 덮는 선은 최소라고합니다. if no edge can be deleted from C.
Example
위 그래프에서 선을 덮은 부분 그래프는 다음과 같습니다.
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
여기에서 C 1 , C 2 , C 3 은 최소한의 라인 커버링이지만 C 4 는 {b, c}를 삭제할 수 있기 때문에 그렇지 않습니다.
최소 라인 커버링
그것은 또한 알려져 있습니다 Smallest Minimal Line Covering. 최소한의 가장자리로 덮는 최소 선을 'G'의 최소 선 덮기라고합니다. 'G'를 덮는 최소 선의 모서리 수를line covering number of ‘G’ (α1).
Example
In the above example, C1 and C2 are the minimum line covering of G and α1 = 2.
Every line covering contains a minimal line covering.
Every line covering does not contain a minimum line covering (C3 does not contain any minimum line covering.
No minimal line covering contains a cycle.
If a line covering ‘C’ contains no paths of length 3 or more, then ‘C’ is a minimal line covering because all the components of ‘C’ are star graph and from a star graph, no edge can be deleted.
Vertex Covering
Let ‘G’ = (V, E) be a graph. A subset K of V is called a vertex covering of ‘G’, if every edge of ‘G’ is incident with or covered by a vertex in ‘K’.
Example
Take a look at the following graph −
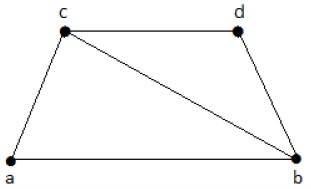
The subgraphs that can be derived from the above graph are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
K4 = {a, d}
Here, K1, K2, and K3 have vertex covering, whereas K4 does not have any vertex covering as it does not cover the edge {bc}.
Minimal Vertex Covering
A vertex ‘K’ of graph ‘G’ is said to be minimal vertex covering if no vertex can be deleted from ‘K’.
Example
In the above graph, the subgraphs having vertex covering are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
Here, K1 and K2 are minimal vertex coverings, whereas in K3, vertex ‘d’ can be deleted.
Minimum Vertex Covering
It is also known as the smallest minimal vertex covering. A minimal vertex covering of graph ‘G’ with minimum number of vertices is called the minimum vertex covering.
The number of vertices in a minimum vertex covering of ‘G’ is called the vertex covering number of G (α2).
Example
In the following graph, the subgraphs having vertex covering are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}

Here, K1 is a minimum vertex cover of G, as it has only two vertices. α2 = 2.