그래프 이론-퀵 가이드
수학 및 컴퓨터 과학 분야에서 그래프 이론은 모서리와 꼭지점 간의 관계와 관련된 그래프에 대한 연구입니다 . 컴퓨터 과학, 정보 기술, 생명 과학, 수학 및 언어학에 응용되는 인기있는 과목입니다. 더 이상 고민하지 않고 그래프 정의부터 시작하겠습니다.
그래프 란?
그래프는 일부 개체 쌍이 링크로 연결된 개체 집합을 그림으로 표현한 것입니다. 상호 연결된 개체는 다음과 같은 점으로 표현됩니다.vertices, 정점을 연결하는 링크가 호출됩니다. edges.
공식적으로 그래프는 한 쌍의 집합입니다. (V, E), 어디 V는 정점 세트이고 E는 정점 쌍을 연결하는 가장자리 세트입니다. 다음 그래프를보세요-
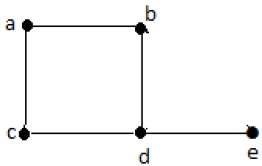
위 그래프에서
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
그래프 이론의 응용
그래프 이론은 다양한 엔지니어링 분야에 적용됩니다.
Electrical Engineering− 그래프 이론의 개념은 회로 연결 설계에 광범위하게 사용됩니다. 연결 유형 또는 구성은 토폴로지로 명명됩니다. 토폴로지의 몇 가지 예는 스타, 브리지, 직렬 및 병렬 토폴로지입니다.
Computer Science− 그래프 이론은 알고리즘 연구에 사용됩니다. 예를 들면
- Kruskal의 알고리즘
- 프림의 알고리즘
- Dijkstra의 알고리즘
Computer Network − 네트워크에서 상호 연결된 컴퓨터 간의 관계는 그래프 이론의 원리를 따릅니다.
Science − 물질의 분자 구조와 화학 구조, 유기체의 DNA 구조 등을 그래프로 표시합니다.
Linguistics − 언어의 구문 분석 트리와 언어의 문법은 그래프를 사용합니다.
General− 도시 간 경로를 그래프로 표시 할 수 있습니다. 가계도와 같은 계층 적 순서 정보를 묘사하는 것은 트리라는 특별한 유형의 그래프로 사용할 수 있습니다.
그래프는 점과 점에 연결된 선의 다이어그램입니다. 정점이 연결되지 않은 두 정점 집합을 연결하는 선이 하나 이상 있습니다. 그래프 이론에서 그래프의 개념은 점, 선, 꼭지점, 가장자리, 꼭지점의 정도, 그래프의 속성 등과 같은 몇 가지 기본 용어를 기반으로합니다. 여기이 장에서는 이러한 그래프 이론의 기본 사항을 다룹니다.
포인트
A point1 차원, 2 차원 또는 3 차원 공간의 특정 위치입니다. 더 나은 이해를 위해 점을 알파벳으로 표시 할 수 있습니다. 점으로 표시 할 수 있습니다.
예

여기서 점은 'a'라는 점입니다.
선
ㅏ Line두 지점 사이의 연결입니다. 실선으로 표시 할 수 있습니다.
Example

여기서 'a'와 'b'는 포인트입니다. 이 두 지점 사이의 연결을 선이라고합니다.
꼭지점
정점은 여러 선이 만나는 지점입니다. 그것은 또한node. 점과 유사하게 정점도 알파벳으로 표시됩니다.
Example

여기서 정점은 알파벳 'a'로 이름이 지정됩니다.
가장자리
모서리는 두 정점을 연결하는 선에 대한 수학적 용어입니다. 단일 정점에서 많은 모서리를 형성 할 수 있습니다. 꼭지점이 없으면 가장자리를 만들 수 없습니다. 가장자리에 대한 시작 꼭지점과 끝 꼭지점이 있어야합니다.
Example

여기서 'a'와 'b'는 두 꼭지점이며 이들 사이의 링크를 가장자리라고합니다.
그래프
그래프 'G'는 G = (V, E)로 정의됩니다. 여기서 V는 모든 꼭지점의 집합이고 E는 그래프의 모든 모서리 집합입니다.
Example 1

위의 예에서 ab, ac, cd 및 bd는 그래프의 간선입니다. 마찬가지로 a, b, c, d는 그래프의 꼭지점입니다.
Example 2
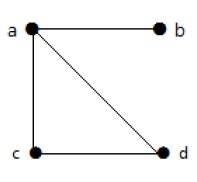
이 그래프에는 네 개의 꼭지점 a, b, c, d와 네 개의 모서리 ab, ac, ad, cd가 있습니다.
고리
그래프에서 가장자리가 꼭지점에서 그 자체로 그려지는 경우이를 루프라고합니다.
Example 1

위의 그래프에서 V는 루프를 형성하는 모서리 (V, V)가있는 정점입니다.
Example 2

이 그래프에는 꼭지점 a와 꼭지점 b에 형성된 두 개의 루프가 있습니다.
정점의 정도
정점 V에 인접한 정점의 수입니다.
Notation − deg (V).
n 개의 정점이있는 간단한 그래프에서 모든 정점의 차수는 다음과 같습니다.
deg (v) ≤ n – 1 ∀ v ∈ G
정점은 그 자체를 제외하고 다른 모든 정점과 함께 가장자리를 형성 할 수 있습니다. 따라서 정점의 정도는number of vertices in the graph minus 1. 이 1은 자체적으로 루프를 형성 할 수 없기 때문에 자체 정점 용입니다. 정점에 루프가있는 경우 단순 그래프가 아닙니다.
정점의 정도는 그래프의 두 가지 경우에서 고려할 수 있습니다.
무 방향 그래프
유향 그래프
무 방향 그래프의 정점 각도
무 방향 그래프에는 유 방향 간선이 없습니다. 다음 예를 고려하십시오.
Example 1
다음 그래프를보세요-

위의 무 방향 그래프에서
deg (a) = 2, 꼭지점 'a'에서 만나는 2 개의 모서리가 있기 때문입니다.
deg (b) = 3, 꼭지점 'b'에서 만나는 3 개의 가장자리가 있기 때문입니다.
deg (c) = 1, 꼭지점 'c'에 1 개의 모서리가 형성됨
그래서 'c'는 pendent vertex.
deg (d) = 2, 꼭지점 'd'에서 만나는 2 개의 가장자리가 있기 때문입니다.
deg (e) = 0, 꼭지점 'e'에 0 개의 가장자리가 있기 때문입니다.
그래서 'e'는 isolated vertex.
Example 2
다음 그래프를보세요-

위 그래프에서
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2, deg (e) = 0입니다.
꼭지점 'e'는 격리 된 꼭지점입니다. 그래프에는 늘어진 꼭지점이 없습니다.
유향 그래프의 꼭지점 각도
유 방향 그래프에서 각 정점에는 indegree 그리고 outdegree.
그래프의 정도
Indegree of vertex V는 꼭지점 V로 들어오는 가장자리의 수입니다.
Notation − deg− (V).
그래프의 이탈
Outdegree of vertex V는 꼭지점 V에서 나가는 가장자리의 수입니다.
Notation − deg + (V).
다음 예를 고려하십시오.
Example 1
다음 유향 그래프를 살펴보십시오. 꼭지점 'a'에는 바깥쪽으로가는 'ad'와 'ab'의 두 모서리가 있습니다. 따라서 그것의 outdegree는 2입니다. 마찬가지로, 꼭지점 'a'쪽으로 오는 가장자리 'ga'가 있습니다. 따라서 'a'의 정도는 1입니다.

다음 표는 다른 정점의 부도 및 외도를 보여줍니다.
| 꼭지점 | 맞지 않음 | 이상 |
|---|---|---|
| ㅏ | 1 | 2 |
| 비 | 2 | 0 |
| 씨 | 2 | 1 |
| 디 | 1 | 1 |
| 이자형 | 1 | 1 |
| 에프 | 1 | 1 |
| 지 | 0 | 2 |
Example 2
다음 유향 그래프를 살펴보십시오. 정점 'a'에는 정점 'a'에서 바깥쪽으로가는 가장자리 'ae'가 있습니다. 따라서 그 외각은 1입니다. 마찬가지로 그래프에는 정점 'a'를 향하는 가장자리 'ba'가 있습니다. 따라서 'a'의 정도는 1입니다.

다음 표는 다른 정점의 부도 및 외도를 보여줍니다.
| 꼭지점 | 맞지 않음 | 이상 |
|---|---|---|
| ㅏ | 1 | 1 |
| 비 | 0 | 2 |
| 씨 | 2 | 0 |
| 디 | 1 | 1 |
| 이자형 | 1 | 1 |
늘어진 꼭지점
정점의 각도를 사용하여 두 가지 특별한 유형의 정점을 갖게됩니다. 차수가 1 인 정점을 펜던트 정점이라고합니다.
Example

이 예에서 꼭지점 'a'와 꼭지점 'b'는 연결된 가장자리 'ab'를 갖습니다. 따라서 꼭지점 'a'에 대해서는 꼭지점 'b'를 향하는 가장자리가 하나 뿐이고 꼭지점 'b'에 대해서도 마찬가지로 꼭지점 'a'에 대한 가장자리가 하나뿐입니다. 마지막으로 꼭지점 'a'와 꼭지점 'b'는 돌출 꼭지점이라고도하는 1 차도를 갖습니다.
격리 된 정점
차수가 0 인 정점을 격리 된 정점이라고합니다.
Example

여기서 정점 'a'와 정점 'b'는 서로 연결되어 있지 않으며 다른 정점에도 연결되어 있지 않습니다. 따라서 'a'와 'b'꼭짓점의 차수는 모두 0입니다. 이들은 분리 된 정점이라고도합니다.
인접
다음은 인접성의 규범입니다-
그래프에서 두 개의 정점은 adjacent, 두 정점 사이에 가장자리가있는 경우. 여기서 정점의 인접성은 두 정점을 연결하는 단일 가장자리에 의해 유지됩니다.
그래프에서 두 모서리 사이에 공통 정점이있는 경우 두 모서리는 인접하다고합니다. 여기서 가장자리의 인접성은 두 가장자리를 연결하는 단일 정점에 의해 유지됩니다.
Example 1
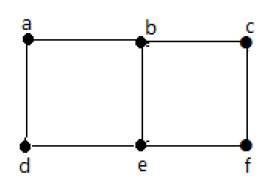
위의 그래프에서-
'a'와 'b'는 인접한 정점입니다. 그 사이에 공통 모서리 'ab'이 있기 때문입니다.
'a'와 'd'는 인접한 정점입니다. 그 사이에 공통 가장자리 'ad'가 있기 때문입니다.
ab '와'be '는 그 사이에 공통 꼭지점'b '가 있기 때문에 인접한 가장자리입니다.
be '와'de '는 인접한 모서리입니다. 그 사이에 공통 정점'e '가 있기 때문입니다.
Example 2
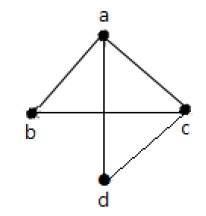
위의 그래프에서-
'a'와 'd'는 인접한 정점입니다. 그 사이에 공통 가장자리 'ad'가 있기 때문입니다.
'c'와 'b'는 인접 정점입니다. 그 사이에 공통 가장자리 'cb'가 있기 때문입니다.
'ad'와 'cd'는 그 사이에 공통 정점 'd'가 있기 때문에 인접한 가장자리입니다.
'ac'와 'cd'는 그 사이에 공통 정점 'c'가 있기 때문에 인접한 가장자리입니다.
평행 모서리
그래프에서 한 쌍의 꼭지점이 둘 이상의 가장자리로 연결된 경우 이러한 가장자리를 평행 가장자리라고합니다.
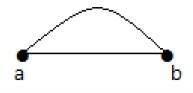
위의 그래프에서 'a'와 'b'는 두 개의 가장자리 'ab'와 'ab'사이에 연결된 두 개의 꼭지점입니다. 따라서 평행 모서리라고합니다.
다중 그래프
평행 한 모서리가있는 그래프를 다중 그래프라고합니다.
Example 1

위의 그래프에는 'ab', 'ac', 'cd', 'cd', 'bd'의 5 개의 간선이 있습니다. 'c'와 'd'사이에 두 개의 평행 한 모서리가 있으므로 다중 그래프입니다.
Example 2
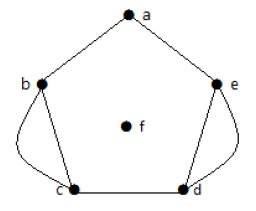
위 그래프에서 꼭지점 'b'와 'c'에는 두 개의 모서리가 있습니다. 꼭지점 'e'와 'd'도 그들 사이에 두 개의 가장자리가 있습니다. 따라서 그것은 Multigraph입니다.
그래프의 차수 시퀀스
그래프에있는 모든 정점의 각도가 내림차순 또는 오름차순으로 배열 된 경우 얻은 시퀀스를 그래프의 각도 시퀀스라고합니다.
Example 1

| 꼭지점 | ㅏ | 비 | 씨 | 디 | 이자형 |
|---|---|---|---|---|---|
| 에 연결 | 기원전 | 기원 후 | 기원 후 | c, b, e | 디 |
| 정도 | 2 | 2 | 2 | 삼 | 1 |
위 그래프에서 꼭짓점 {d, a, b, c, e}에 대해 차수 시퀀스는 {3, 2, 2, 2, 1}입니다.
Example 2

| 꼭지점 | ㅏ | 비 | 씨 | 디 | 이자형 | 에프 |
|---|---|---|---|---|---|---|
| 에 연결 | 있다 | a, c | b, d | c, e | 기원 후 | - |
| 정도 | 2 | 2 | 2 | 2 | 2 | 0 |
위 그래프에서 정점 {a, b, c, d, e, f}의 경우 차수 시퀀스는 {2, 2, 2, 2, 2, 0}입니다.
그래프에는 구조에 따라 그래프의 특성화에 사용되는 다양한 속성이 있습니다. 이러한 속성은 그래프 이론의 영역과 관련된 특정 용어로 정의됩니다. 이 장에서는 모든 그래프에서 공통되는 몇 가지 기본 속성에 대해 설명합니다.
두 정점 사이의 거리
정점 U와 정점 V 사이의 최단 경로에있는 가장자리 수입니다. 두 정점을 연결하는 경로가 여러 개인 경우 가장 짧은 경로가 두 정점 사이의 거리로 간주됩니다.
표기법 − d (U, V)
한 정점에서 다른 정점으로의 경로는 얼마든지있을 수 있습니다. 그중 가장 짧은 것을 선택하면됩니다.
Example
다음 그래프를보세요-

여기서, 꼭지점 'd'에서 꼭지점 'e'또는 단순히 'de'까지의 거리는 그들 사이에 하나의 가장자리가 있기 때문에 1입니다. 꼭지점 'd'에서 꼭지점 'e'로가는 경로는 많습니다.
- da, ab, be
- df, fg, ge
- de (정점 사이의 거리로 간주 됨)
- df, fc, ca, ab, be
- da, ac, cf, fg, ge
꼭지점의 편심
정점에서 다른 모든 정점까지의 최대 거리는 정점의 편심으로 간주됩니다.
표기법 − e (V)
그래프의 특정 정점에서 다른 모든 정점까지의 거리가 취해지며이 거리 중에서 편심이 가장 높은 거리입니다.
Example
위의 그래프에서 'a'의 이심률은 3입니다.
'a'에서 'b'까지의 거리는 1 ( 'ab')입니다.
'a'에서 'c'는 1 ( 'ac')입니다.
'a'에서 'd'는 1 ( 'ad')입니다.
'a'에서 'e'는 2 ( 'ab'- 'be') 또는 ( 'ad'- 'de')입니다.
'a'에서 'f'는 2 ( 'ac'- 'cf') 또는 ( 'ad'- 'df')입니다.
'a'에서 'g'는 3 ( 'ac'- 'cf'- 'fg') 또는 ( 'ad'- 'df'- 'fg')입니다.
따라서 이심률은 3으로, 최대 인 'ag'사이의 거리에서 정점 'a'에서 최대 값입니다.
다시 말해,
e (b) = 3
e (c) = 3
e (d) = 2
e (e) = 3
e (f) = 3
예 (g) = 3
연결된 그래프의 반경
모든 정점의 최소 편심은 그래프 G의 반경으로 간주됩니다. 정점과 다른 모든 정점 사이의 모든 최대 거리 중 최소값은 그래프 G의 반경으로 간주됩니다.
표기법 − r (G)
그래프의 모든 정점 편심에서 연결된 그래프의 반경은 모든 편심 중 최소값입니다.
Example
위 그래프에서 r (G) = 2는 'd'의 최소 편심입니다.
그래프 지름
모든 정점의 최대 편심은 Graph G의 직경으로 간주됩니다. 정점과 다른 모든 정점 사이의 모든 거리 중 최대 값은 Graph G의 직경으로 간주됩니다.
Notation − d(G) − 그래프에서 정점의 모든 편심에서 연결된 그래프의 직경은 모든 편심의 최대 값입니다.
Example
위의 그래프에서 d (G) = 3; 이것은 최대 편심입니다.
센트럴 포인트
그래프의 이심률이 반경과 같으면 그래프의 중심점이라고합니다. 만약
e (V) = r (V),
'V'는 그래프 'G'의 중심점입니다.
Example
예제 그래프에서 'd'는 그래프의 중심점입니다.
e (d) = r (d) = 2
센터
'G'의 모든 중심점 집합을 그래프의 중심이라고합니다.
Example
예제 그래프에서 { 'd'}는 그래프의 중심입니다.
둘레
그만큼 number of edges in the longest cycle of ‘G’ 'G'의 둘레라고합니다.
Example
예제 그래프에서 원주는 6이며, 가장 긴주기 인 acfgeba 또는 acfdeba에서 파생되었습니다.
테두리
'G'의 가장 짧은주기의 모서리 수를 Girth라고합니다.
Notation: g (G).
Example − 예제 그래프에서 그래프의 둘레는 4이며, 가장 짧은주기 acfda 또는 dfged 또는 abeda에서 파생되었습니다.
정점 차수의 합 정리
G = (V, E) 정점이 V = {V 1 , V 2 ,… V n } 인 무 방향 그래프 이면
Corollary 1
G = (V, E) 정점이 V = {V 1 , V 2 ,… V n } 인 유 방향 그래프 이면
Corollary 2
방향이없는 그래프에서 홀수 차수가있는 정점의 수는 짝수입니다.
Corollary 3
무 방향 그래프에서 각 꼭지점의 차수가 k이면
Corollary 4
무 방향 그래프에서 각 꼭지점의 차수가 k 이상이면
| Corollary 5
무 방향 그래프에서 각 꼭지점의 차수가 최대 k이면
정점 수, 모서리 수, 상호 연결성 및 전체 구조에 따라 다양한 유형의 그래프가 있습니다. 이 장에서는 몇 가지 중요한 그래프 유형에 대해서만 설명합니다.
널 그래프
A graph having no edges Null 그래프라고합니다.
예

위의 그래프에는 'a', 'b', 'c'라는 세 개의 꼭지점이 있지만 그 사이에 가장자리가 없습니다. 따라서 그것은 Null 그래프입니다.
사소한 그래프
ㅏ graph with only one vertex Trivial Graph라고합니다.
예

위에 표시된 그래프에는 다른 모서리가없는 꼭지점 'a'가 하나만 있습니다. 따라서 그것은 사소한 그래프입니다.
무 방향 그래프
무 방향 그래프는 간선을 포함하지만 간선은 방향성이 아닙니다.
예
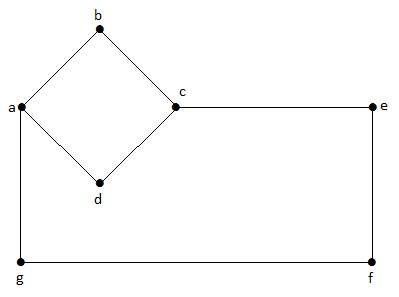
이 그래프에서 'a', 'b', 'c', 'd', 'e', 'f', 'g'는 꼭지점이고 'ab', 'bc', 'cd', 'da ','ag ','gf ','ef '는 그래프의 가장자리입니다. 무 방향 그래프이기 때문에 'ab'와 'ba'간선은 동일합니다. 마찬가지로 다른 모서리도 같은 방식으로 고려됩니다.
유향 그래프
유 방향 그래프에서 각 간선에는 방향이 있습니다.
예

위 그래프에는 7 개의 꼭지점 'a', 'b', 'c', 'd', 'e', 'f', 'g'와 8 개의 모서리 'ab', 'cb', ' dc ','ad ','ec ','fe ','gf '및'ga '. 방향 그래프이기 때문에 각 모서리에는 방향을 나타내는 화살표 표시가 있습니다. 유 방향 그래프에서 'ab'는 'ba'와 다릅니다.
간단한 그래프
그래프 with no loops 그리고 아니 parallel edges 단순 그래프라고합니다.
'n'개의 꼭지점이있는 단일 그래프에서 가능한 최대 간선 수는 n C 2 이며 여기서 n C 2 = n (n – 1) / 2입니다.
'n'꼭지점 = 2 n c 2 = 2 n (n-1) / 2로 가능한 간단한 그래프의 수입니다 .
예
다음 그래프에는 평행 모서리와 루프를 제외하고 최대 값 인 3 개의 모서리가있는 3 개의 꼭지점이 있습니다. 이것은 위의 공식을 사용하여 증명할 수 있습니다.
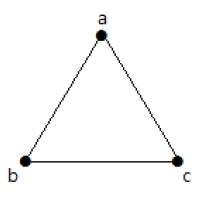
n = 3 꼭지점을 가진 가장자리의 최대 수-
n = 3 꼭짓점을 가진 단순 그래프의 최대 수-
이 8 개의 그래프는 아래와 같습니다.
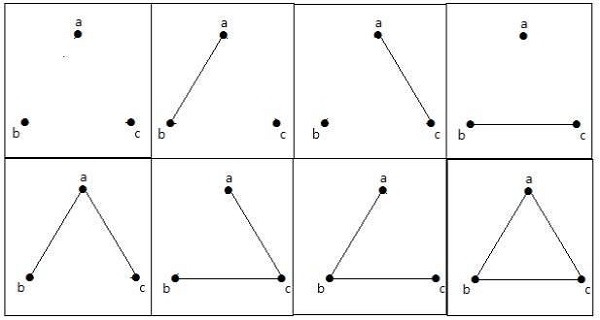
연결된 그래프
그래프 G가 연결되었다고합니다 if there exists a path between every pair of vertices. 그래프의 모든 정점에 대해 최소한 하나의 가장자리가 있어야합니다. 그래서 우리는 그것이 가장자리의 다른쪽에있는 다른 정점에 연결되어 있다고 말할 수 있습니다.
예
다음 그래프에서 각 정점에는 다른 가장자리에 연결된 자체 가장자리가 있습니다. 따라서 연결된 그래프입니다.

연결이 끊긴 그래프
연결된 꼭지점이 두 개 이상 포함되어 있지 않으면 그래프 G는 연결이 끊어집니다.
예 1
다음 그래프는 'a', 'b', 'c', 'd'꼭지점이있는 구성 요소와 'e', 'f', 'g'가있는 구성 요소가있는 두 개의 구성 요소가있는 연결이 끊긴 그래프의 예입니다. 'h'꼭지점.
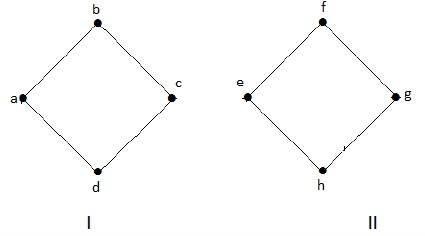
두 구성 요소는 독립적이며 서로 연결되어 있지 않습니다. 따라서 연결이 끊어진 그래프라고합니다.
예 2

이 예에는 서로 연결되지 않은 두 개의 독립 구성 요소 인 abfe와 cd가 있습니다. 따라서 이것은 연결이 끊어진 그래프입니다.
일반 그래프
그래프 G는 규칙적이라고합니다. if all its vertices have the same degree. 그래프에서 각 꼭지점의 차수가 'k'이면 그래프를 'k- 정규 그래프'라고합니다.
예
다음 그래프에서 모든 정점의 차수는 동일합니다. 따라서 이러한 그래프를 일반 그래프라고합니다.
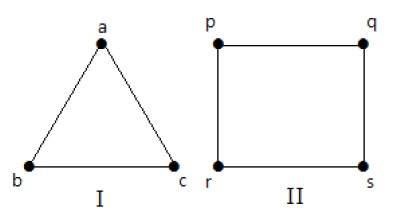
두 그래프 모두에서 모든 정점의 차수는 2입니다.이를 2- 정규 그래프라고합니다.
완전한 그래프
상호 정점이 'n'개있는 간단한 그래프를 완전한 그래프라고하며 denoted by ‘Kn’. 그래프에서a vertex should have edges with all other vertices, 완전한 그래프라고 불렀습니다.
즉, 꼭지점이 그래프의 다른 모든 꼭지점에 연결되어 있으면 완전한 그래프라고합니다.
예
다음 그래프에서 그래프의 각 정점은 그 자체를 제외하고 그래프의 나머지 모든 정점과 연결됩니다.
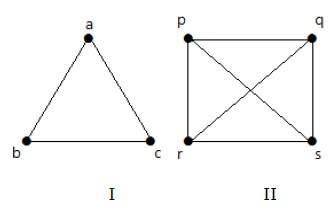
그래프 I에서
| ㅏ | 비 | 씨 | |
|---|---|---|---|
| ㅏ | 연결되지 않은 | 연결됨 | 연결됨 |
| 비 | 연결됨 | 연결되지 않은 | 연결됨 |
| 씨 | 연결됨 | 연결됨 | 연결되지 않은 |
그래프 II에서
| 피 | 큐 | 아르 자형 | 에스 | |
|---|---|---|---|---|
| 피 | 연결되지 않은 | 연결됨 | 연결됨 | 연결됨 |
| 큐 | 연결됨 | 연결되지 않은 | 연결됨 | 연결됨 |
| 아르 자형 | 연결됨 | 연결됨 | 연결되지 않은 | 연결됨 |
| 에스 | 연결됨 | 연결됨 | 연결됨 | 연결되지 않은 |
사이클 그래프
'n'꼭지점 (n> = 3) 및 'n'가장자리가있는 간단한 그래프는 모든 가장자리가 길이 'n'의주기를 형성하는 경우주기 그래프라고합니다.
그래프의 각 꼭지점의 차수가 2 인 경우이를주기 그래프라고합니다.
Notation− C n
예
다음 그래프를 살펴보십시오-
그래프 I에는 'ab-bc-ca'주기를 형성하는 3 개의 모서리가있는 3 개의 꼭지점이 있습니다.
그래프 II에는 'pq-qs-sr-rp'주기를 형성하는 4 개의 모서리가있는 4 개의 꼭지점이 있습니다.
그래프 III에는 'ik-km-ml-lj-ji'주기를 형성하는 5 개의 모서리가있는 5 개의 꼭지점이 있습니다.

따라서 주어진 모든 그래프는 사이클 그래프입니다.
휠 그래프
바퀴 그래프는 새 정점을 추가하여 사이클 그래프 C n-1 에서 얻습니다 . 그 새로운 정점은Hub이것은 C n 의 모든 정점에 연결됩니다 .
표기법-W n
W의 가장자리 수 n = 허브에서 다른 모든 정점까지의 가장자리 수 +
허브가없는 사이클 그래프의 다른 모든 노드의 에지 수입니다.
= (n–1) + (n–1)
= 2 (n–1)
예
다음 그래프를 살펴보십시오. 그들은 모두 바퀴 그래프입니다.
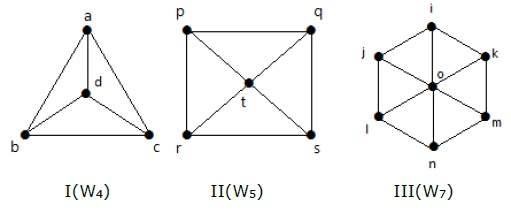
그래프 I에서는 'd'라는 중간에 꼭지점을 추가하여 C 3 에서 얻습니다 . W 4 로 표시됩니다 .
W4의 모서리 수 = 2 (n-1) = 2 (3) = 6
그래프 II에서는 중간에 't'라는 정점을 추가하여 C4에서 구합니다. W 5 로 표시됩니다 .
W5의 모서리 수 = 2 (n-1) = 2 (4) = 8
그래프 III에서는 'o'라는 중간에 꼭지점을 추가하여 C 6 에서 얻습니다 . W 7 로 표시됩니다 .
W4의 모서리 수 = 2 (n-1) = 2 (6) = 12
순환 그래프
그래프 with at least one 주기를 순환 그래프라고합니다.
예
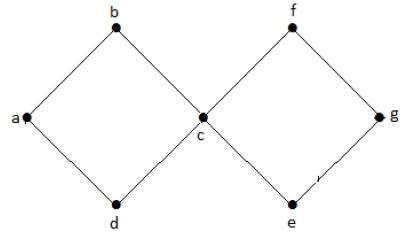
위의 예제 그래프에는 abcda와 cfgec의 두 사이클이 있습니다. 따라서 순환 그래프라고합니다.
비순환 그래프
그래프 with no cycles 비순환 그래프라고합니다.
예
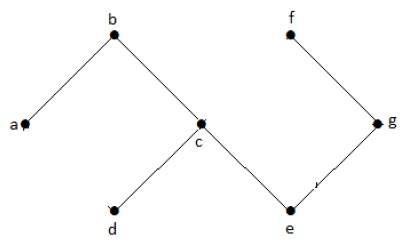
위의 예제 그래프에는 사이클이 없습니다. 따라서 비순환 그래프입니다.
이분 그래프
정점 분할 V = {V 1 , V 2 }가 있는 간단한 그래프 G = (V, E)를 이분 그래프라고합니다.if every edge of E joins a vertex in V1 to a vertex in V2.
일반적으로 Bipertite 그래프에는 V1과 V2의 두 세트의 정점이 있으며, 모서리가 그려지면 세트 V 1의 정점을 V 2 세트의 정점에 연결해야합니다 .
예
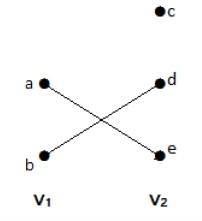
이 그래프에서 두 세트의 정점 V 1 과 V 2를 관찰 할 수 있습니다 . 여기서 'ae'와 'bd'라는 이름의 두 모서리는 두 세트 V 1 및 V 2 의 정점을 연결합니다 .
완전한 이분 그래프
분할이 V = {V 1 , V 2 } 인 이분 그래프 'G', G = (V, E) 는 V 1의 모든 정점이 V 2의 모든 정점에 연결 되면 완전한 이분 그래프라고합니다 .
일반적으로 완전한 이분 그래프는 세트 V 1의 각 정점을 세트 V 2의 각 정점에 연결합니다 .
예
다음 그래프는 세트 V 1의 각 정점을 세트 V 2의 각 정점에 연결하는 간선이 있기 때문에 완전한 이분 그래프 입니다.
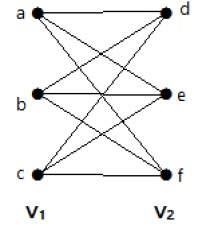
| V 1 | = m 및 | V 2 | = n이면 완전한 이분 그래프는 K m, n으로 표시됩니다 .
- K m, n 에는 (m + n) 꼭지점과 (mn) 가장자리가 있습니다.
- K m, n 은 m = n 인 경우 일반 그래프입니다.
일반적으로 complete bipartite graph is not a complete graph.
m = n = 1 인 경우 K m, n 은 완전한 그래프입니다.
n 개의 정점이있는 이분 그래프의 최대 간선 수는 다음과 같습니다.
[N 2 / 4]
n = 10, k5, 5 = [n2 / 4] = [10 2 / 4] = 25입니다.
마찬가지로 K6, 4 = 24
K7, 3 = 21
K8, 2 = 16
K9, 1 = 9
n = 9이면 k5, 4 = [n2 / 4] = [92/4] = 20
마찬가지로 K6, 3 = 18
K7, 2 = 14
K8, 1 = 8
'G'에 홀수 길이의주기가없는 경우 'G'는 이분 그래프입니다. 이분 그래프의 특별한 경우는 별 그래프입니다.
스타 그래프
K1, n-1 형식의 완전한 이분 그래프는 n- 꼭지점이있는 별 그래프입니다. 단일 정점이 한 세트에 속하고 나머지 모든 정점이 다른 세트에 속하는 경우 스타 그래프는 완전한 이분 그래프입니다.
예
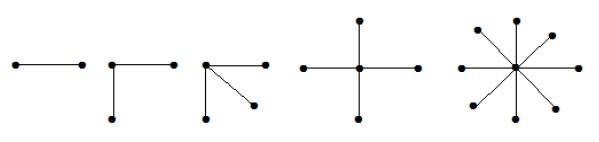
위의 그래프에서 'n'정점 중 모든 'n-1'정점은 단일 정점에 연결됩니다. 따라서 별 그래프 인 K 1 , n-1 의 형태입니다 .
그래프 보완
'G-'는 'G'와 같은 일부 정점이있는 간단한 그래프이고 가장자리가 G에 없으면 가장자리 {U, V}가 'G-'에 있습니다. 즉, 두 정점이 인접 해 있음을 의미합니다. 두 꼭지점이 G에서 인접하지 않은 경우 'G-'에서.
그래프 I에 존재하는 간선이 다른 그래프 II에없고 그래프 I와 그래프 II가 모두 결합되어 완전한 그래프를 형성하는 경우 그래프 I와 그래프 II를 서로 보완이라고합니다.
예
다음 예에서 graph-I에는 두 개의 간선 'cd'와 'bd'가 있습니다. 보완 그래프 II에는 네 개의 간선이 있습니다.
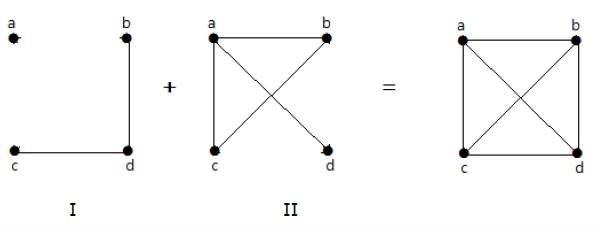
그래프 -I의 간선은 그래프 -II에 존재하지 않으며 그 반대의 경우도 마찬가지입니다. 따라서 두 그래프의 조합은 'n'꼭지점의 완전한 그래프를 제공합니다.
Note − 두 개의 보완적인 그래프의 조합은 완전한 그래프를 제공합니다.
'G'가 간단한 그래프이면
| E (G) | + | E ( 'G-') | = | E (Kn) |, 여기서 n = 그래프의 꼭지점 수.
예
'G'를 9 개의 꼭지점과 12 개의 모서리가있는 간단한 그래프라고 가정하고 'G-'에서 모서리 수를 찾으십시오.
당신은 | E (G) | + | E ( 'G-') | = | E (Kn) |
12 + | E ( 'G-') | =
9 (9-1) / 2 = 9 C 2
12 + | E ( 'G-') | = 36
| E ( 'G-') | = 24
'G'는 40 개의 간선이있는 간단한 그래프이고 그 보수 'G-'에는 38 개의 간선이 있습니다. 그래프 G 또는 'G-'에서 꼭지점 수를 찾으십시오.
그래프의 꼭지점 수를 'n'으로 지정합니다.
| E (G) | + | E ( 'G-') | = | E (Kn) |
40 + 38 = n (n-1) / 2
156 = n (n-1)
13 (12) = n (n-1)
n = 13
트리는 단일 사이클도 포함하지 않는 그래프입니다. 그래픽 형식으로 계층 구조를 나타냅니다. 트리는 가장 단순한 그래프 클래스에 속합니다. 단순함에도 불구하고 구조가 풍부합니다.
트리는 컴퓨터 과학의 데이터 구조에서 트리만큼이나 단순한 패밀리 트리에 이르기까지 다양한 유용한 응용 프로그램을 제공합니다.
나무
ㅏ connected acyclic graph나무라고합니다. 즉,주기가없는 연결된 그래프를 트리라고합니다.
나무의 가장자리는 다음과 같이 알려져 있습니다. branches. 나무의 요소를 노드라고합니다. 자식 노드가없는 노드가 호출됩니다.leaf nodes.
'n'꼭지점이있는 나무에는 'n-1'가장자리가 있습니다. 'n-1'보다 가장자리가 하나 더 추가 된 경우 추가 가장자리는 분명히 두 개의 정점과 쌍을 이루어 하나의주기를 형성해야합니다. 그러면 트리 그래프를 위반하는 순환 그래프가됩니다.
Example 1
여기에 표시된 그래프는주기가없고 연결되어 있기 때문에 트리입니다. 4 개의 정점과 3 개의 가장자리가 있습니다. 즉, 정의에서 언급 한대로 'n'정점의 경우 'n-1'가장자리입니다.
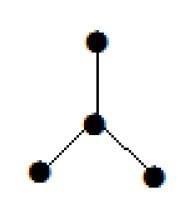
Note -모든 나무에는 차수가 1 인 꼭지점이 2 개 이상 있습니다.
Example 2
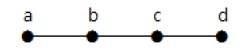
위의 예에서 정점 'a'와 'd'는 차수가 1입니다. 그리고 다른 두 꼭지점 'b'와 'c'는 차수가 2입니다. 이는 사이클을 형성하지 않는 경우 그래프의 어느 곳에 나 최소한 두 개의 단일 에지가 있어야하기 때문에 가능합니다. 정도가 1 인 두 개의 모서리 일뿐입니다.
숲
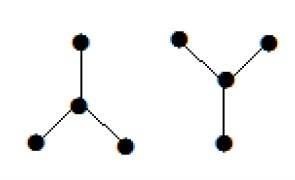
ㅏ disconnected acyclic graph숲이라고합니다. 즉, 분리 된 나무 모음을 숲이라고합니다.
Example
다음 그래프는 두 개의 하위 그래프처럼 보입니다. 그러나 그것은 단절된 단일 그래프입니다. 이 그래프에는주기가 없습니다. 따라서 그것은 분명히 숲입니다.
스패닝 트리
G를 연결된 그래프라고하면 G의 하위 그래프 H는 다음과 같은 경우 G의 스패닝 트리라고합니다.
- H는 나무
- H는 G의 모든 정점을 포함합니다.
무 방향 그래프 G의 스패닝 트리 T는 G의 모든 정점을 포함하는 부분 그래프입니다.
Example

위의 예에서 G는 연결된 그래프이고 H는 G의 하위 그래프입니다.
분명히 그래프 H에는주기가 없으며 총 정점 수보다 하나 적은 6 개의 모서리가있는 트리입니다. 따라서 H는 G의 스패닝 트리입니다.
회로 순위
'G'를 'n'꼭지점과 'm'간선이있는 연결된 그래프라고합시다. G의 스패닝 트리 'T'에는 (n-1) 개의 가장자리가 있습니다.
따라서 스패닝 트리 = m- (n-1)을 얻기 위해 'G'에서 삭제해야하는 에지의 수를 G의 회로 순위라고합니다.
스패닝 트리에서는 'n-1'모서리가 필요하기 때문에이 공식은 사실입니다. 'm'간선 중에는 그래프에서 'n-1'간선을 유지해야합니다.
따라서 'm'에서 'n–1'간선을 삭제하면 순환을 형성해서는 안되는 스패닝 트리를 얻기 위해 그래프에서 간선이 제거됩니다.
Example
다음 그래프를보세요-
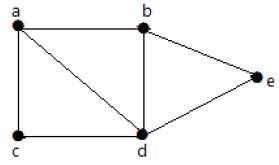
위의 예에 제공된 그래프의 경우 m = 7 개의 모서리와 n = 5 개의 꼭지점이 있습니다.
그런 다음 회로 순위는-
Example
'G'를 6 개의 정점이있는 연결된 그래프이고 각 정점의 차수가 3이라고합시다. 'G'의 회로 순위를 찾으십시오.
정점 정리의 합에 의해,
Kirchoff의 정리
Kirchoff의 정리는 연결된 그래프에서 형성 될 수있는 스패닝 트리의 수를 찾는 데 유용합니다.
Example
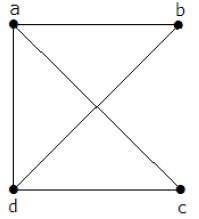
행렬 'A'는 두 꼭지점 사이에 가장자리가 있으면 '1', 그렇지 않으면 '0'으로 지정되어야합니다.
$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$kirchoff의 정리를 사용하여 주요 대각선 값을 꼭지점의 각도로 대체하고 다른 모든 요소를 -1로 바꾸도록 변경해야합니다.
$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$따라서 스패닝 트리 수 = 8입니다.
한 정점에서 다른 정점으로 그래프를 횡단 할 수 있는지 여부는 그래프가 연결된 방식에 따라 결정됩니다. 연결성은 그래프 이론의 기본 개념입니다. 연결성은 그래프가 연결되었는지 연결 해제되었는지를 정의합니다. 가장자리 연결 및 정점 연결로 알려진 가장자리 및 정점을 기반으로하는 하위 주제가 있습니다. 자세히 논의하겠습니다.
연결성
그래프는 connected if there is a path between every pair of vertex. 모든 정점에서 다른 정점으로 이동할 경로가 있어야합니다. 이를 그래프의 연결이라고합니다. 여러 개의 연결이 끊긴 꼭지점과 가장자리가있는 그래프는 연결이 끊겼다 고합니다.
Example 1
다음 그래프에서 한 정점에서 다른 정점으로 이동할 수 있습니다. 예를 들어 'ab-e'경로를 사용하여 'a'꼭지점에서 'e'꼭지점으로 이동할 수 있습니다.
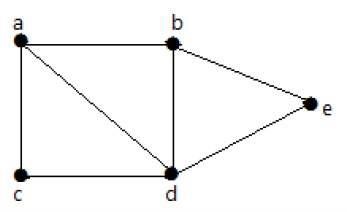
Example 2
다음 예에서는 정점 'a'에서 정점 'f'로 이동하는 것이 불가능합니다. 그 사이에는 직접 또는 간접적으로 경로가 없기 때문입니다. 따라서 연결이 끊어진 그래프입니다.
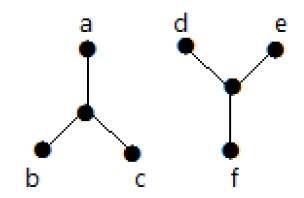
정점 잘라 내기
'G'를 연결된 그래프라고합시다. 꼭지점 V ∈ G는 'G'( 'G'에서 'V'삭제) 결과 그래프가 끊어지면 'G'의 절단 꼭지점이라고합니다. 그래프에서 절단 된 정점을 제거하면 두 개 이상의 그래프로 분할됩니다.
Note − 절단 된 정점을 제거하면 그래프가 연결 해제 될 수 있습니다.
연결된 그래프 'G'에는 최대 (n–2) 개의 절단 꼭지점이있을 수 있습니다.
Example
다음 그래프에서 꼭지점 'e'와 'c'는 잘린 꼭지점입니다.

'e'또는 'c'를 제거하면 그래프가 연결이 끊어진 그래프가됩니다.

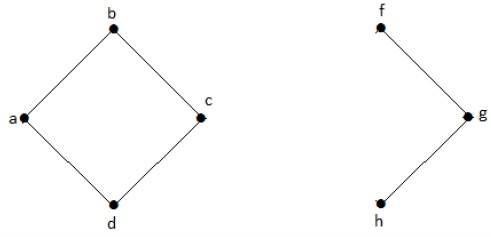
'g'가 없으면 꼭지점 'c'와 꼭지점 'h'사이에 경로가 없습니다. 따라서 잘라낸 꼭지점이 'e'인 연결 해제 된 그래프입니다. 마찬가지로 'c'는 위 그래프의 절단 꼭지점이기도합니다.
절단면 (브리지)
'G'를 연결된 그래프라고합시다. 에지 'e'∈ G는 'G-e'가 그래프 연결이 끊어진 경우 절단 에지라고합니다.
그래프에서 모서리를 제거하면 두 개 이상의 그래프가 생성되는 경우 해당 모서리를 절단 모서리라고합니다.
Example
다음 그래프에서 절단 모서리는 [(c, e)]입니다.

그래프에서 모서리 (c, e)를 제거하면 연결이 끊어진 그래프가됩니다.


위의 그래프에서 모서리 (c, e)를 제거하면 그래프가 두 개로 나뉩니다. 따라서 모서리 (c, e)는 그래프의 절단 모서리입니다.
Note − 'G'를 'n'개의 정점이있는 연결된 그래프라고 가정하고
절단 모서리 e ∈ G 모서리 'e'가 G의 어떤주기에도 속하지 않는 경우에만.
가능한 절단 모서리의 최대 수는 'n-1'입니다.
절단 모서리가 존재할 때마다 절단 모서리의 하나 이상의 정점이 절단 정점이므로 절단 정점도 존재합니다.
절단 정점이있는 경우 절단 모서리가있을 수도 있고 없을 수도 있습니다.
그래프의 컷 세트
'G'= (V, E)를 연결된 그래프라고합시다. G에서 E '의 모든 모서리를 삭제하면 G가 연결 해제되면 E의 부분 집합 E'를 G의 컷 세트라고합니다.
그래프에서 특정 수의 간선을 삭제하여 연결이 끊어지면 삭제 된 간선을 그래프의 절단 세트라고합니다.
Example
다음 그래프를 살펴보십시오. 컷 세트는 E1 = {e1, e3, e5, e8}입니다.
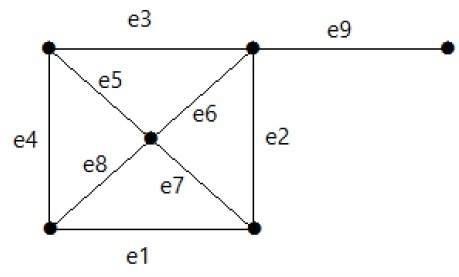
그래프에서 절단 세트 E1을 제거하면 다음과 같이 나타납니다.
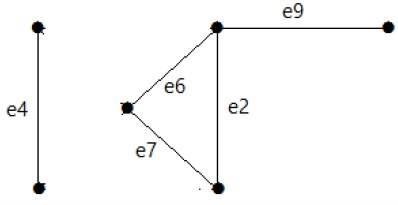
마찬가지로, 그래프를 분리 할 수있는 다른 컷 세트가 있습니다.
E3 = {e9} – 그래프의 가장 작은 절단 세트.
E4 = {e3, e4, e5}
에지 연결
'G'를 연결된 그래프라고합시다. 제거로 인해 'G'가 연결 해제되는 최소 에지 수를 G의 에지 연결이라고합니다.
Notation − λ (G)
즉, number of edges in a smallest cut set of G G의 에지 연결이라고합니다.
'G'에 절단 모서리가있는 경우 λ (G)는 1입니다 (G의 모서리 연결).
Example
다음 그래프를 살펴보십시오. 두 개의 최소 간선을 제거하면 연결된 그래프의 연결이 끊어집니다. 따라서 에지 연결 (λ (G))은 2입니다.
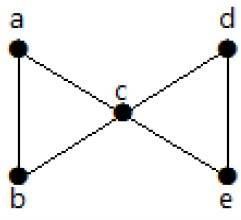
다음은 두 모서리를 제거하여 그래프를 분리하는 네 가지 방법입니다.

정점 연결
'G'를 연결된 그래프라고합시다. 제거가 'G'를 연결 해제하거나 'G'를 사소한 그래프로 줄이는 최소 정점 수를 정점 연결이라고합니다.
Notation − K (G)
Example
위 그래프에서 'e'와 'i'꼭짓점을 제거하면 그래프가 연결 해제됩니다.

G에 절단 정점이 있으면 K (G) = 1입니다.
Notation − 연결된 그래프 G에 대해
K (G) ≤ λ (G) ≤ δ (G)
정점 연결 (K (G)), 가장자리 연결 (λ (G)), 최소 G (δ (G)) 각도.
Example
다음 그래프에 대해 λ (G)와 K (G)를 계산하십시오-
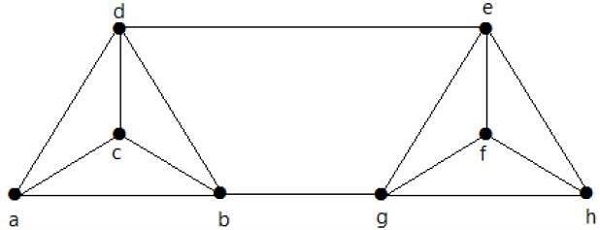
Solution
그래프에서
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
가장자리 {d, e} 및 {b, h}를 삭제하면 G 연결을 끊을 수 있습니다.
따라서,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
(2) 및 (3)에서 정점 연결 K (G) = 2
커버링 그래프는 다른 그래프에 해당하는 모든 정점 또는 모든 모서리를 포함하는 하위 그래프입니다. 모든 정점을 포함하는 하위 그래프를line/edge covering. 모든 모서리를 포함하는 하위 그래프를vertex covering.
라인 커버링
G = (V, E)를 그래프라고합시다. G의 모든 꼭지점이 C에서 적어도 하나의 가장자리에 입사하는 경우 부분 집합 C (E)를 G의 선 커버라고합니다. 즉,
deg (V) ≥ 1 ∀ V ∈ G
각 꼭지점이 가장자리로 다른 꼭지점과 연결되어 있기 때문입니다. 따라서 최소 차수가 1입니다.
Example
다음 그래프를보세요-
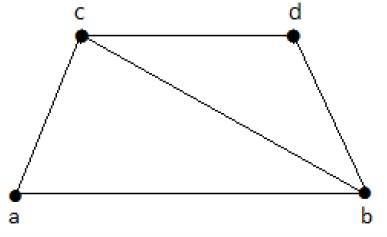
라인 커버링이있는 하위 그래프는 다음과 같습니다.
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
'G'의 선 커버링은 'G'에 고립 된 꼭지점이있는 경우에만 존재하지 않습니다. 'n'꼭지점이있는 그래프의 선 커버링에는 최소한 [n / 2] 개의 가장자리가 있습니다.
최소 라인 커버링
그래프 G의 C를 덮는 선은 최소라고합니다. if no edge can be deleted from C.
Example
위 그래프에서 선을 덮은 부분 그래프는 다음과 같습니다.
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
여기서 C 1 , C 2 , C 3 은 최소한의 라인 커버링이지만 C 4 는 {b, c}를 삭제할 수 있기 때문이 아닙니다.
최소 라인 커버링
그것은 또한 알려져 있습니다 Smallest Minimal Line Covering. 최소한의 가장자리로 덮는 최소 선을 'G'의 최소 선 덮기라고합니다. 'G'를 덮는 최소 선의 가장자리 수를line covering number'G'(α 1 ).
Example
위의 예에서 C 1 및 C 2 는 G 및 α 1 = 2 의 최소 선 커버링입니다 .
모든 라인 커버에는 최소한의 라인 커버가 포함됩니다.
모든 라인 커버링에는 최소 라인 커버링 이 포함되지 않습니다 (C 3 에는 최소 라인 커버링이 포함되지 않습니다.
최소한의 라인 커버링에는 사이클이 포함되어 있지 않습니다.
'C'를 덮는 선에 길이 3 이상의 경로가 포함되어 있지 않으면 'C'의 모든 구성 요소가 별 그래프이고 별 그래프에서 가장자리를 삭제할 수 없기 때문에 'C'는 최소한의 선 덮개입니다.
정점 덮음
'G'= (V, E)를 그래프라고합시다. 'G'의 모든 모서리가 'K'의 꼭지점에 입사하거나 포함되는 경우 V의 부분 집합 K를 'G'의 꼭지점 덮음이라고합니다.
Example
다음 그래프를보세요-
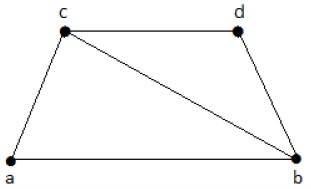
위의 그래프에서 파생 될 수있는 하위 그래프는 다음과 같습니다.
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}
여기서 K 1 , K 2 , K 3 은 꼭지점을 덮는 반면 K 4 는 가장자리 {bc}를 덮지 않기 때문에 꼭지점을 덮지 않습니다.
최소 정점 커버링
그래프 'G'의 정점 'K'는 'K'에서 정점을 삭제할 수없는 경우 최소한의 정점을 덮는다 고합니다.
Example
위 그래프에서 꼭짓점을 덮는 부분 그래프는 다음과 같습니다.
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
여기서 K 1 과 K 2 는 최소한의 정점 커버링이지만 K 3 에서는 정점 'd'를 삭제할 수 있습니다.
최소 정점 커버링
가장 작은 최소 정점 덮음이라고도합니다. 최소 꼭지점 수를 갖는 그래프 'G'의 최소 꼭지점 커버링을 최소 꼭지점 커버링이라고합니다.
'G'의 최소 꼭지점을 덮는 꼭지점의 개수를 G의 꼭지점 개수 (α 2 )라고합니다.
Example
다음 그래프에서 꼭짓점을 덮는 부분 그래프는 다음과 같습니다.
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}

여기서 K 1 은 꼭지점이 두 개뿐이므로 G의 최소 꼭지점 커버입니다. α 2 = 2.
일치하는 그래프는 서로 인접한 가장자리가없는 그래프의 하위 그래프입니다. 간단히 말해서 두 모서리 사이에 공통 정점이 없어야합니다.
어울리는
'G'= (V, E)를 그래프라고합시다. 서브 그래프는 매칭 M (G)이라고합니다.if each vertex of G is incident with at most one edge in M즉,
deg (V) ≤ 1 ∀ V ∈ G
즉, 일치하는 그래프 M (G)에서 정점의 차수는 1 또는 0이어야하며, 여기서 가장자리는 그래프 G에서 입사해야합니다.
Notation − M (G)
Example
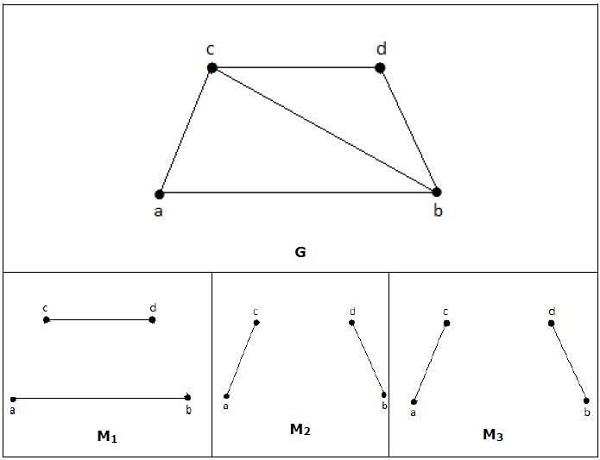

매칭에서
deg (V) = 1이면 (V)가 일치한다고합니다.
deg (V) = 0이면 (V)는 일치하지 않습니다.
일치에서 두 모서리가 인접하지 않습니다. 두 모서리가 인접하면 두 모서리를 연결하는 정점의 정도가 일치 규칙을 위반하는 정도가 2이기 때문입니다.
최대 매칭
그래프 'G'의 일치하는 M은 최대라고합니다. if no other edges of ‘G’ can be added to M.
Example

위 그래프에서 M1, M2, M3은 G의 최대 매칭입니다.
최대 매칭
최대 최대 일치라고도합니다. 최대 일치는 최대 모서리 수와의 최대 일치로 정의됩니다.
'G'의 최대 일치에있는 모서리 수를 matching number.
Example
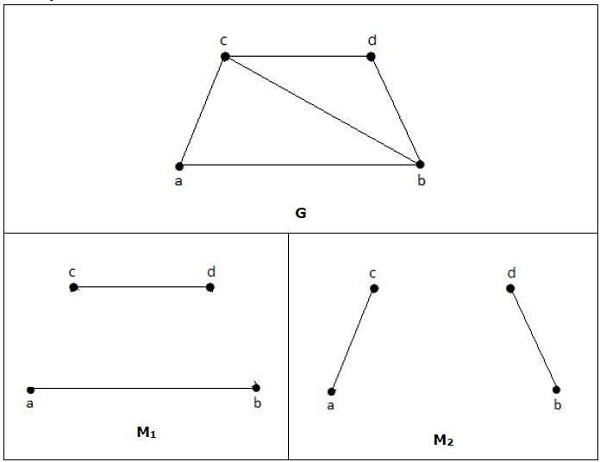
위의 예에서 주어진 그래프의 경우 M1과 M2는 'G'의 최대 일치 값이고 일치 수는 2입니다. 따라서 그래프 G를 사용하면 최대 2 개의 모서리 만있는 부분 그래프 만 형성 할 수 있습니다. 따라서 우리는 일치하는 숫자가 2입니다.
완벽한 매칭
그래프 (G)의 일치 (M)는 그래프 g (G)의 모든 정점이 일치 (M)의 정확히 하나의 모서리에 입사하는 경우 완벽하게 일치한다고합니다.
deg (V) = 1∀V
하위 그래프의 각 꼭지점의 차수는 1이어야합니다.
Example
다음 그래프에서 M1과 M2는 G의 완벽한 매칭의 예입니다.
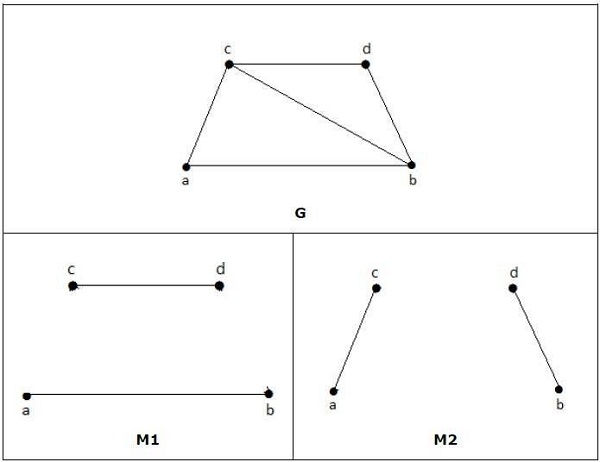
Note − 완벽하게 일치하는 그래프에 에지를 하나 더 추가 할 기회가 없기 때문에 그래프의 모든 완전 일치는 그래프의 최대 일치입니다.
그래프의 최대 일치가 완벽 할 필요는 없습니다. 그래프 'G'가 완벽하게 일치하면 정점 수 | V (G) | 짝수이다. 홀수이면 마지막 정점이 다른 정점과 쌍을 이루고 마지막으로 차수가 0 인 다른 정점과 쌍을 이룰 수없는 단일 정점이 남습니다. 완벽한 매칭 원칙을 분명히 위반합니다.
Example
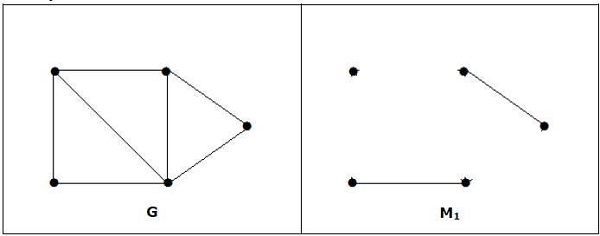
Note− 위 진술의 반대가 사실 일 필요는 없습니다. G에 정점이 짝수이면 M1이 완벽 할 필요는 없습니다.
Example
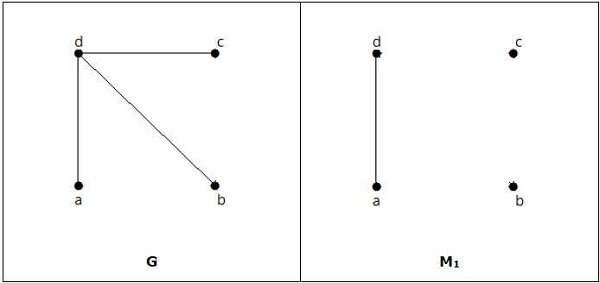
일치하지만 꼭지점이 짝수 인 경우에도 완벽한 일치는 아닙니다.
독립 세트는 세트로 표시됩니다.
없어야한다 any edges adjacent to each other. 두 모서리 사이에 공통 정점이 없어야합니다.
없어야한다 any vertices adjacent to each other. 두 정점 사이에 공통 가장자리가 없어야합니다.
독립 라인 세트
'G'= (V, E)를 그래프라고합시다. L의 두 모서리가 인접하지 않은 경우 E의 하위 집합 L을 'G'의 독립 선 집합이라고합니다. 이러한 세트를 독립 라인 세트라고합니다.
Example
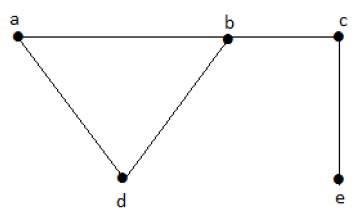
다음 하위 집합을 고려해 보겠습니다.
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.
Maximal Independent Line Set
An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.
Example
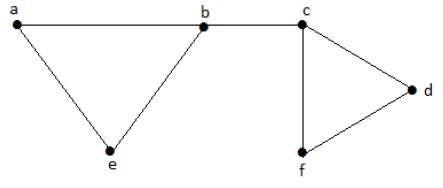
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L2 and L3 are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.
Maximum Independent Line Set
A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
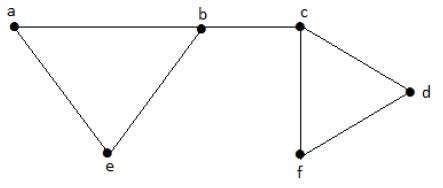
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L3 is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.
Note − For any graph G with no isolated vertex,
α1 + β1 = number of vertices in a graph = |V|
Example
Line covering number of Kn/Cn/wn,
$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$Line independent number (Matching number) = β1 = [n/2] α1 + β1 = n.
Independent Vertex Set
Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.
Example

Consider the following subsets from the above graphs −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Clearly S1 is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S2, S3, and S4 are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.
최대 독립 정점 세트
'G'를 그래프라고하면 'G'의 다른 정점을 'S'에 추가 할 수없는 경우 'G'의 독립 정점 집합이 최대라고합니다.
Example
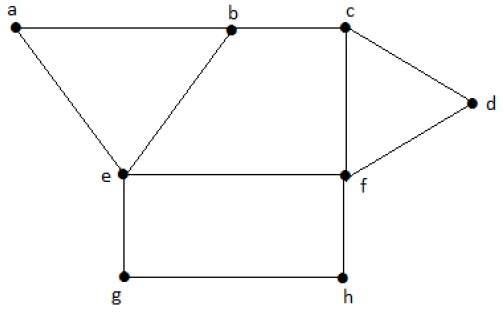
위 그래프에서 다음 하위 집합을 고려하십시오.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 2 및 S 3 은 'G'의 최대 독립 정점 세트입니다. S 1 과 S 4 에서 다른 정점을 추가 할 수 있습니다. 그러나 S 2 와 S 3 에서는 다른 정점을 추가 할 수 없습니다.
최대 독립 정점 세트
최대 정점 수를 가진 'G'의 최대 독립 정점 세트를 최대 독립 정점 세트라고합니다.
Example

위의 그래프에서 다음 하위 집합을 고려하십시오.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 3 만이 가장 많은 수의 정점을 포함하므로 최대 독립 정점 세트입니다. 'G'의 최대 독립 정점 집합에있는 정점의 수를 G의 독립 정점 수 (β 2 )라고합니다.
Example
전체 그래프 K n ,
정점 덮음 수 = α 2 = n−1
정점 독립 수 = β 2 = 1
α 2 + β 2 = n이 있습니다.
완전한 그래프에서 각 정점은 나머지 (n-1) 정점에 인접 해 있습니다. 따라서 K n 의 최대 독립 세트 에는 꼭지점이 하나만 포함됩니다.
따라서 β 2 = 1
및 α 2 = | v | − β 2 = n-1
Note − 모든 그래프 'G'= (V, E)
- α 2 + β 2 = | v |
- 'S'가 'G'의 독립적 인 정점 집합 인 경우 (V – S)는 G의 정점 커버입니다.
그래프 색상 지정은 일부 제약 조건 하에서 꼭지점, 가장자리 및 영역과 같은 그래프 구성 요소에 레이블을 지정하는 간단한 방법 일뿐입니다. 그래프에서 두 개의 인접한 정점, 인접한 가장자리 또는 인접한 영역은 최소 색상 수로 색상이 지정되지 않습니다. 이 번호는chromatic number 그래프는 properly colored graph.
그래프 색상을 지정하는 동안 그래프에 설정된 제약은 색상, 색상 순서, 색상 할당 방법 등입니다. 색상은 꼭지점이나 특정 영역에 부여됩니다. 따라서 동일한 색상을 갖는 정점 또는 영역은 독립적 인 세트를 형성합니다.
정점 채색
정점 색상은 인접한 두 정점이 같은 색을 가지지 않도록 그래프 'G'의 정점에 색상을 할당하는 것입니다. 간단히 말해서, 가장자리의 두 정점이 같은 색이어서는 안됩니다.
색채 번호
그래프 'G'의 꼭지점 채색에 필요한 최소 색상 수를 G의 색수라고하며 X (G)로 표시됩니다.
'G'가 널 그래프 인 경우에만 χ (G) = 1입니다. 'G'가 널 그래프가 아니면 χ (G) ≥ 2입니다.
Example
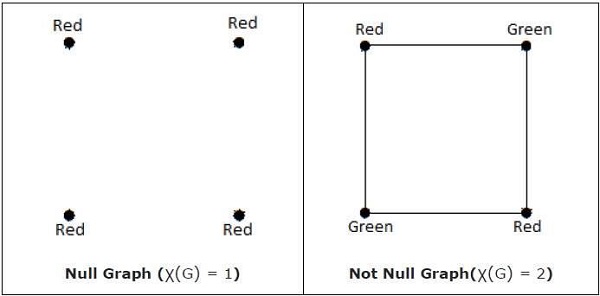
Note − 그래프 'G'는 최대 n 개의 색상, 즉 X (G) ≤ n을 사용하는 정점 색상이있는 경우 n-coverable이라고합니다.
지역 색상
영역 색상 지정은 두 개의 인접한 영역이 동일한 색상을 갖지 않도록 평면 그래프의 영역에 색상을 할당하는 것입니다. 공통 모서리가있는 경우 두 영역이 인접 해 있다고합니다.
Example
다음 그래프를 살펴보십시오. 영역 'aeb'와 'befc'는 두 영역 사이에 공통 가장자리 'be'가 있기 때문에 인접합니다.
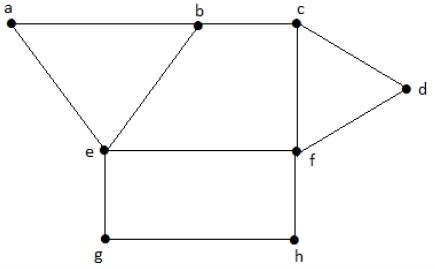
마찬가지로 다른 영역도 인접성을 기준으로 색상이 지정됩니다. 이 그래프는 다음과 같이 색상이 지정됩니다.
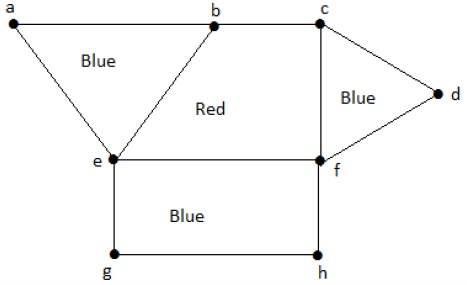
Example
Kn의 색수는
- n
- n–1
- [n/2]
- [n/2]
K 4 로이 예를 고려하십시오 .

전체 그래프에서 각 정점은 나머지 (n – 1) 정점에 인접 해 있습니다. 따라서 각 정점에는 새로운 색상이 필요합니다. 따라서 K의 색 수가 N = N.
그래프 채색의 응용
그래프 색상은 그래프 이론에서 가장 중요한 개념 중 하나입니다. 그것은 같은 컴퓨터 과학의 많은 실시간 응용 프로그램에서 사용됩니다-
- Clustering
- 데이터 수집
- 이미지 캡처
- 이미지 분할
- Networking
- 자원 할당
- 프로세스 스케줄링
그래프는 동일한 수의 꼭지점, 가장자리 및 동일한 가장자리 연결을 갖는 다른 형태로 존재할 수 있습니다. 이러한 그래프를 동형 그래프라고합니다. 이 장에서는 주로 그래프를 참조하고 서로 인식 할 목적으로 그래프에 레이블을 지정합니다.
동형 그래프
두 그래프 G 1 및 G 2 는 다음과 같은 경우 동형이라고합니다.
구성 요소 (정점 및 모서리)의 수는 동일합니다.
에지 연결이 유지됩니다.
Note-간단히 말해서, 두 개의 동형 그래프 중 하나는 다른 하나의 수정 된 버전입니다. 레이블이없는 그래프도 동형 그래프로 생각할 수 있습니다.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
G 1 ≡ G 2 다음-
| V (G 1 ) | = | V (G 2 ) |
| E (G 1 ) | = | E (G 2 ) |
G 1 과 G 2 의 차수 시퀀스 는 동일합니다.
정점 {V 1 , V 2 , .. Vk}가 G 1 에서 길이 K의주기를 형성 하면 정점 {f (V 1 ), f (V 2 ),… f (Vk)}가주기를 형성해야합니다. 길이 K in G 2 .
위의 모든 조건은 그래프 G 1 및 G 2 가 동형이 되려면 필요하지만 그래프가 동형임을 증명하는 데 충분하지 않습니다.
(G 1 ≡ G 2 ) (G 1 − ≡ G 2 −) 여기서 G 1 과 G 2 가 단순한 그래프 인 경우에만 .
(G 1 ≡ G 2 ) G 1 과 G 2 의 인접 행렬 이 같은 경우.
(G 1 ≡ G 2 ) G의 대응하는 서브 그래프 만하고 있으면 1 및 G 2 (G1 일부 정점 그래프 G에서의 이미지 삭제함으로써 얻어지는 2 ) 동형이다.
Example
다음 중 동형 그래프는 무엇입니까?
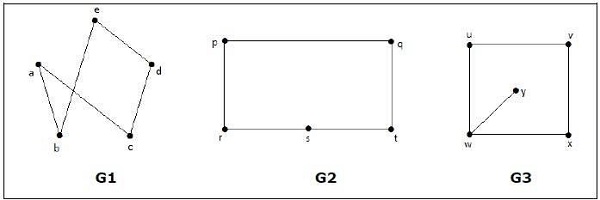
그래프 G 3 에서 정점 'w'는 차수가 3 뿐인 반면 다른 모든 그래프 정점은 차수가 2입니다. 따라서 G3은 G 1 또는 G 2 와 동형이 아닙니다 .
G 1 과 G 2 를 보완 하면-
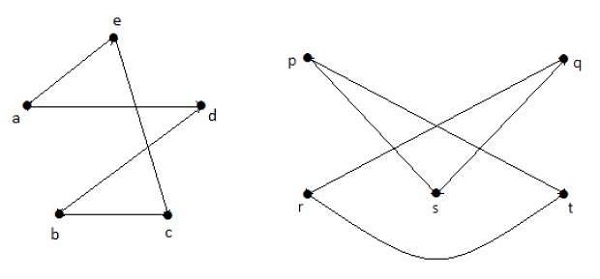
여기에서 (G 1 -≡ G 2- ), 따라서 (G 1 ≡ G 2 ).
평면 그래프
그래프 'G'는 두 모서리가 정점이 아닌 점에서 서로 교차하지 않도록 평면이나 구에 그릴 수있는 경우 평면이라고합니다.
Example
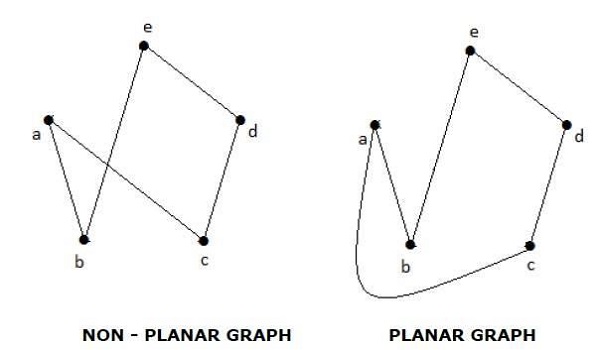
지역
모든 평면형 그래프는 평면을 영역이라고하는 연결된 영역으로 나눕니다.
Example
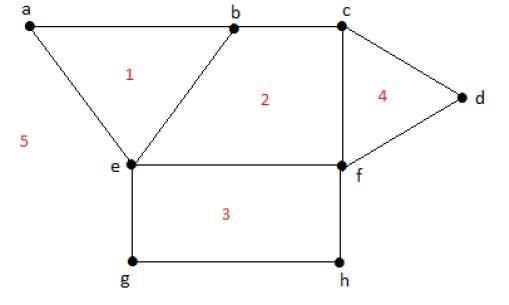
경계 영역의 정도 r = deg(r) = 영역을 둘러싸는 가장자리 수 r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8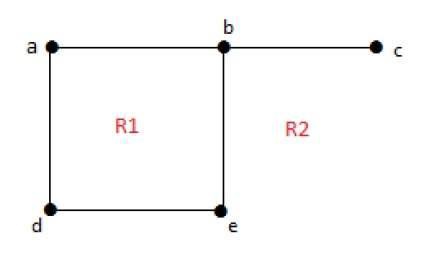
무한 영역의 정도 r = deg(r) = 영역을 둘러싸는 가장자리 수 r.
deg(R1) = 4
deg(R2) = 6평면 그래프에서 다음 속성은 양호합니다.
'n'정점이있는 평면 그래프에서 모든 정점의 각도 합계는 다음과 같습니다.
에 따르면 Sum of Degrees of Regions/ 정리, 'n'영역이있는 평면 그래프에서 영역의 합은 다음과 같습니다.
위의 정리를 바탕으로 다음과 같은 결론을 내릴 수 있습니다.
평면 그래프에서
각 영역의 차수가 K이면 영역의 차수의 합은-
각 영역의 차수가 K (≥ K) 이상이면
각 영역의 차수가 기껏해야 K (≤ K)이면
Note − 모든 지역의 차수가 같다고 가정합니다.
에 따르면 Euler’s Formulae 평면형 그래프에서
그래프 'G'가 연결된 평면형이면
'K'성분이 포함 된 평면형 그래프의 경우
여기서 | V | 정점의 수, | E | 은 모서리의 수이고 | R | 지역 수입니다.
가장자리 정점 부등식
'G'가 각 영역의 정도가 'K'이상인 연결된 평면 그래프이면,
| E | ≤ k / (k-2) {| v | -2}
알다시피 | V | + | R | = | E | + 2
K. | R | ≤ 2 | E |
K (| E |-| V | + 2) ≤ 2 | E |
(K-2) | E | ≤ K (| V |-2)
| E | ≤ k / (k-2) {| v | -2}
'G'가 단순 연결된 평면 그래프 인 경우
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4deg (V) ≤ 5 인 꼭지점 V • ∈ G가 하나 이상 있습니다.
'G'가 단순 연결된 평면 그래프 (최소 2 개의 모서리 포함)이고 삼각형이없는 경우
|E| ≤ {2|V| – 4}Kuratowski의 정리
그래프 'G'는 'G'에 K 5 또는 K 3,3에 동종인 부분 그래프가있는 경우에만 비 평면형 입니다.
동형
G의 일부 모서리를 더 많은 꼭짓점으로 나누어 동일한 그래프 'G'에서 각 그래프를 얻을 수있는 경우 두 그래프 G 1 및 G 2 는 동형이라고합니다. 다음 예를 살펴보십시오-

하나의 정점을 추가하여 가장자리 'rs'를 두 개의 가장자리로 나눕니다.
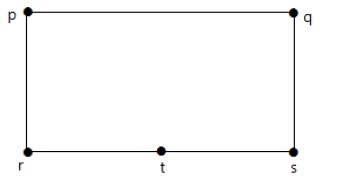
아래에 표시된 그래프는 첫 번째 그래프와 동형입니다.
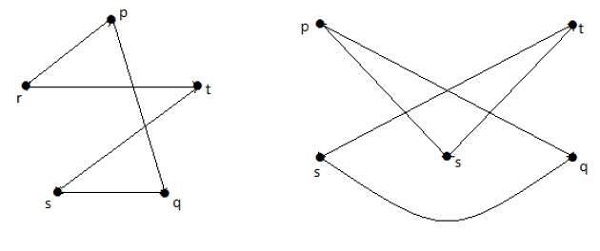
G 1 이 G 2 에 대해 동형 인 경우 G는 G2에 대해 동형이지만 그 반대가 사실 일 필요는 없습니다.
꼭지점이 4 개 이하인 모든 그래프는 평면입니다.
모서리가 8 개 이하인 모든 그래프는 평면입니다.
완전한 그래프 K n 은 n ≤ 4 인 경우에만 평면입니다.
완전한 이분 그래프 K m, n 은 m ≤ 2 또는 n ≤ 2 인 경우에만 평면입니다.
최소 정점 수가있는 단순한 비평면 그래프는 완전한 그래프 K 5 입니다.
최소 간선 수가있는 단순 비평면 그래프는 K 3, 3 입니다.
다면체 그래프
단순한 연결 평면 그래프는 각 꼭지점의 차수가 ≥ 3, 즉 deg (V) ≥ 3 ∀ V ∈ G 인 경우 다면체 그래프라고합니다.
3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |
동일한 경로를 다시 추적하지 않고 모든 정점 사이에 경로를 그릴 수 있으면 그래프를 횡단 할 수 있습니다. 이 경로를 기반으로이 장에서 설명하는 Euler의 경로 및 Euler의 회로와 같은 몇 가지 범주가 있습니다.
오일러의 길
오일러의 경로에는 'G'의 각 가장자리가 정확히 한 번 포함되고 'G'의 각 꼭지점이 적어도 한 번 포함됩니다. 연결된 그래프 G는 오일러의 경로를 포함하는 경우 횡단 가능하다고합니다.
Example
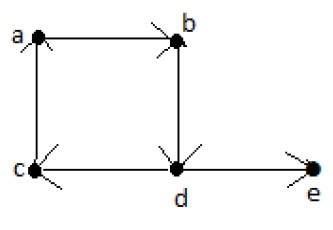
오일러의 경로 = dcabde.
오일러의 회로
오일러 경로에서 시작 정점이 끝 정점과 같으면이를 오일러 회로라고합니다.
Example
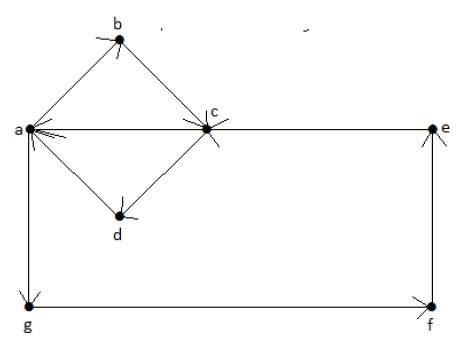
Euler’s Path = abcdagfeca.
오일러의 회로 정리
연결된 그래프 'G'는 G에서 홀수 차수가있는 정점의 수가 정확히 2 또는 0 인 경우에만 횡단 할 수 있습니다. 연결된 그래프 G는 오일러의 경로를 포함 할 수 있지만 오일러의 회로는 포함 할 수 없습니다. 이상한 정도.
Note −이 오일러 경로는 홀수도의 정점으로 시작하여 홀수도의 다른 정점으로 끝납니다.
Example
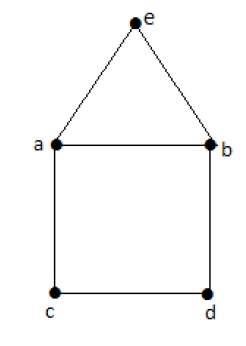
Euler’s Path− beabdca는 Euler의 회로가 아니지만 Euler의 경로입니다. 분명히 정확히 2 개의 홀수도 정점이 있습니다.
Note − 연결된 그래프 G에서 홀수 차수의 정점 수가 0이면 오일러 회로가 존재합니다.
해밀턴 그래프
연결된 그래프 G는 G의 모든 꼭지점을 포함하는주기가있는 경우 해밀턴 그래프라고합니다.
모든 사이클은 회로이지만 회로는 여러 사이클을 포함 할 수 있습니다. 이러한주기를Hamiltonian cycle of G.
해밀턴 경로
연결된 그래프는 G의 각 꼭지점을 정확히 한 번만 포함하면 Hamiltonian이라고합니다. 이러한 경로를Hamiltonian path.
Example
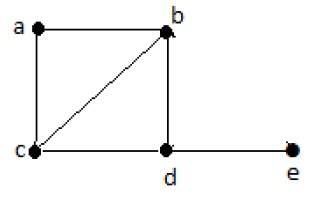
Hamiltonian Path− edbac.
Note
오일러의 회로는 정확히 한 번 그래프의 각 모서리를 포함합니다.
Hamiltonian주기에서 그래프의 일부 간선을 건너 뛸 수 있습니다.
Example
다음 그래프를보세요-
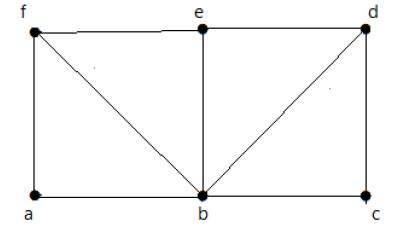
위에 표시된 그래프의 경우-
오일러 경로가 있음 – 거짓
오일러 회로가 있음 – 거짓
해밀턴주기가 존재합니다 – 사실
해밀턴의 길은 존재합니다 – 사실
G에는 각도가 홀수 인 4 개의 정점이 있으므로 횡단 할 수 없습니다. 내부 모서리를 건너 뛰면 그래프는 모든 정점을 통과하는 해밀턴 순환을 갖습니다.
이 장에서는 이전 장에서 이미 논의한 개념을 보여주는 몇 가지 표준 예제를 다룰 것입니다.
예 1
Find the number of spanning trees in the following graph.
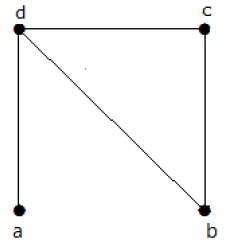
해결책
위 그래프에서 얻은 스패닝 트리의 개수는 3 개입니다.
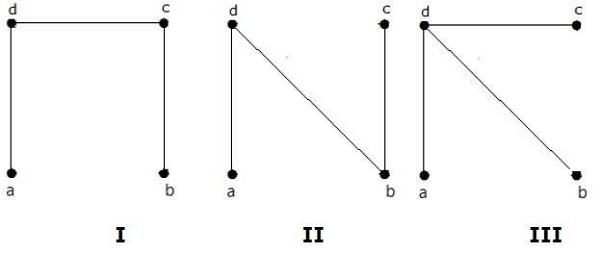
이 세 가지는 주어진 그래프에 대한 스패닝 트리입니다. 여기서 그래프 I와 II는 서로 동형입니다. 분명히 비 동형 스패닝 트리의 수는 2 개입니다.
예 2
How many simple non-isomorphic graphs are possible with 3 vertices?
해결책
3 개의 정점으로 가능한 4 개의 비 동형 그래프가 있습니다. 아래에 나와 있습니다.
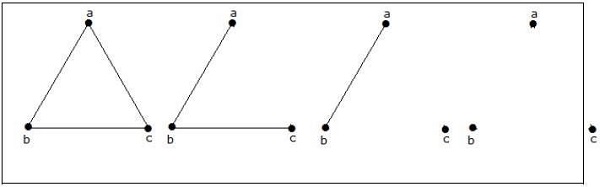
예제 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
해결책
학위 정리의 합으로,
20 Σ i = 1 deg (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
오일러의 공식에 따르면
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
따라서 지역 수는 12 개입니다.
예 4
What is the chromatic number of complete graph Kn?
해결책
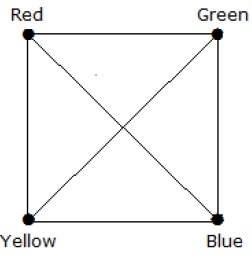
완전한 그래프에서 인접한 각 정점은 남아있는 (n-1) 정점입니다. 따라서 각 정점에는 새로운 색상이 필요합니다. 따라서, K 색 번호 N = N.
예 5
What is the matching number for the following graph?
해결책
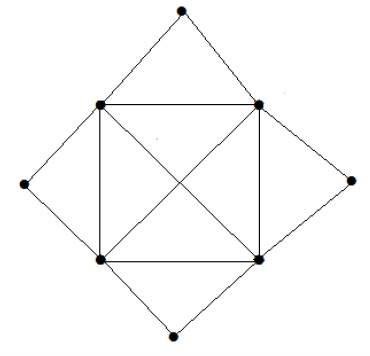
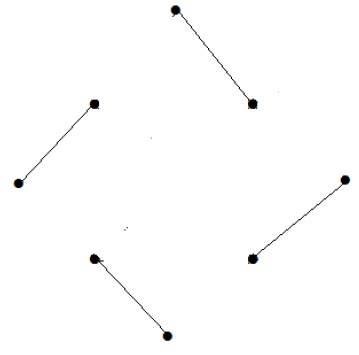
정점 수 = 9
8 개의 정점 만 일치시킬 수 있습니다.
일치하는 숫자는 4입니다.
예제 6
What is the line covering number of for the following graph?
해결책
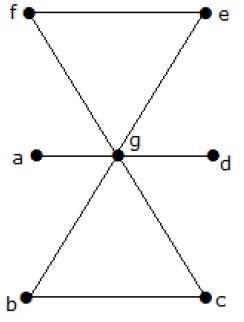
정점 수 = | V | = n = 7
라인 커버링 번호 = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
3 개의 모서리를 사용하여 모든 정점을 덮을 수 있습니다.
따라서 선을 덮는 번호는 3입니다.