그래프 이론-독립 세트
독립 세트는 세트로 표시됩니다.
없어야한다 any edges adjacent to each other. 두 모서리 사이에 공통 정점이 없어야합니다.
없어야한다 any vertices adjacent to each other. 두 정점 사이에 공통 가장자리가 없어야합니다.
독립 라인 세트
'G'= (V, E)를 그래프라고합시다. L의 두 모서리가 인접하지 않은 경우 E의 부분 집합 L을 'G'의 독립 선 집합이라고합니다. 이러한 세트를 독립 라인 세트라고합니다.
Example
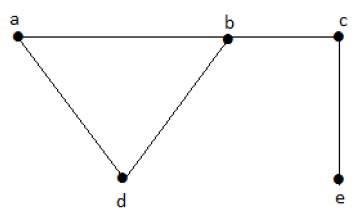
다음 하위 집합을 고려해 보겠습니다.
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}이 예에서 하위 집합 L2 및 L3은 주어진 그래프에서 분명히 인접한 간선이 아닙니다. 그들은 독립적 인 라인 세트입니다. 그러나 L1은 독립된 선 집합이 아니므로 독립 선 집합을 만들려면 가장자리가 두 개 이상 있어야합니다.
최대 독립 라인 세트
독립 선 집합은 'G'의 다른 모서리를 'L'에 추가 할 수없는 경우 그래프 'G'의 최대 독립 선 집합이라고합니다.
Example
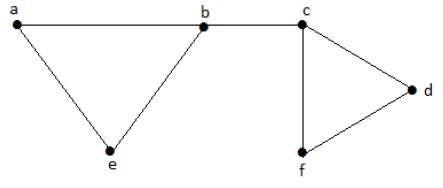
다음 하위 집합을 고려해 보겠습니다.
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L 2 및 L 3 은 최대 독립 라인 세트 / 최대 일치입니다. 이 두 하위 집합 만 인접하지 않은 다른 가장자리를 추가 할 기회가 없습니다. 따라서이 두 하위 집합은 최대 독립 선 집합으로 간주됩니다.
최대 독립 라인 세트
최대 모서리 수를 가진 'G'의 최대 독립 라인 세트를 'G'의 최대 독립 라인 세트라고합니다.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
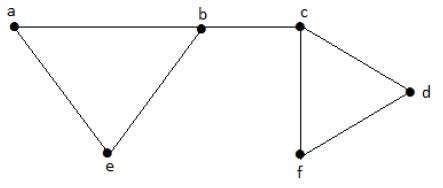
다음 하위 집합을 고려해 보겠습니다.
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L 3 은 그래프에서 인접 모서리가 아닌 최대 모서리가있는 G의 최대 독립 선 세트이며 β1 = 3으로 표시됩니다.
Note − 고립 된 정점이없는 그래프 G의 경우
α1 + β1 = 그래프의 꼭지점 수 = | V |
Example
라인 커버링 수 K n / C n / w n ,
$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \ : if \ : n \ : is \ : even \\\ frac {n + 1} {2} \ : if \ : n \ : is \ : odd \ end {cases} $$라인 독립 수 (일치하는 수) = β 1 = [n / 2] α 1 + β 1 = n.
독립 정점 세트
'G'= (V, E)를 그래프라고합시다. 'S'의 두 꼭지점이 인접하지 않은 경우 'V'의 하위 집합을 'G'의 독립적 인 집합이라고합니다.
Example

위의 그래프에서 다음 하위 집합을 고려하십시오-
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}분명히 S 1 은 독립적 인 꼭지점 집합이 아닙니다. 왜냐하면 독립적 인 꼭지점 집합을 얻으려면 그래프에서에 최소한 두 개의 꼭지점이 있어야하기 때문입니다. 그러나 여기서는 그렇지 않습니다. 부분 집합 S 2 , S 3 , S 4 는 부분 집합의 한 꼭지점에 인접한 꼭지점이 없기 때문에 독립적 인 꼭지점 집합입니다.
최대 독립 정점 세트
'G'를 그래프라고하면 'G'의 다른 정점을 'S'에 추가 할 수없는 경우 'G'의 독립적 인 정점 집합이 최대라고합니다.
Example
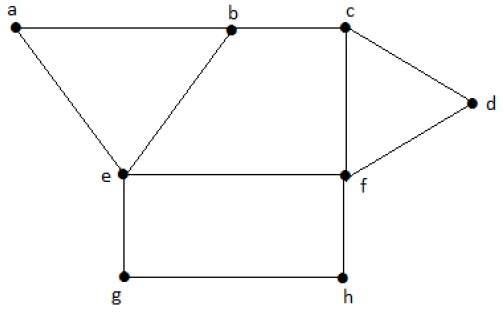
위 그래프에서 다음 하위 집합을 고려하십시오.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 2 및 S 3 은 'G'의 최대 독립 정점 세트입니다. S 1 과 S 4 에서 다른 정점을 추가 할 수 있습니다. 그러나 S 2 와 S 3 에서는 다른 정점을 추가 할 수 없습니다.
최대 독립 정점 세트
최대 정점 수를 가진 'G'의 최대 독립 정점 집합을 최대 독립 정점 집합이라고합니다.
Example

위의 그래프에서 다음 하위 집합을 고려하십시오.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 3 만이 가장 많은 수의 정점을 포함하므로 최대 독립 정점 세트입니다. 'G'의 최대 독립 정점 세트에있는 정점의 수를 G의 독립 정점 수 (β 2 )라고합니다.
Example
전체 그래프 K n ,
정점 커버링 수 = α 2 = n−1
정점 독립 수 = β 2 = 1
α 2 + β 2 = n이 있습니다.
완전한 그래프에서 각 정점은 나머지 (n-1) 정점에 인접 해 있습니다. 따라서 K n 의 최대 독립 집합 에는 꼭지점이 하나만 포함됩니다.
따라서 β 2 = 1
및 α 2 = | v | − β 2 = n-1
Note − 모든 그래프 'G'= (V, E)
- α 2 + β 2 = | v |
- 'S'가 'G'의 독립 정점 세트 인 경우 (V – S)는 G의 정점 커버입니다.