그래프 이론-그래프 유형
정점 수, 모서리 수, 상호 연결성 및 전체 구조에 따라 다양한 유형의 그래프가 있습니다. 이 장에서는 몇 가지 중요한 그래프 유형에 대해서만 설명합니다.
널 그래프
A graph having no edges Null 그래프라고합니다.
예

위의 그래프에는 'a', 'b', 'c'라는 세 개의 꼭지점이 있지만 그 사이에 가장자리가 없습니다. 따라서 그것은 Null 그래프입니다.
사소한 그래프
ㅏ graph with only one vertex Trivial Graph라고합니다.
예

위에 표시된 그래프에는 다른 모서리가없는 꼭지점 'a'가 하나만 있습니다. 따라서 그것은 사소한 그래프입니다.
무 방향 그래프
무 방향 그래프는 간선을 포함하지만 간선은 방향성이 아닙니다.
예
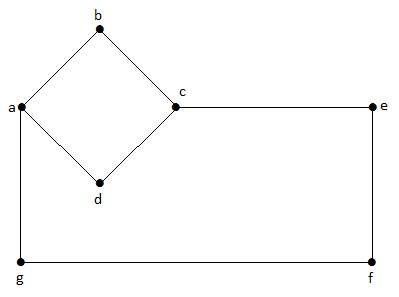
이 그래프에서 'a', 'b', 'c', 'd', 'e', 'f', 'g'는 꼭지점이고 'ab', 'bc', 'cd', 'da ','ag ','gf ','ef '는 그래프의 가장자리입니다. 무 방향 그래프이기 때문에 'ab'와 'ba'간선은 동일합니다. 마찬가지로 다른 모서리도 같은 방식으로 고려됩니다.
유향 그래프
유 방향 그래프에서 각 간선에는 방향이 있습니다.
예

위 그래프에는 7 개의 꼭지점 'a', 'b', 'c', 'd', 'e', 'f', 'g'와 8 개의 모서리 'ab', 'cb', ' dc ','ad ','ec ','fe ','gf '및'ga '. 방향성 그래프이기 때문에 각 모서리에는 방향을 나타내는 화살표 표시가 있습니다. 유 방향 그래프에서 'ab'는 'ba'와 다릅니다.
간단한 그래프
그래프 with no loops 그리고 아니 parallel edges 단순 그래프라고합니다.
'n'개의 꼭지점이있는 단일 그래프에서 가능한 최대 간선 수는 n C 2 이며 여기서 n C 2 = n (n – 1) / 2입니다.
'n'꼭지점 = 2 n c 2 = 2 n (n-1) / 2로 가능한 단순 그래프의 수입니다 .
예
다음 그래프에는 평행 모서리와 루프를 제외하고 최대 값 인 3 개의 모서리가있는 3 개의 꼭지점이 있습니다. 이것은 위의 공식을 사용하여 증명할 수 있습니다.
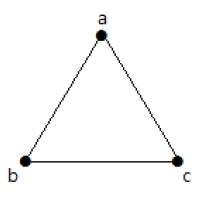
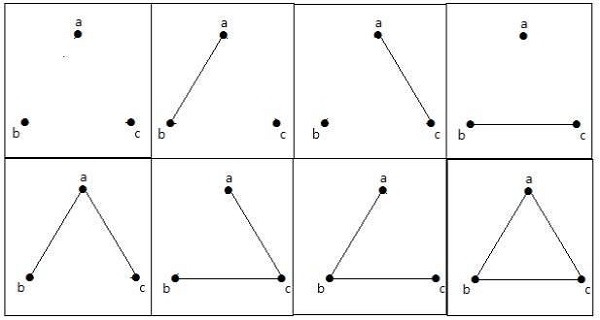
n = 3 꼭지점을 가진 가장자리의 최대 수-
n = 3 꼭짓점을 가진 단순 그래프의 최대 수-
이 8 개의 그래프는 아래와 같습니다.
연결된 그래프
그래프 G가 연결되었다고합니다 if there exists a path between every pair of vertices. 그래프의 모든 정점에 대해 최소한 하나의 가장자리가 있어야합니다. 그래서 우리는 그것이 가장자리의 다른쪽에있는 다른 정점에 연결되어 있다고 말할 수 있습니다.
예
다음 그래프에서 각 정점에는 다른 가장자리에 연결된 자체 가장자리가 있습니다. 따라서 연결된 그래프입니다.

연결이 끊긴 그래프
연결된 꼭지점이 2 개 이상 포함되지 않은 경우 그래프 G는 연결이 끊어집니다.
예 1
다음 그래프는 'a', 'b', 'c', 'd'꼭지점이있는 구성 요소와 'e', 'f', 'g'가있는 두 개의 구성 요소가있는 연결이 끊긴 그래프의 예입니다. 'h'꼭지점.
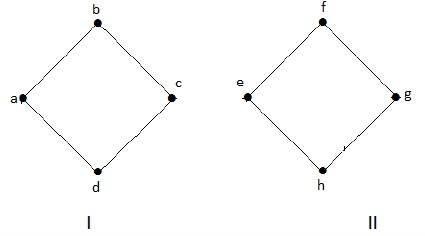
두 구성 요소는 독립적이며 서로 연결되어 있지 않습니다. 따라서이를 단절된 그래프라고합니다.
예 2

이 예에는 서로 연결되지 않은 두 개의 독립적 인 구성 요소 abfe와 cd가 있습니다. 따라서 이것은 연결이 끊어진 그래프입니다.
일반 그래프
그래프 G는 규칙적이라고합니다. if all its vertices have the same degree. 그래프에서 각 꼭지점의 차수가 'k'이면 그래프를 'k- 정규 그래프'라고합니다.
예
다음 그래프에서 모든 정점의 차수는 동일합니다. 따라서 이러한 그래프를 일반 그래프라고합니다.
두 그래프에서 모든 정점은 차수가 2입니다.이를 2- 정규 그래프라고합니다.
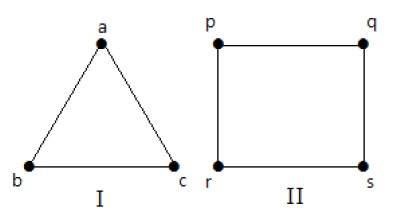
완전한 그래프
'n'상호 정점이있는 간단한 그래프를 완전한 그래프라고하며 denoted by ‘Kn’. 그래프에서a vertex should have edges with all other vertices, 완전한 그래프라고 불렀습니다.
즉, 꼭지점이 그래프의 다른 모든 꼭지점에 연결되어 있으면 완전한 그래프라고합니다.
예
다음 그래프에서 그래프의 각 정점은 그 자체를 제외하고 그래프의 나머지 모든 정점과 연결됩니다.
그래프 I에서
| ㅏ | 비 | 씨 | |
|---|---|---|---|
| ㅏ | 연결되지 않은 | 연결됨 | 연결됨 |
| 비 | 연결됨 | 연결되지 않은 | 연결됨 |
| 씨 | 연결됨 | 연결됨 | 연결되지 않은 |
그래프 II에서
| 피 | 큐 | 아르 자형 | 에스 | |
|---|---|---|---|---|
| 피 | 연결되지 않은 | 연결됨 | 연결됨 | 연결됨 |
| 큐 | 연결됨 | 연결되지 않은 | 연결됨 | 연결됨 |
| 아르 자형 | 연결됨 | 연결됨 | 연결되지 않은 | 연결됨 |
| 에스 | 연결됨 | 연결됨 | 연결됨 | 연결되지 않은 |
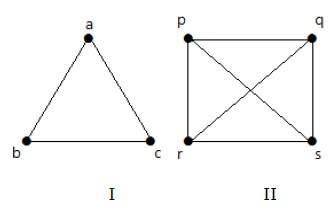
사이클 그래프
'n'꼭지점 (n> = 3) 및 'n'가장자리가있는 간단한 그래프는 모든 가장자리가 길이 'n'의주기를 형성하는 경우주기 그래프라고합니다.
그래프의 각 꼭지점의 차수가 2 인 경우이를주기 그래프라고합니다.
Notation− C n
예
다음 그래프를 살펴보십시오.
그래프 I에는 'ab-bc-ca'주기를 형성하는 3 개의 모서리가있는 3 개의 꼭지점이 있습니다.
그래프 II에는 'pq-qs-sr-rp'주기를 형성하는 4 개의 모서리가있는 4 개의 꼭지점이 있습니다.
그래프 III에는 'ik-km-ml-lj-ji'주기를 형성하는 5 개의 모서리가있는 5 개의 꼭지점이 있습니다.

따라서 주어진 모든 그래프는 사이클 그래프입니다.
휠 그래프
바퀴 그래프는 새 정점을 추가하여 사이클 그래프 C n-1 에서 얻습니다 . 그 새로운 정점은Hub이것은 C n 의 모든 정점에 연결됩니다 .
표기법-W n
W의 가장자리 수 n = 허브에서 다른 모든 정점까지의 가장자리 수 +
허브가없는 사이클 그래프에서 다른 모든 노드의 에지 수입니다.
= (n–1) + (n–1)
= 2 (n–1)
예
다음 그래프를 살펴보십시오. 그들은 모두 바퀴 그래프입니다.
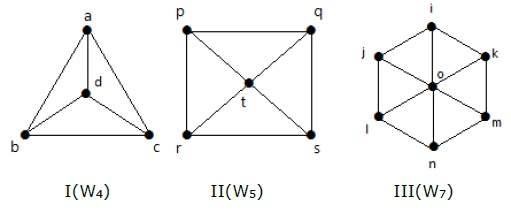
그래프 I에서는 'd'라는 중간에 꼭짓점을 추가하여 C 3 에서 얻습니다 . W 4 로 표시됩니다 .
W4의 모서리 수 = 2 (n-1) = 2 (3) = 6
그래프 II에서는 중간에 't'라는 정점을 추가하여 C4에서 구합니다. W 5 로 표시됩니다 .
W5의 모서리 수 = 2 (n-1) = 2 (4) = 8
그래프 III에서는 'o'라는 중간에 꼭지점을 추가하여 C 6 에서 얻습니다 . W 7 로 표시됩니다 .
W4의 모서리 수 = 2 (n-1) = 2 (6) = 12
순환 그래프
그래프 with at least one 주기를 순환 그래프라고합니다.
예
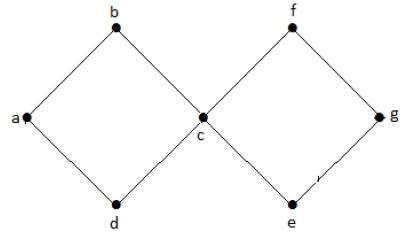
위의 예제 그래프에는 abcda와 cfgec의 두 사이클이 있습니다. 따라서 순환 그래프라고합니다.
비순환 그래프
그래프 with no cycles 비순환 그래프라고합니다.
예
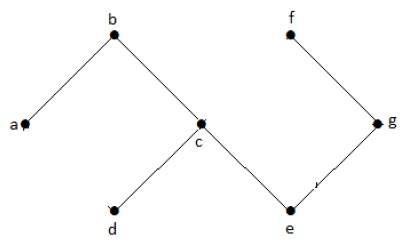
위의 예제 그래프에는 사이클이 없습니다. 따라서 비순환 그래프입니다.
이분 그래프
정점 분할 V = {V 1 , V 2 }가 있는 간단한 그래프 G = (V, E)를 이분 그래프라고합니다.if every edge of E joins a vertex in V1 to a vertex in V2.
일반적으로 Bipertite 그래프에는 V1과 V2의 두 세트의 정점이 있으며 가장자리가 그려지면 세트 V 1의 모든 정점을 V 2 세트의 정점에 연결해야합니다 .
예
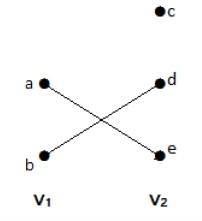
이 그래프에서 두 세트의 꼭지점 V 1 과 V 2를 관찰 할 수 있습니다 . 여기서 'ae'와 'bd'라는 이름의 두 모서리는 두 세트 V 1 및 V 2 의 정점을 연결합니다 .
완전한 이분 그래프
분할이 V = {V 1 , V 2 } 인 이분 그래프 'G', G = (V, E) 는 V 1의 모든 정점이 V 2의 모든 정점에 연결 되면 완전한 이분 그래프라고합니다 .
일반적으로 완전한 이분 그래프는 세트 V 1의 각 정점을 세트 V 2의 각 정점에 연결합니다 .
예
다음 그래프는 세트 V 1의 각 정점을 세트 V 2의 각 정점에 연결하는 간선이 있기 때문에 완전한 이분 그래프 입니다.
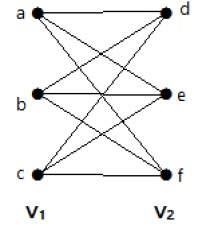
| V 1 | = m 및 | V 2 | = n이면 완전한 이분 그래프는 K m, n으로 표시됩니다 .
- K m, n 에는 (m + n) 꼭지점과 (mn) 가장자리가 있습니다.
- K m, n 은 m = n 인 경우 일반 그래프입니다.
일반적으로 complete bipartite graph is not a complete graph.
m = n = 1 인 경우 K m, n 은 완전한 그래프입니다.
n 개의 정점이있는 이분 그래프의 최대 간선 수는 다음과 같습니다.
[N 2 / 4]
n = 10, k5, 5 = [n2 / 4] = [10 2 / 4] = 25.
마찬가지로 K6, 4 = 24
K7, 3 = 21
K8, 2 = 16
K9, 1 = 9
n = 9이면 k5, 4 = [n2 / 4] = [92/4] = 20
마찬가지로 K6, 3 = 18
K7, 2 = 14
K8, 1 = 8
'G'에 홀수 길이의주기가없는 경우 'G'는 이분 그래프입니다. 이분 그래프의 특별한 경우는 별 그래프입니다.
스타 그래프
K1, n-1 형식의 완전한 이분 그래프는 n- 꼭지점이있는 별 그래프입니다. 단일 정점이 한 세트에 속하고 나머지 모든 정점이 다른 세트에 속하는 경우 스타 그래프는 완전한 이분 그래프입니다.
예
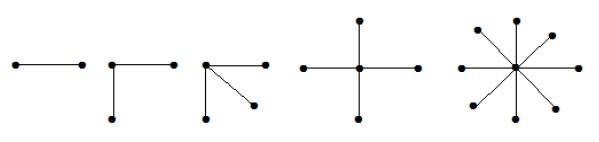
위의 그래프에서 'n'정점 중 모든 'n–1'정점은 단일 정점에 연결됩니다. 따라서 별 그래프 인 K 1 , n-1 의 형태입니다 .
그래프 보완
'G-'를 'G'와 같은 일부 정점이있는 간단한 그래프로, 'G-'에 {U, V}가있는 가장자리가 G에 없으면 두 개의 정점이 인접 해 있음을 의미합니다. 두 꼭지점이 G에서 인접하지 않은 경우 'G-'에서.
그래프 I에 존재하는 간선이 다른 그래프 II에없고 그래프 I와 그래프 II가 함께 결합되어 완전한 그래프를 형성하는 경우 그래프 I와 그래프 II를 서로의 보수라고합니다.
예
다음 예에서 graph-I에는 두 개의 간선 'cd'와 'bd'가 있습니다. 보완 그래프 II에는 네 개의 간선이 있습니다.
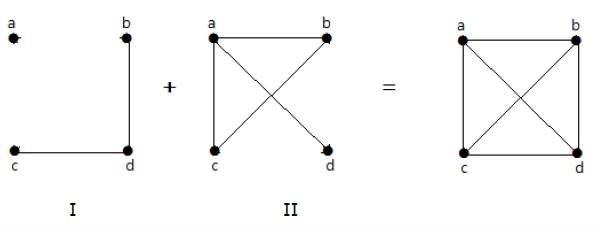
그래프 I의 간선은 그래프 II에 나타나지 않으며 그 반대의 경우도 마찬가지입니다. 따라서 두 그래프의 조합은 'n'꼭지점의 완전한 그래프를 제공합니다.
Note − 두 개의 보완적인 그래프의 조합은 완전한 그래프를 제공합니다.
'G'가 간단한 그래프이면
| E (G) | + | E ( 'G-') | = | E (Kn) |, 여기서 n = 그래프의 꼭지점 수.
예
'G'를 9 개의 꼭지점과 12 개의 모서리가있는 간단한 그래프라고 가정하고 'G-'의 모서리 수를 찾으십시오.
당신은 | E (G) | + | E ( 'G-') | = | E (Kn) |
12 + | E ( 'G-') | =
9 (9-1) / 2 = 9 C 2
12 + | E ( 'G-') | = 36
| E ( 'G-') | = 24
'G'는 40 개의 간선이있는 간단한 그래프이고 그 보수 'G-'에는 38 개의 간선이 있습니다. 그래프 G 또는 'G-'에서 꼭지점 수를 찾으십시오.
그래프의 꼭지점 수를 'n'으로 지정합니다.
| E (G) | + | E ( 'G-') | = | E (Kn) |
40 + 38 = n (n-1) / 2
156 = n (n-1)
13 (12) = n (n-1)
n = 13