그래프 이론-기초
그래프는 점과 점에 연결된 선의 다이어그램입니다. 정점이 연결되지 않은 두 정점 세트를 연결하는 선이 하나 이상 있습니다. 그래프 이론에서 그래프의 개념은 점, 선, 꼭지점, 가장자리, 꼭지점의 정도, 그래프의 속성 등과 같은 몇 가지 기본 용어를 기반으로합니다. 여기이 장에서는 이러한 그래프 이론의 기본 사항을 다룹니다.
포인트
A point1 차원, 2 차원 또는 3 차원 공간의 특정 위치입니다. 더 나은 이해를 위해 점을 알파벳으로 표시 할 수 있습니다. 점으로 표시 할 수 있습니다.
예

여기서 점은 'a'라는 점입니다.
선
ㅏ Line두 지점 사이의 연결입니다. 실선으로 표시 할 수 있습니다.
Example

여기서 'a'와 'b'는 포인트입니다. 이 두 지점 사이의 연결을 선이라고합니다.
꼭지점
정점은 여러 선이 만나는 지점입니다. 그것은 또한node. 점과 유사하게 정점도 알파벳으로 표시됩니다.
Example

여기서 정점은 알파벳 'a'로 명명됩니다.
가장자리
가장자리는 두 정점을 연결하는 선에 대한 수학적 용어입니다. 단일 정점에서 많은 모서리를 형성 할 수 있습니다. 꼭지점이 없으면 가장자리를 만들 수 없습니다. 가장자리에 대한 시작 정점과 끝 정점이 있어야합니다.
Example

여기서 'a'와 'b'는 두 꼭지점이며 이들 사이의 링크를 가장자리라고합니다.
그래프
그래프 'G'는 G = (V, E)로 정의됩니다. 여기서 V는 모든 정점의 집합이고 E는 그래프의 모든 모서리 집합입니다.
Example 1

위의 예에서 ab, ac, cd 및 bd는 그래프의 간선입니다. 마찬가지로 a, b, c 및 d는 그래프의 꼭지점입니다.
Example 2
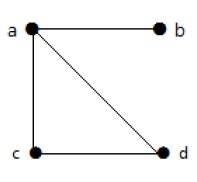
이 그래프에는 네 개의 꼭지점 a, b, c, d와 네 개의 모서리 ab, ac, ad, cd가 있습니다.
고리
그래프에서 모서리가 정점에서 그 자체로 그려지는 경우이를 루프라고합니다.
Example 1

위의 그래프에서 V는 루프를 형성하는 모서리 (V, V)가있는 정점입니다.
Example 2

이 그래프에는 꼭지점 a와 꼭지점 b에 형성된 두 개의 루프가 있습니다.
정점의 정도
정점 V에 인접한 정점의 수입니다.
Notation − deg (V).
n 개의 정점이있는 간단한 그래프에서 모든 정점의 차수는 다음과 같습니다.
deg (v) ≤ n – 1 ∀ v ∈ G
정점은 그 자체를 제외하고 다른 모든 정점과 함께 가장자리를 형성 할 수 있습니다. 따라서 정점의 정도는number of vertices in the graph minus 1. 이 1은 자체적으로 루프를 형성 할 수 없으므로 자체 정점 용입니다. 정점에 루프가있는 경우 단순 그래프가 아닙니다.
정점의 정도는 그래프의 두 가지 경우에서 고려할 수 있습니다.
무 방향 그래프
유향 그래프
무 방향 그래프의 정점 각도
무 방향 그래프에는 유 방향 간선이 없습니다. 다음 예를 고려하십시오.
Example 1
다음 그래프를보세요-

위의 무 방향 그래프에서
deg (a) = 2, 꼭지점 'a'에서 만나는 2 개의 모서리가 있기 때문입니다.
deg (b) = 3, 꼭지점 'b'에서 만나는 3 개의 가장자리가 있기 때문입니다.
deg (c) = 1, 꼭지점 'c'에 1 개의 모서리가 형성됨
그래서 'c'는 pendent vertex.
deg (d) = 2, 꼭지점 'd'에서 만나는 2 개의 가장자리가 있기 때문입니다.
deg (e) = 0, 꼭지점 'e'에 0 개의 가장자리가 있기 때문입니다.
그래서 'e'는 isolated vertex.
Example 2
다음 그래프를보세요-

위 그래프에서
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2, deg (e) = 0입니다.
정점 'e'는 격리 된 정점입니다. 그래프에는 늘어진 꼭지점이 없습니다.
유향 그래프의 꼭지점 각도
유 방향 그래프에서 각 정점에는 indegree 그리고 outdegree.
그래프의 정도
Indegree of vertex V는 정점 V로 들어오는 가장자리의 수입니다.
Notation −도 − (V).
그래프의 이탈
Outdegree of vertex V는 꼭지점 V에서 나가는 가장자리의 수입니다.
Notation − deg + (V).
다음 예를 고려하십시오.
Example 1
다음 유향 그래프를 살펴보십시오. 꼭지점 'a'에는 바깥쪽으로가는 'ad'와 'ab'의 두 모서리가 있습니다. 따라서 그것의 outdegree는 2입니다. 마찬가지로, 꼭지점 'a'쪽으로 오는 가장자리 'ga'가 있습니다. 따라서 'a'의 정도는 1입니다.

다음 표는 다른 정점의 부도 및 외도를 보여줍니다.
| 꼭지점 | 맞지 않음 | 이상 |
|---|---|---|
| ㅏ | 1 | 2 |
| 비 | 2 | 0 |
| 씨 | 2 | 1 |
| 디 | 1 | 1 |
| 이자형 | 1 | 1 |
| 에프 | 1 | 1 |
| 지 | 0 | 2 |
Example 2
다음 유향 그래프를 살펴보십시오. 꼭지점 'a'에는 꼭지점 'a'에서 바깥쪽으로가는 가장자리 'ae'가 있습니다. 따라서 그 외각은 1입니다. 마찬가지로 그래프에는 정점 'a'를 향하는 가장자리 'ba'가 있습니다. 따라서 'a'의 정도는 1입니다.

다음 표는 다른 정점의 부도 및 외도를 보여줍니다.
| 꼭지점 | 맞지 않음 | 이상 |
|---|---|---|
| ㅏ | 1 | 1 |
| 비 | 0 | 2 |
| 씨 | 2 | 0 |
| 디 | 1 | 1 |
| 이자형 | 1 | 1 |
늘어진 꼭지점
정점의 정도를 사용하여 두 가지 특수한 유형의 정점을 갖게됩니다. 차수가 1 인 정점을 펜던트 정점이라고합니다.
Example

여기이 예에서 꼭지점 'a'와 꼭지점 'b'는 연결된 가장자리 'ab'를 갖습니다. 따라서 꼭지점 'a'에 대해서는 꼭지점 'b'를 향하는 가장자리가 하나 뿐이고 꼭지점 'b'에 대해서도 마찬가지로 꼭지점 'a'에 대한 가장자리가 하나뿐입니다. 마지막으로 꼭지점 'a'와 꼭지점 'b'는 돌출 꼭지점이라고도하는 1 차도를 갖습니다.
격리 된 정점
차수가 0 인 정점을 격리 된 정점이라고합니다.
Example

여기서 정점 'a'와 정점 'b'는 서로 연결되어 있지 않으며 다른 정점과도 연결되어 있지 않습니다. 따라서 'a'와 'b'꼭짓점의 차수는 모두 0입니다. 이들은 분리 된 정점이라고도합니다.
인접
다음은 인접성의 규범입니다-
그래프에서 두 개의 정점은 adjacent, 두 정점 사이에 가장자리가있는 경우. 여기서 정점의 인접성은 두 정점을 연결하는 단일 가장자리에 의해 유지됩니다.
그래프에서 두 모서리 사이에 공통 꼭지점이있는 경우 두 모서리는 인접 해 있다고합니다. 여기서 가장자리의 인접성은 두 가장자리를 연결하는 단일 정점에 의해 유지됩니다.
Example 1
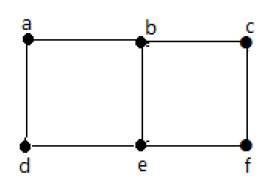
위의 그래프에서-
'a'와 'b'는 인접한 정점입니다. 그 사이에 공통 모서리 'ab'이 있기 때문입니다.
'a'와 'd'는 인접한 정점입니다. 그 사이에 공통 가장자리 'ad'가 있기 때문입니다.
ab '와'be '는 그 사이에 공통 꼭지점'b '가 있기 때문에 인접한 가장자리입니다.
be '와'de '는 그 사이에 공통 꼭지점'e '가 있기 때문에 인접한 가장자리입니다.
Example 2
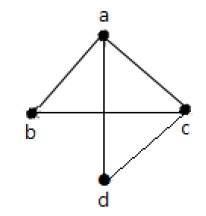
위의 그래프에서-
'a'와 'd'는 인접한 정점입니다. 그 사이에 공통 가장자리 'ad'가 있기 때문입니다.
'c'와 'b'는 인접한 정점입니다. 그 사이에 공통 가장자리 'cb'가 있기 때문입니다.
'ad'와 'cd'는 그 사이에 공통 꼭지점 'd'가 있기 때문에 인접한 가장자리입니다.
'ac'와 'cd'는 그 사이에 공통 꼭지점 'c'가 있기 때문에 인접한 가장자리입니다.
평행 모서리
그래프에서 한 쌍의 꼭지점이 둘 이상의 가장자리로 연결된 경우 이러한 가장자리를 평행 가장자리라고합니다.
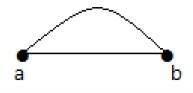
위의 그래프에서 'a'와 'b'는 두 개의 모서리 'ab'와 'ab'사이에 연결된 두 개의 꼭지점입니다. 따라서 평행 모서리라고합니다.
멀티 그래프
평행 모서리가있는 그래프를 다중 그래프라고합니다.
Example 1

위 그래프에는 'ab', 'ac', 'cd', 'cd', 'bd'의 5 개의 간선이 있습니다. 'c'와 'd'사이에 두 개의 평행 한 모서리가 있으므로 Multigraph입니다.
Example 2
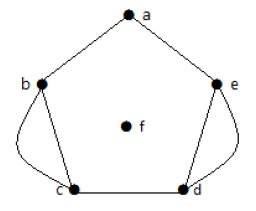
위 그래프에서 꼭지점 'b'와 'c'에는 두 개의 모서리가 있습니다. 꼭지점 'e'와 'd'도 그들 사이에 두 개의 가장자리가 있습니다. 따라서 그것은 Multigraph입니다.
그래프의 차수 시퀀스
그래프에있는 모든 정점의 각도가 내림차순 또는 오름차순으로 배열 된 경우 얻은 시퀀스를 그래프의 각도 시퀀스라고합니다.
Example 1

| 꼭지점 | ㅏ | 비 | 씨 | 디 | 이자형 |
|---|---|---|---|---|---|
| 에 연결 | 기원전 | 기원 후 | 기원 후 | c, b, e | 디 |
| 정도 | 2 | 2 | 2 | 삼 | 1 |
위 그래프에서 정점 {d, a, b, c, e}의 경우 차수 시퀀스는 {3, 2, 2, 2, 1}입니다.
Example 2

| 꼭지점 | ㅏ | 비 | 씨 | 디 | 이자형 | 에프 |
|---|---|---|---|---|---|---|
| 에 연결 | 있다 | a, c | b, d | c, e | 기원 후 | - |
| 정도 | 2 | 2 | 2 | 2 | 2 | 0 |
위 그래프에서 정점 {a, b, c, d, e, f}의 경우 차수 시퀀스는 {2, 2, 2, 2, 2, 0}입니다.