그래프 이론-매칭
일치하는 그래프는 서로 인접한 가장자리가없는 그래프의 하위 그래프입니다. 간단히 말해서 두 모서리 사이에 공통 정점이 있어서는 안됩니다.
어울리는
'G'= (V, E)를 그래프라고합시다. 서브 그래프는 매칭 M (G)이라고합니다.if each vertex of G is incident with at most one edge in M즉,
deg (V) ≤ 1 ∀ V ∈ G
즉, 일치하는 그래프 M (G)에서 정점의 차수는 1 또는 0이어야하며, 여기서 가장자리는 그래프 G에서 입사해야합니다.
Notation − M (G)
Example
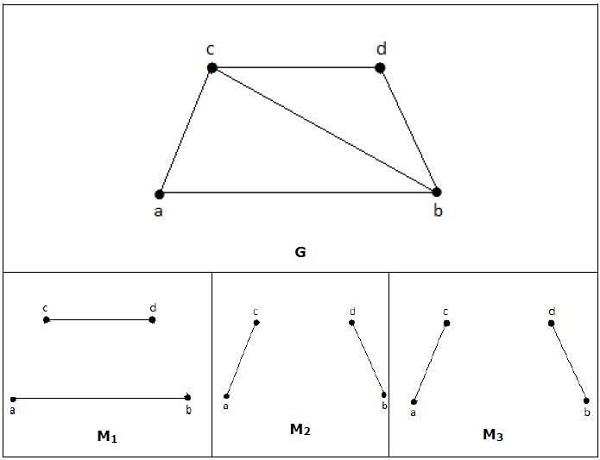

매칭에서
deg (V) = 1이면 (V)가 일치한다고합니다.
deg (V) = 0이면 (V)는 일치하지 않습니다.
일치에서 두 모서리가 인접하지 않습니다. 두 모서리가 인접하면 두 모서리를 연결하는 정점의 정도가 일치 규칙을 위반하는 정도가 2이기 때문입니다.
최대 매칭
그래프 'G'의 일치하는 M은 최대라고합니다. if no other edges of ‘G’ can be added to M.
Example

위 그래프에서 M1, M2, M3는 G의 최대 매칭입니다.
최대 매칭
최대 최대 일치라고도합니다. 최대 일치는 최대 모서리 수와의 최대 일치로 정의됩니다.
'G'의 최대 일치에있는 모서리 수를 matching number.
Example
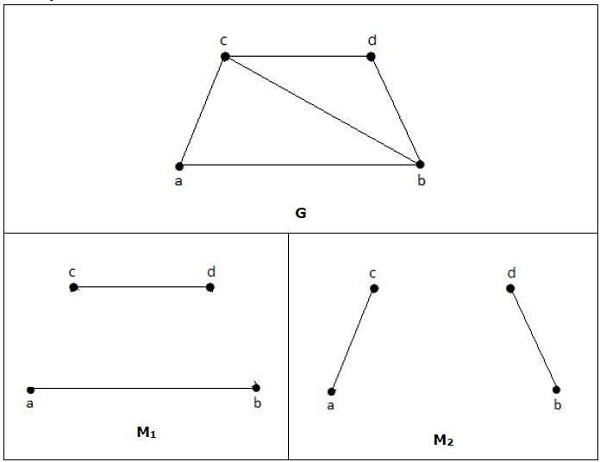
위의 예에서 주어진 그래프의 경우 M1과 M2는 'G'의 최대 일치 값이고 일치 개수는 2입니다. 따라서 그래프 G를 사용하면 최대 2 개의 모서리 만있는 부분 그래프 만 형성 할 수 있습니다. 따라서 일치하는 숫자는 2입니다.
완벽한 매칭
그래프 (G)의 일치 (M)는 그래프 g (G)의 모든 정점이 일치 (M)의 정확히 한 모서리에 입사하는 경우 완벽하게 일치한다고합니다.
deg (V) = 1∀V
하위 그래프의 각 꼭지점의 차수는 1이어야합니다.
Example
다음 그래프에서 M1과 M2는 G의 완벽한 매칭의 예입니다.
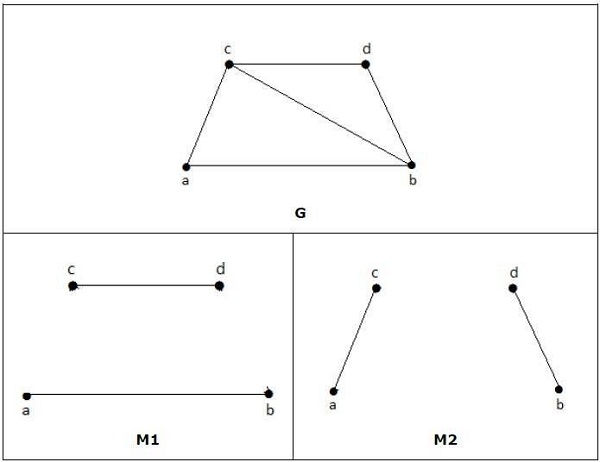
Note − 완벽하게 일치하는 그래프에 에지를 하나 더 추가 할 기회가 없기 때문에 그래프의 모든 완전 일치는 그래프의 최대 일치입니다.
그래프의 최대 일치가 완벽 할 필요는 없습니다. 그래프 'G'가 완벽하게 일치하면 정점 수 | V (G) | 짝수이다. 홀수이면 마지막 정점이 다른 정점과 쌍을 이루고 마지막으로 차수가 0 인 다른 정점과 쌍을 이룰 수없는 단일 정점이 남습니다. 완벽한 매칭 원칙을 분명히 위반합니다.
Example
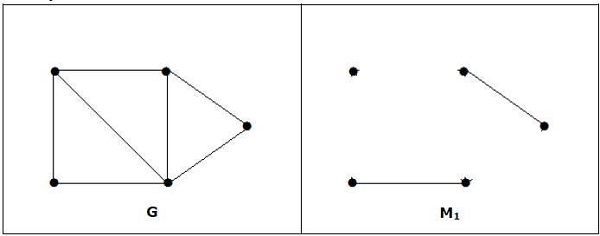
Note− 위 진술의 반대가 사실 일 필요는 없습니다. G에 정점이 짝수이면 M1이 완벽 할 필요는 없습니다.
Example
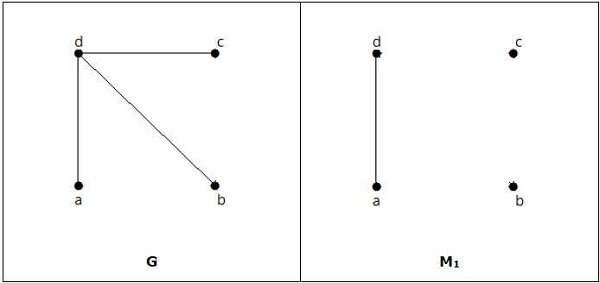
일치하지만 꼭지점이 짝수 인 경우에도 완벽한 일치는 아닙니다.