그래프 이론-예
이 장에서는 이전 장에서 이미 논의한 개념을 보여주는 몇 가지 표준 예제를 다룰 것입니다.
예 1
Find the number of spanning trees in the following graph.
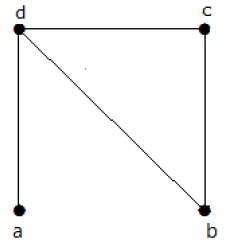
해결책
위 그래프에서 얻은 스패닝 트리의 개수는 3 개입니다.
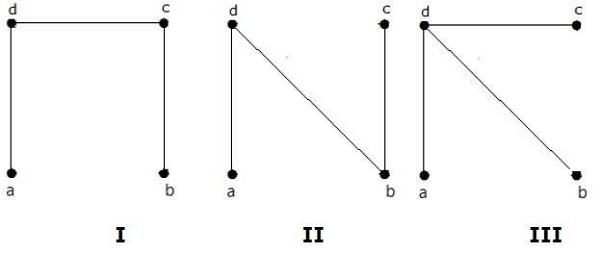
이 세 가지는 주어진 그래프에 대한 스패닝 트리입니다. 여기서 그래프 I와 II는 서로 동형입니다. 분명히 비 동형 스패닝 트리의 수는 2 개입니다.
예 2
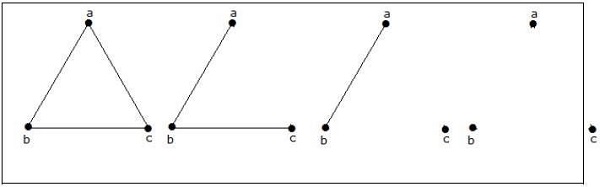
How many simple non-isomorphic graphs are possible with 3 vertices?
해결책
3 개의 꼭지점으로 가능한 4 개의 비 동형 그래프가 있습니다. 아래에 나와 있습니다.
예제 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
해결책
학위 정리의 합으로,
20 Σ i = 1 deg (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
오일러의 공식에 따르면
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
따라서 지역 수는 12 개입니다.
예 4
What is the chromatic number of complete graph Kn?
해결책
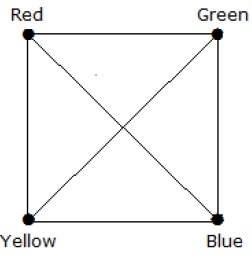
완전한 그래프에서 인접한 각 정점은 남아있는 (n-1) 정점입니다. 따라서 각 정점에는 새로운 색상이 필요합니다. 따라서, K 색 번호 N = N.
예 5
What is the matching number for the following graph?
해결책
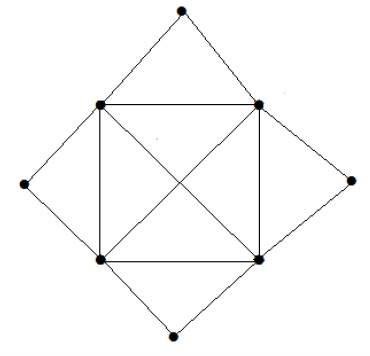
정점 수 = 9
8 개의 정점 만 일치시킬 수 있습니다.
일치하는 숫자는 4입니다.
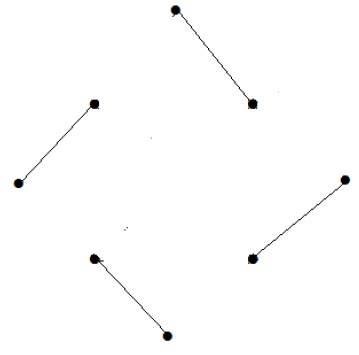
예제 6
What is the line covering number of for the following graph?
해결책
정점 수 = | V | = n = 7
라인 커버링 번호 = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
3 개의 모서리를 사용하여 모든 정점을 덮을 수 있습니다.
따라서 선을 덮는 숫자는 3입니다.