로그 및 안티 로그 증폭기
증폭과 함께 대수 및 반대 수 (지수)와 같은 수학적 연산을 수행하는 전자 회로를 다음과 같이 부릅니다. Logarithmic amplifier 과 Anti-Logarithmic amplifier 각기.
이 장에서는 다음에 대해 설명합니다. Logarithmic amplifier 과 Anti-Logarithmic amplifier상세히. 이러한 증폭기는 비선형 애플리케이션에 속합니다.
대수 증폭기
ㅏ logarithmic amplifier, 또는 log amplifier는 적용된 입력의 로그에 비례하는 출력을 생성하는 전자 회로입니다. 이 섹션에서는 연산 증폭기 기반 로그 증폭기에 대해 자세히 설명합니다.
연산 증폭기 기반 로그 증폭기는 출력에서 전압을 생성하며, 이는 반전 단자에 연결된 저항에 적용된 전압의 로그에 비례합니다. 그만큼circuit diagram 연산 증폭기 기반 로그 증폭기의 그림은 다음과 같습니다.
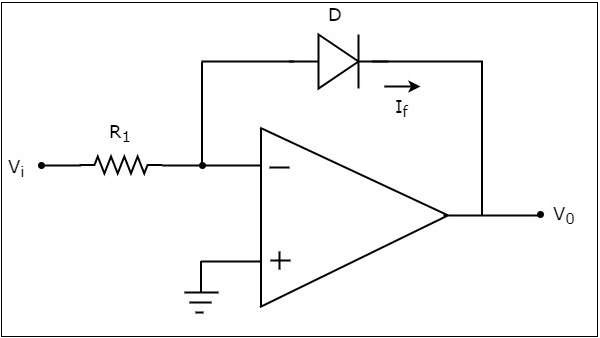
위의 회로에서 연산 증폭기의 비 반전 입력 단자는 접지에 연결됩니다. 즉, 연산 증폭기의 비 반전 입력 단자에 제로 볼트가 적용됩니다.
에 따르면 virtual short concept, 연산 증폭기의 반전 입력 단자의 전압은 비 반전 입력 단자의 전압과 동일합니다. 따라서 반전 입력 단자의 전압은 0V가됩니다.
그만큼 nodal equation 반전 입력 터미널의 노드에서-
$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$
$$ => I_ {f} = \ frac {V_i} {R_1} ...... 방정식 1 $$
다음은 equation for current 순방향 바이어스에있을 때 다이오드를 통해 흐르는-
$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... 방정식 2 $$
어디,
$ I_ {s} $는 다이오드의 포화 전류이고,
$ V_ {f} $는 순방향 바이어스 일 때 다이오드 양단의 전압 강하입니다.
$ V_ {T} $는 다이오드의 열 등가 전압입니다.
그만큼 KVL equation 연산 증폭기의 피드백 루프 주변은-
$$ 0-V_ {f} -V_ {0} = 0 $$
$$ => V_ {f} =-V_ {0} $$
방정식 2에서 $ V_ {f} $의 값을 대체하면 다음과 같이됩니다.
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} ...... 수식 3 $$
방정식 1과 방정식 3의 좌변 항이 동일한 지 확인하십시오. 따라서 다음과 같이 두 방정식의 우변 항을 동일시하십시오.
$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$
지원 natural logarithm 양쪽에서 우리는-
$$ In \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$
$$ V_ {0} =-{nV_T} In \ left (\ frac {V_i} {R_1I_s} \ right) $$
위 방정식에서 매개 변수 n, $ {V_T} $ 및 $ I_ {s} $는 상수입니다. 따라서 출력 전압 $ V_ {0} $는natural logarithm 저항 $ R_ {1} $의 고정 값에 대한 입력 전압 $ V_ {i} $.
따라서 위에서 논의한 연산 증폭기 기반 로그 증폭기 회로는 $ {R_1I_s} = 1V $ 일 때 입력 전압 $ {V_T} $의 자연 로그에 비례하는 출력을 생성합니다.
출력 전압 $ V_ {0} $에 negative sign, 이는 입력과 출력간에 180 0 위상차 가 있음을 나타냅니다 .
대수 방지 증폭기
안 anti-logarithmic amplifier, 또는 anti-log amplifier는 적용된 입력의 역대 수에 비례하는 출력을 생성하는 전자 회로입니다. 이 섹션에서는 연산 증폭기 기반 반 로그 증폭기에 대해 자세히 설명합니다.
연산 증폭기 기반의 대수 방지 증폭기는 출력에서 전압을 생성하며, 이는 반전 단자에 연결된 다이오드에 적용되는 전압의 대수에 비례합니다.
그만큼 circuit diagram 연산 증폭기 기반의 대수 방지 증폭기는 다음 그림에 나와 있습니다.

위의 회로에서 연산 증폭기의 비 반전 입력 단자는 접지에 연결됩니다. 이는 비 반전 입력 단자에 제로 볼트가 적용됨을 의미합니다.
에 따르면 virtual short concept, 연산 증폭기의 반전 입력 단자의 전압은 비 반전 입력 단자의 전압과 동일합니다. 따라서 반전 입력 단자의 전압은 0V가됩니다.
그만큼 nodal equation 반전 입력 터미널의 노드에서-
$$-I_ {f} + \ frac {0-V_0} {R_f} = 0 $$
$$ =>-\ frac {V_0} {R_f} = I_ {f} $$
$$ => V_ {0} =-R_ {f} I_ {f} ......... 방정식 4 $$
다이오드를 통해 흐르는 전류에 대한 방정식은 순방향 바이어스 일 때 다음과 같습니다.
$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)} $$
방정식 4에서 $ I_ {f} $의 값을 대체하면
$$ V_ {0} =-R_ {f} \ 왼쪽 \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} \ 오른쪽 \} $$
$$ V_ {0} =-R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} ...... 등식 5 $$
연산 증폭기의 반전 단자 입력 측의 KVL 방정식은 다음과 같습니다.
$$ V_ {i} -V_ {f} = 0 $$
$$ V_ {f} = V_ {i} $$
방정식 5의 값을 대입하면 다음과 같이됩니다.
$$ V_ {0} =-R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ right)}} $$
위의 방정식에서 매개 변수 n, $ {V_T} $ 및 $ I_ {s} $는 상수입니다. 따라서 출력 전압 $ {V_0} $은anti-natural logarithm 피드백 저항 $ {R_f} $의 고정 값에 대한 입력 전압 $ {V_i} $의 (지수).
따라서 위에서 논의한 연산 증폭기 기반 반 로그 증폭기 회로는 $ {R_fI_s} = 1V $ 일 때 입력 전압 $ {V_i} $의 반 자연 로그 (지수)에 비례하는 출력을 생성합니다. 출력 전압 $ {V_0} $에negative sign, 이는 입력과 출력간에 180 0 위상차 가 있음을 나타냅니다 .