Algorytm generowania koła

Rysowanie okręgu na ekranie jest trochę skomplikowane niż rysowanie linii. Istnieją dwa popularne algorytmy generowania okręgu -Bresenham’s Algorithm i Midpoint Circle Algorithm. Algorytmy te opierają się na idei wyznaczania kolejnych punktów potrzebnych do narysowania okręgu. Omówmy szczegółowo algorytmy -

Równanie koła to $ X ^ {2} + Y ^ {2} = r ^ {2}, $ gdzie r jest promieniem.

Algorytm Bresenham

Nie możemy wyświetlić ciągłego łuku na ekranie rastrowym. Zamiast tego musimy wybrać najbliższą pozycję piksela, aby zakończyć łuk.

Na poniższej ilustracji widać, że umieściliśmy piksel w miejscu (X, Y) i teraz musimy zdecydować, gdzie umieścić następny piksel - w N (X + 1, Y) lub w S (X + 1, Y-1).

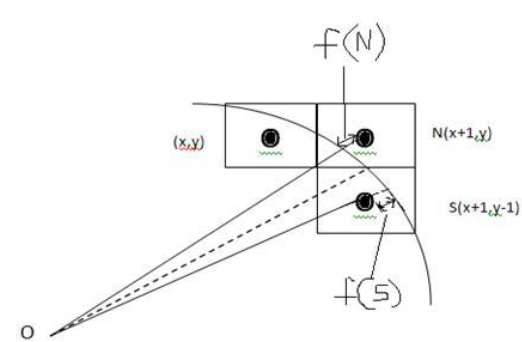
Decyduje o tym parametr decyzyjny d.

• Jeśli d <= 0, to N (X + 1, Y) należy wybrać jako następny piksel.
• Jeśli d> 0, to S (X + 1, Y-1) ma być wybrany jako następny piksel.

Algorytm

Step 1- Uzyskaj współrzędne środka okręgu i promienia i zapisz je odpowiednio w x, y i R. Ustaw P = 0 i Q = R.

Step 2 - Ustaw parametr decyzyjny D = 3 - 2R.

Step 3 - Powtórz krok 8, gdy P ≤ Q.

Step 4 - Call Draw Circle (X, Y, P, Q).

Step 5 - Zwiększ wartość P.

Step 6 - Jeśli D <0, to D = D + 4P + 6.

Step 7 - W przeciwnym razie ustaw R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Call Draw Circle (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Algorytm punktu środkowego

Step 1 - Promień wejściowy r i środek okręgu $ (x_ {c,} y_ {c}) $ i uzyskaj pierwszy punkt na obwodzie koła ze środkiem na początku jako

(x0, y0) = (0, r)

Step 2 - Obliczyć początkową wartość parametru decyzyjnego jako

$ P_ {0} $ = 5/4 - r (Zobacz poniższy opis w celu uproszczenia tego równania).

f(x, y) = x2 + y2 - r2 = 0

f(xi - 1/2 + e, yi + 1)
        = (xi - 1/2 + e)2 + (yi + 1)2 - r2 
        = (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
        = f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0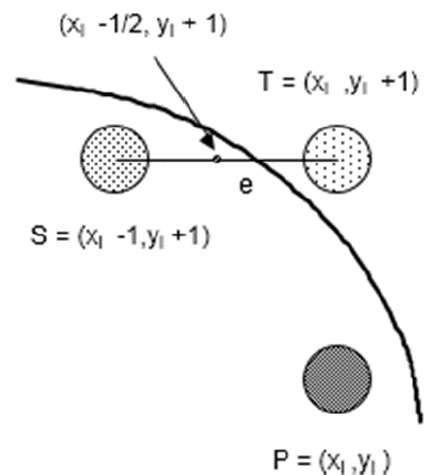

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,

If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1    = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
        = di - 2(xi - 1) + 2(yi + 1) + 1
        = di + 2(yi + 1 - xi + 1) + 1
		  
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
   di+1 = f(xi - 1/2, yi + 1 + 1)
       = di + 2yi+1 + 1
		  
The initial value of di is
   d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (xi - 1, yi + 1) is chosen then
   di+1 = di + -2xi+1 + 2yi+1 + 1
	
When point T = (xi, yi + 1) is chosen then
   di+1 = di + 2yi+1 + 1

Step 3 - Na każdej pozycji $ X_ {K} $ zaczynającej się od K = 0, przeprowadź następujący test -

If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
   PK+1 = PK + 2XK+1 + 1
Else
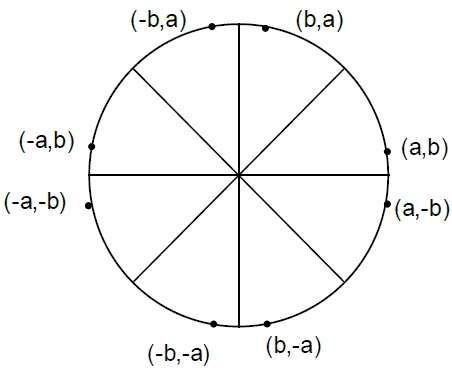
   PK+1 = PK + 2XK+1 + 1 – 2YK+1
	
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.

Step 4 - Określ punkty symetrii w pozostałych siedmiu oktantach.

Step 5 - Przenieś każdą obliczoną pozycję piksela (X, Y) na ścieżkę kołową wyśrodkowaną na $ (X_ {C,} Y_ {C}) $ i wykreśl wartości współrzędnych.

X = X + XC,   Y = Y + YC

Step 6 - Powtórz kroki od 3 do 5, aż X> = Y.