Powierzchnie grafiki komputerowej
Powierzchnie wieloboczne
Obiekty są reprezentowane jako zbiór powierzchni. Reprezentacja obiektów 3D jest podzielona na dwie kategorie.
Boundary Representations (B-reps) - Opisuje obiekt 3D jako zbiór powierzchni oddzielających wnętrze obiektu od otoczenia.
Space–partitioning representations - Służy do opisu właściwości wewnętrznych poprzez podział obszaru przestrzennego zawierającego obiekt na zbiór małych, nie nachodzących na siebie, ciągłych brył (zwykle kostek).
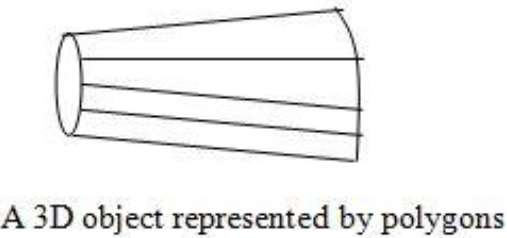
Najczęściej używaną reprezentacją obwiedni obiektu graficznego 3D jest zestaw wielokątów powierzchni, które otaczają wnętrze obiektu. Wiele systemów graficznych korzysta z tej metody. Zbiór wielokątów jest przechowywany dla opisu obiektu. Upraszcza to i przyspiesza renderowanie powierzchni i wyświetlanie obiektu, ponieważ wszystkie powierzchnie można opisać równaniami liniowymi.
Powierzchnie wielokątne są powszechne w aplikacjach do projektowania i modelowania brył, ponieważ ich wireframe displaymożna zrobić szybko, aby uzyskać ogólne wskazanie struktury powierzchni. Następnie tworzone są realistyczne sceny, interpolując wzory cieni na powierzchni wielokąta w celu oświetlenia.
Tabele wielokątne
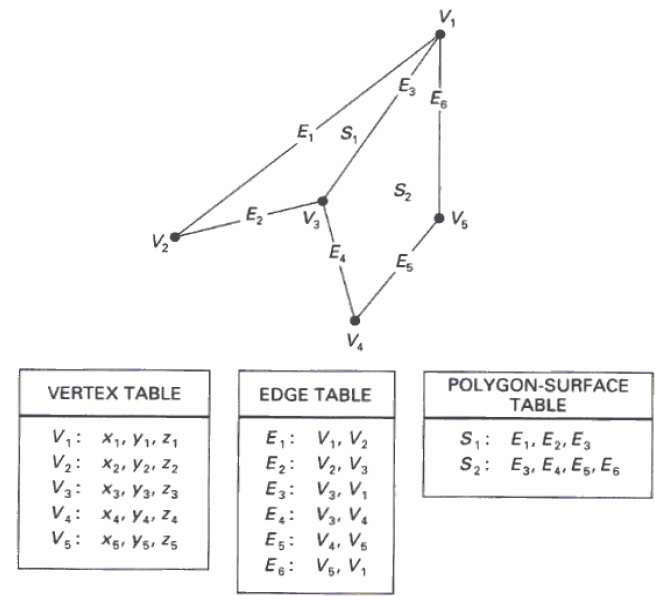
W tej metodzie powierzchnia jest określana przez zestaw współrzędnych wierzchołków i powiązanych atrybutów. Jak pokazano na poniższym rysunku, istnieje pięć wierzchołków, od v 1 do v 5 .
Każdy wierzchołek przechowuje informacje o współrzędnych x, y i z, które są reprezentowane w tabeli jako v 1 : x 1 , y 1 , z 1 .
Tabela Edge służy do przechowywania informacji o krawędziach wielokąta. Na poniższym rysunku krawędź E 1 leży między wierzchołkami v 1 i v 2, które w tabeli są reprezentowane jako E 1 : v 1 , v 2 .
Tabela powierzchni wieloboku przechowuje liczbę powierzchni obecnych w wielokącie. Na poniższym rysunku powierzchnia S 1 jest pokryta krawędziami E 1 , E 2 i E 3, które można przedstawić w tabeli powierzchni wieloboków jako S 1 : E 1 , E 2 i E 3 .
Równania płaszczyznowe
Równanie powierzchni płaskiej można wyrazić jako -
Ax + By + Cz + D = 0
Gdzie (x, y, z) to dowolny punkt na płaszczyźnie, a współczynniki A, B, C i D są stałymi opisującymi właściwości przestrzenne płaszczyzny. Możemy otrzymać wartości A, B, C i D, rozwiązując zestaw trzech równań płaszczyznowych, używając wartości współrzędnych dla trzech niekoliniowych punktów na płaszczyźnie. Załóżmy, że trzy wierzchołki płaszczyzny to (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) i (x 3 , y 3 , z 3 ).
Rozwiążmy następujące równania równoczesne dla stosunków A / D, B / D i C / D. Otrzymasz wartości A, B, C i D.
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
Aby otrzymać powyższe równania w formie wyznacznika, zastosuj regułę Cramera do powyższych równań.
$ A = \ begin {bmatrix} 1 & y_ {1} & z_ {1} \\ 1 & y_ {2} & z_ {2} \\ 1 & y_ {3} & z_ {3} \ end {bmatrix} B = \ begin {bmatrix} x_ {1} & 1 & z_ {1} \\ x_ {2} & 1 & z_ {2} \\ x_ {3} & 1 & z_ {3} \ end {bmatrix} C = \ begin {bmatrix} x_ {1} & y_ {1} & 1 \\ x_ {2} & y_ {2} & 1 \\ x_ {3} & y_ {3} & 1 \ end {bmatrix} D = - \ begin {bmatrix} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \ end {bmatrix } $
Dla dowolnego punktu (x, y, z) z parametrami A, B, C i D możemy powiedzieć, że -
Ax + By + Cz + D ≠ 0 oznacza, że punkt nie znajduje się na płaszczyźnie.
Ax + By + Cz + D <0 oznacza, że punkt znajduje się wewnątrz powierzchni.
Ax + By + Cz + D> 0 oznacza, że punkt znajduje się poza powierzchnią.
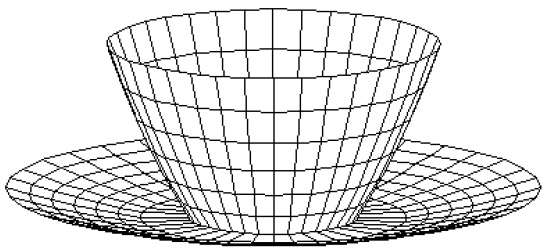
Siatki wielokątne
Powierzchnie i bryły 3D można aproksymować za pomocą zestawu elementów wielokątnych i liniowych. Takie powierzchnie nazywane sąpolygonal meshes. W siatce wielokątnej każda krawędź jest wspólna dla co najwyżej dwóch wielokątów. Zestaw wielokątów lub ścian razem tworzy „skórę” obiektu.
Ta metoda może być używana do reprezentowania szerokiej klasy brył / powierzchni w grafice. Siatkę wielokątną można renderować za pomocą algorytmów usuwania ukrytej powierzchni. Siatkę wielokątną można przedstawić na trzy sposoby -
- Jawna reprezentacja
- Wskaźniki do listy wierzchołków
- Wskaźniki do listy krawędzi
Zalety
- Może być używany do modelowania prawie każdego obiektu.
- Można je łatwo przedstawić jako zbiór wierzchołków.
- Łatwo je przekształcić.
- Można je łatwo narysować na ekranie komputera.
Niedogodności
- Zakrzywione powierzchnie można opisać tylko w przybliżeniu.
- Trudno jest symulować niektóre rodzaje obiektów, takie jak włosy lub ciecz.