Algorytm wypełniania wielokątów
Wielokąt to uporządkowana lista wierzchołków, jak pokazano na poniższym rysunku. Aby wypełnić wielokąty określonymi kolorami, musisz określić piksele mieszczące się na granicy wielokąta i te, które mieszczą się wewnątrz wielokąta. W tym rozdziale zobaczymy, jak wypełnić wielokąty różnymi technikami.

Algorytm skanowania linii
Ten algorytm działa poprzez przecięcie linii skanowania z krawędziami wielokątów i wypełnienie wielokąta między parami przecięć. Poniższe kroki przedstawiają sposób działania tego algorytmu.
Step 1 - Znajdź Ymin i Ymax z podanego wielokąta.
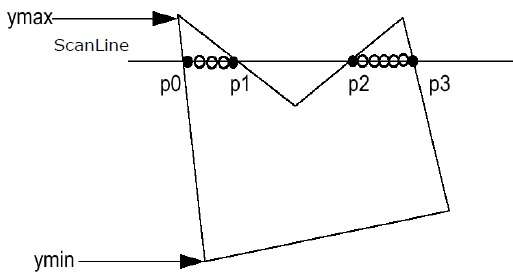
Step 2- ScanLine przecina się z każdą krawędzią wielokąta od Ymin do Ymax. Nazwij każdy punkt przecięcia wielokąta. Zgodnie z powyższym rysunkiem są one nazwane p0, p1, p2, p3.
Step 3 - Uporządkuj punkt przecięcia w kolejności rosnącej współrzędnej X, tj. (P0, p1), (p1, p2) i (p2, p3).
Step 4 - Wypełnij wszystkie te pary współrzędnych, które są wewnątrz wielokątów i zignoruj alternatywne pary.
Algorytm wypełniania powodzi
Czasami spotykamy obiekt, w którym chcemy wypełnić obszar i jego granicę różnymi kolorami. Możemy pomalować takie obiekty na określony kolor wnętrza, zamiast szukać określonego koloru granicy, jak w algorytmie wypełniania granic.
Zamiast polegać na granicy obiektu, opiera się na kolorze wypełnienia. Innymi słowy, zastępuje kolor wnętrza obiektu kolorem wypełnienia. Gdy nie ma już pikseli w oryginalnym kolorze wnętrza, algorytm jest zakończony.
Po raz kolejny ten algorytm opiera się na metodzie czterech połączeń lub ośmiu połączeń wypełniania pikseli. Ale zamiast szukać koloru granicznego, szuka wszystkich sąsiednich pikseli, które są częścią wnętrza.
Algorytm wypełnienia granicy
Algorytm wypełniania granic działa jak jego nazwa. Ten algorytm wybiera punkt wewnątrz obiektu i zaczyna wypełniać, dopóki nie dotknie granicy obiektu. Aby algorytm zadziałał, kolor granicy i kolor, który wypełniamy, powinny być inne.
W tym algorytmie zakładamy, że kolor granicy jest taki sam dla całego obiektu. Algorytm wypełniania granic można zaimplementować za pomocą 4 połączonych pikseli lub 8 połączonych pikseli.
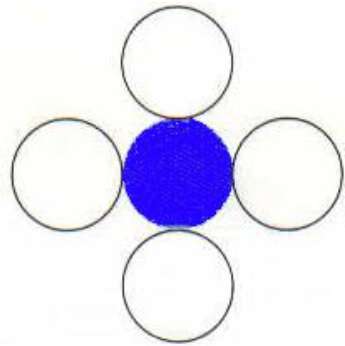
4-połączony wielokąt
W tej technice używa się 4 połączonych pikseli, jak pokazano na rysunku. Umieszczamy piksele powyżej, poniżej, po prawej i po lewej stronie bieżących pikseli i ten proces będzie kontynuowany, dopóki nie znajdziemy granicy o innym kolorze.
Algorytm
Step 1 - Zainicjuj wartość punktu początkowego (seedx, seedy), fcolor i dcol.
Step 2 - Zdefiniuj wartości graniczne wielokąta.
Step 3 - Sprawdź, czy bieżący punkt początkowy ma domyślny kolor, a następnie powtórz kroki 4 i 5, aż osiągną piksele graniczne.
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - Zmień domyślny kolor na kolor wypełnienia w punkcie początkowym.
setPixel(seedx, seedy, fcol)Step 5 - Rekurencyjnie postępuj zgodnie z procedurą z czterema punktami sąsiedztwa.
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - Wyjdź
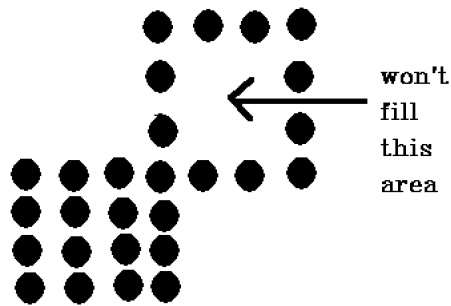
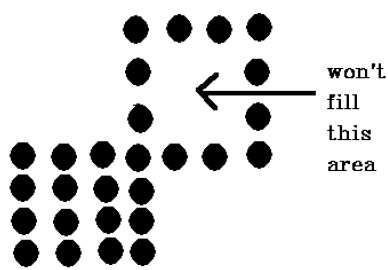
Jest problem z tą techniką. Rozważmy przypadek pokazany poniżej, w którym próbowaliśmy wypełnić cały region. Tutaj obraz jest wypełniony tylko częściowo. W takich przypadkach nie można użyć techniki 4 połączonych pikseli.
8-połączony wielokąt
W tej technice używa się 8 połączonych pikseli, jak pokazano na rysunku. Umieszczamy piksele powyżej, poniżej, prawej i lewej strony bieżących pikseli, tak jak robiliśmy to w technice 4-połączonej.
Oprócz tego umieszczamy piksele na przekątnych, aby pokryć cały obszar bieżącego piksela. Ten proces będzie trwał, dopóki nie znajdziemy granicy o innym kolorze.

Algorytm
Step 1 - Zainicjuj wartość punktu początkowego (seedx, seedy), fcolor i dcol.
Step 2 - Zdefiniuj wartości graniczne wielokąta.
Step 3 - Sprawdź, czy bieżący punkt początkowy ma domyślny kolor, a następnie powtórz kroki 4 i 5, aż do osiągnięcia pikseli granicznych
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - Zmień domyślny kolor na kolor wypełnienia w punkcie początkowym.
setPixel(seedx, seedy, fcol)Step 5 - Rekurencyjnie postępuj zgodnie z procedurą z czterema punktami sąsiedztwa
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - Wyjdź
Technika 4-połączonych pikseli nie wypełniła obszaru, jak zaznaczono na poniższym rysunku, co nie nastąpi w przypadku techniki 8-połączonych.
Test wewnątrz-na zewnątrz
Ta metoda jest również znana jako counting number method. Podczas wypełniania obiektu często musimy określić, czy dany punkt znajduje się wewnątrz obiektu, czy na zewnątrz. Istnieją dwie metody, za pomocą których możemy określić, czy dany punkt znajduje się wewnątrz obiektu, czy na zewnątrz.
- Zasada nieparzysta-parzysta
- Niezerowa reguła liczby uzwojeń
Zasada nieparzysta-parzysta
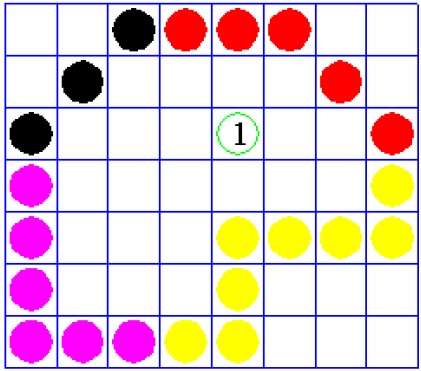
W tej technice policzymy przejście krawędzi wzdłuż linii od dowolnego punktu (x, y) do nieskończoności. Jeśli liczba interakcji jest nieparzysta, to punkt (x, y) jest punktem wewnętrznym; a jeśli liczba interakcji jest parzysta, to punkt (x, y) jest punktem zewnętrznym. Poniższy przykład przedstawia tę koncepcję.
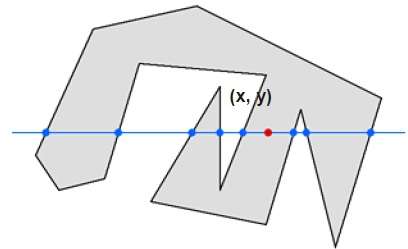
Z powyższego rysunku widzimy, że z punktu (x, y) liczba punktów interakcji po lewej stronie wynosi 5, a po prawej 3. Z obu końców liczba punktów interakcji jest nieparzysta, więc punkt jest uwzględniany w obiekcie.
Niezerowa reguła liczby uzwojeń
Ta metoda jest również używana w przypadku prostych wielokątów, aby sprawdzić, czy dany punkt jest wewnętrzny, czy nie. Można to po prostu zrozumieć za pomocą szpilki i gumki. Zamocuj szpilkę na jednej z krawędzi wielokąta i zawiąż w nim gumkę, a następnie rozciągnij gumkę wzdłuż krawędzi wielokąta.
Kiedy wszystkie krawędzie wielokąta są zakryte gumką, sprawdź szpilkę, która została zamocowana w punkcie, który ma być testowany. Jeśli znajdziemy przynajmniej jeden wiatr w tym punkcie, rozważmy go wewnątrz wielokąta, w przeciwnym razie możemy powiedzieć, że punkt nie znajduje się wewnątrz wielokąta.
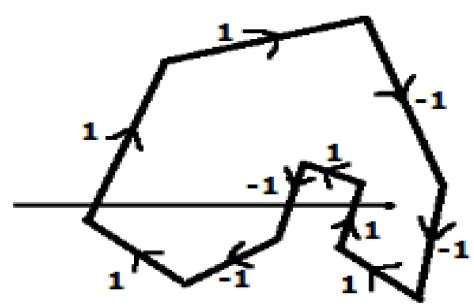
W innej alternatywnej metodzie podaj wskazówki dla wszystkich krawędzi wielokąta. Narysuj linię skanowania od badanego punktu w skrajną lewą stronę kierunku X.
Podaj wartość 1 wszystkim krawędziom, które idą w górę, a wszystkim innym -1 jako wartości kierunku.
Sprawdź wartości kierunku krawędzi, od których przechodzi linia skanowania i zsumuj je.
Jeśli całkowita suma wartości tego kierunku jest różna od zera, to testowany punkt jest interior point, w przeciwnym razie jest to plik exterior point.
Na powyższym rysunku sumujemy wartości kierunku, z którego przechodzi linia skanowania, a następnie suma wynosi 1 - 1 + 1 = 1; która jest różna od zera. Mówi się więc, że punkt jest punktem wewnętrznym.