Krzywe grafiki komputerowej

W grafice komputerowej często musimy rysować na ekranie różne typy obiektów. Obiekty nie są przez cały czas płaskie i trzeba wiele razy rysować krzywe, aby narysować obiekt.

Rodzaje krzywych

Krzywa to nieskończenie duży zbiór punktów. Każdy punkt ma dwóch sąsiadów z wyjątkiem punktów końcowych. Krzywe można ogólnie podzielić na trzy kategorie -explicit, implicit, i parametric curves.

Ukryte krzywe

Niejawne reprezentacje krzywych definiują zestaw punktów na krzywej, stosując procedurę, która może przetestować, czy punkt na krzywej. Zwykle ukryta krzywa jest definiowana przez niejawną funkcję postaci -

f (x, y) = 0

Może przedstawiać krzywe wielowartościowe (wiele wartości y dla wartości x). Typowym przykładem jest okrąg, którego niejawna reprezentacja to

x² + y² - R² = 0

Wyraźne krzywe

Funkcję matematyczną y = f (x) można przedstawić jako krzywą. Taka funkcja jest jawną reprezentacją krzywej. Jawna reprezentacja nie jest ogólna, ponieważ nie może przedstawiać pionowych linii i jest również jednowartościowa. Dla każdej wartości x funkcja oblicza zwykle tylko jedną wartość y.

Krzywe parametryczne

Krzywe mające formę parametryczną nazywane są krzywymi parametrycznymi. Jawne i niejawne reprezentacje krzywych mogą być używane tylko wtedy, gdy funkcja jest znana. W praktyce wykorzystuje się krzywe parametryczne. Dwuwymiarowa krzywa parametryczna ma następującą postać -

P (t) = f (t), g (t) lub P (t) = x (t), y (t)

Funkcje f i g stają się współrzędnymi (x, y) dowolnego punktu na krzywej, a punkty są uzyskiwane, gdy parametr t zmienia się w pewnym przedziale [a, b], zwykle [0, 1].

Krzywe Beziera

Krzywa Beziera została odkryta przez francuskiego inżyniera Pierre Bézier. Te krzywe można generować pod kontrolą innych punktów. Przybliżone styczne przy użyciu punktów kontrolnych są używane do generowania łuku. Krzywą Beziera można przedstawić matematycznie jako -

$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$

Gdzie $ p_ {i} $ jest zbiorem punktów, a $ {B_ {i} ^ {n}} (t) $ reprezentuje wielomiany Bernsteina, które są podane przez -

$$ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i} $$

Gdzie n jest stopniem wielomianu, i jest indeksem, a t jest zmienną.

Najprostszą krzywą Béziera jest linia prosta od punktu $ P_ {0} $ do $ P_ {1} $. Kwadratową krzywą Beziera wyznaczają trzy punkty kontrolne. Sześcienna krzywa Beziera jest wyznaczona przez cztery punkty kontrolne.

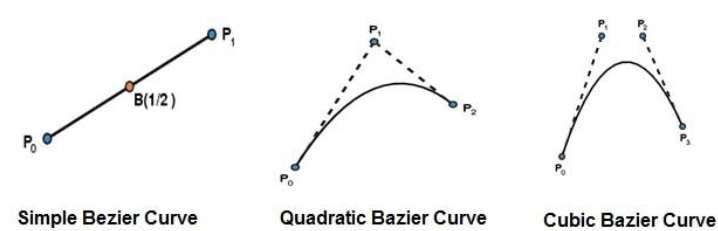
Właściwości krzywych Beziera

Krzywe Beziera mają następujące właściwości -

Zwykle mają kształt wielokąta kontrolnego, który składa się z segmentów łączących punkty kontrolne.
Zawsze przechodzą przez pierwszy i ostatni punkt kontrolny.
Są zawarte w wypukłym kadłubie ich definiujących punktów kontrolnych.
Stopień wielomianu definiującego segment krzywej jest o jeden mniejszy od liczby definiującego punktu wielokąta. Dlatego dla 4 punktów kontrolnych stopień wielomianu wynosi 3, czyli wielomian sześcienny.
Krzywa Beziera na ogół podąża za kształtem definiującego wielokąta.
Kierunek wektora stycznego w punktach końcowych jest taki sam, jak wektora określonego przez pierwszy i ostatni odcinek.
Wypukła właściwość kadłuba dla krzywej Beziera zapewnia, że wielomian płynnie podąża za punktami kontrolnymi.
Żadna prosta linia nie przecina krzywej Beziera więcej razy, niż przecina jej wielokąt kontrolny.
Są niezmienne przy transformacji afinicznej.
Krzywe Beziera zapewniają kontrolę globalną, co oznacza, że przesunięcie punktu kontrolnego zmienia kształt całej krzywej.
Dana krzywa Beziera może zostać podzielona w punkcie t = t0 na dwa segmenty Beziera, które łączą się ze sobą w punkcie odpowiadającym wartości parametru t = t0.

Krzywe typu B-Spline

Krzywa Beziera utworzona przez funkcję bazową Bernsteina ma ograniczoną elastyczność.

Po pierwsze, liczba określonych wierzchołków wielokąta ustala kolejność wynikowego wielomianu, który definiuje krzywą.
Drugą cechą ograniczającą jest to, że wartość funkcji mieszania jest różna od zera dla wszystkich wartości parametrów na całej krzywej.

Baza B-splajnu zawiera bazę Bernsteina jako przypadek specjalny. Podstawa B-splajnu nie jest globalna.

Krzywa B-splajn jest zdefiniowana jako liniowa kombinacja punktów kontrolnych Pi i funkcji bazowej B-spline $ N_ {i,} $ k (t) dana przez

$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \: \ epsilon \: [ tk-1, tn + 1] $

Gdzie,

{$ p_ {i} $: i = 0, 1, 2… .n} to punkty kontrolne
k jest rzędem segmentów wielomianów krzywej B-splajn. Rząd k oznacza, że krzywa składa się z odcinków wielomianowych odcinków stopnia k - 1,
$ N_ {i, k} (t) $ są „znormalizowanymi funkcjami mieszania B-splajn”. Opisuje je rząd k oraz nie malejąca sekwencja liczb rzeczywistych, zwykle nazywana „sekwencją węzłów”.

$$ {t_ {i}: i = 0, ... n + K} $$

Funkcje N _i , k są opisane następująco -

$$ N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 , & W przeciwnym razie \ end {matrix} \ right. $$

a jeśli k> 1,

$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t) $$

$$ t \: \ epsilon \: [t_ {k-1}, t_ {n + 1}) $$

Właściwości krzywej B-splajn

Krzywe B-splajn mają następujące właściwości -

Suma funkcji bazowych B-splajn dla dowolnej wartości parametru wynosi 1.
Każda funkcja bazowa jest dodatnia lub zerowa dla wszystkich wartości parametrów.
Każda funkcja bazowa ma dokładnie jedną wartość maksymalną, z wyjątkiem k = 1.
Maksymalna kolejność krzywej jest równa liczbie wierzchołków definiującego wielokąta.
Stopień wielomianu B-splajn jest niezależny od liczby wierzchołków wielokąta definiującego.
B-splajn umożliwia lokalną kontrolę nad powierzchnią krzywej, ponieważ każdy wierzchołek wpływa na kształt krzywej tylko w zakresie wartości parametrów, w przypadku których skojarzona z nim funkcja bazowa jest różna od zera.
Krzywa wykazuje właściwość zmniejszania zmienności.
Krzywa na ogół ma kształt definiującego wielokąta.
Dowolną transformację afiniczną można zastosować do krzywej, stosując ją do wierzchołków definiującego wielokąta.
Linia krzywej wewnątrz wypukłego kadłuba definiującego go wielokąta.