Algorytm generacji linii

Linia łączy dwa punkty. To podstawowy element grafiki. Aby narysować linię, potrzebujesz dwóch punktów, między którymi możesz narysować linię. W poniższych trzech algorytmach jeden punkt linii określamy jako $ X_ {0}, Y_ {0} $, a do drugiego punktu linii jako $ X_ {1}, Y_ {1} $.

Algorytm DDA

Algorytm Digital Differential Analyzer (DDA) to prosty algorytm generowania linii, który jest tutaj wyjaśniony krok po kroku.

Step 1 - Uzyskaj dane wejściowe dwóch punktów końcowych $ (X_ {0}, Y_ {0}) $ i $ (X_ {1}, Y_ {1}) $.

Step 2 - Oblicz różnicę między dwoma punktami końcowymi.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3- W oparciu o obliczoną różnicę w kroku 2, musisz określić liczbę kroków do umieszczenia piksela. Jeśli dx> dy, potrzebujesz więcej kroków we współrzędnej x; w przeciwnym razie we współrzędnej y.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 - Oblicz przyrost we współrzędnej x i współrzędnej y.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 - Umieść piksel, odpowiednio zwiększając współrzędne xiy, i zakończ rysowanie linii.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham's Line Generation

Algorytm Bresenham to kolejny algorytm konwersji przyrostowej skanowania. Dużą zaletą tego algorytmu jest to, że używa tylko obliczeń całkowitych. Poruszając się po osi X w jednostkowych odstępach i na każdym kroku wybieraj jedną z dwóch różnych współrzędnych y.

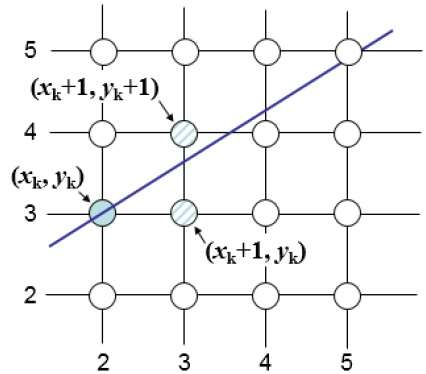
Na przykład, jak pokazano na poniższej ilustracji, z pozycji (2, 3) należy wybrać pomiędzy (3, 3) a (3, 4). Chciałbyś, aby punkt był bliżej oryginalnej linii.

W pozycji próbki $ X_ {k} + 1, $ pionowe separacje od linii matematycznej są oznaczone jako $ d_ {górne} $ i $ d_ {dolne} $.

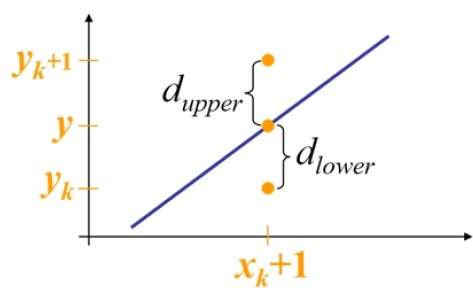
Na powyższej ilustracji współrzędna y na linii matematycznej przy $ x_ {k} + 1 $ wynosi -

Y = m ($ X_ {k} $ + 1) + b

Zatem $ d_ {upper} $ i $ d_ {lower} $ są podane w następujący sposób -

$$ d_ {lower} = y-y_ {k} $$

$$ = m (X_ {k} + 1) + b - Y_ {k} $$

$$ d_ {upper} = (y_ {k} + 1) - y $$

$ = Y_ {k} + 1 - m (X_ {k} + 1) - b $

Możesz ich użyć, aby podjąć prostą decyzję o tym, który piksel znajduje się bliżej linii matematycznej. Ta prosta decyzja opiera się na różnicy między dwoma położeniami pikseli.

$$ d_ {dolny} - d_ {górny} = 2m (x_ {k} + 1) - 2y_ {k} + 2b - 1 $$

Podstawmy m przez dy / dx, gdzie dx i dy są różnicami między punktami końcowymi.

$$ dx (d_ {dolny} - d_ {górny}) = dx (2 \ frac {\ mathrm {d} y} {\ mathrm {d} x} (x_ {k} + 1) - 2y_ {k} + 2b - 1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + 2dy + 2dx (2b-1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

Zatem parametr decyzyjny $ P_ {k} $ dla k- tego kroku wzdłuż linii jest określony wzorem -

$$ p_ {k} = dx (d_ {dolny} - d_ {górny}) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

Znak parametru decyzyjnego $ P_ {k} $ jest taki sam jak znak $ d_ {dolny} - d_ {górny} $.

Jeśli $ p_ {k} $ jest ujemne, wybierz dolny piksel, w przeciwnym razie wybierz górny piksel.

Pamiętaj, że zmiany współrzędnych następują wzdłuż osi x w krokach jednostkowych, więc możesz zrobić wszystko z obliczeniami całkowitymi. W kroku k + 1 parametr decyzyjny jest podawany jako -

$$ p_ {k +1} = 2dy.x_ {k + 1} - 2dx.y_ {k + 1} + C $$

Odejmując $ p_ {k} $ od tego otrzymujemy -

$$ p_ {k + 1} - p_ {k} = 2dy (x_ {k + 1} - x_ {k}) - 2dx (y_ {k + 1} - y_ {k}) $$

Ale $ x_ {k + 1} $ to to samo, co $ (xk) + 1 $. Więc -

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx (y_ {k + 1} - y_ {k}) $$

Gdzie $ Y_ {k + 1} - Y_ {k} $ wynosi 0 lub 1 w zależności od znaku $ P_ {k} $.

Pierwszy parametr decyzyjny $ p_ {0} $ jest oceniany na $ (x_ {0}, y_ {0}) $ jest podawany jako -

$$ p_ {0} = 2dy - dx $$

Mając na uwadze wszystkie powyższe punkty i obliczenia, oto algorytm Bresenham dla nachylenia m <1 -

Step 1 - Wprowadź dwa punkty końcowe linii, przechowując lewy punkt końcowy w $ (x_ {0}, y_ {0}) $.

Step 2 - Wykreśl punkt $ (x_ {0}, y_ {0}) $.

Step 3 - Oblicz stałe dx, dy, 2dy i (2dy - 2dx) i uzyskaj pierwszą wartość parametru decyzyjnego jako -

$$ p_ {0} = 2dy - dx $$

Step 4 - Przy każdym $ X_ {k} $ wzdłuż linii, zaczynając od k = 0, wykonaj następujący test -

Jeśli $ p_ {k} $ <0, następnym punktem na wykresie jest $ (x_ {k} +1, y_ {k}) $ i

$$ p_ {k + 1} = p_ {k} + 2dy $$ W przeciwnym razie

$$ (x_ {k}, y_ {k} +1) $$

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx $$

Step 5 - Powtórz krok 4 (dx - 1) razy.

Dla m> 1, dowiedz się, czy musisz zwiększać x, zwiększając jednocześnie y za każdym razem.

Po rozwiązaniu równanie dla parametru decyzyjnego $ P_ {k} $ będzie bardzo podobne, tylko x i y w równaniu zostaną zamienione.

Algorytm punktu środkowego

Algorytm punktu środkowego zawdzięczamy Bresenhamowi, który został zmodyfikowany przez Pittewaya i Van Akena. Załóżmy, że punkt P został już umieszczony we współrzędnej (x, y), a nachylenie linii wynosi 0 ≤ k ≤ 1, jak pokazano na poniższej ilustracji.

Teraz musisz zdecydować, czy umieścić następny punkt na E, czy N. Można to wybrać, identyfikując punkt przecięcia Q najbliższy punktowi N lub E. Jeśli punkt przecięcia Q jest najbliżej punktu N, wówczas N jest uważane za następny punkt; inaczej E.

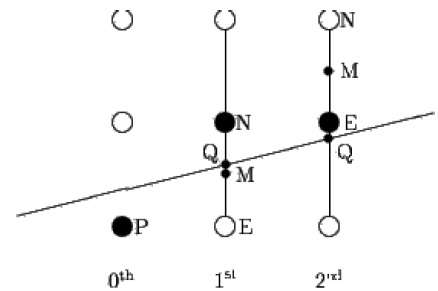
Aby to ustalić, najpierw oblicz punkt środkowy M (x + 1, y + ½). Jeśli punkt przecięcia Q prostej z pionową linią łączącą E i N znajduje się poniżej M, to E jako następny punkt; w przeciwnym razie weź N jako następny punkt.

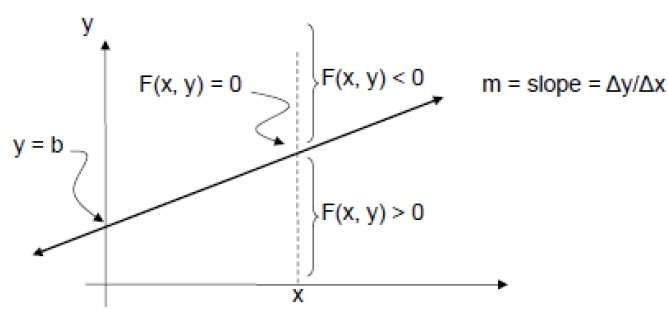
Aby to sprawdzić, musimy rozważyć niejawne równanie -

F (x, y) = mx + b - y

Dla dodatniego m przy dowolnym danym X,

Jeśli y jest na linii, to F (x, y) = 0
Jeśli y jest powyżej linii, to F (x, y) <0
Jeśli y jest poniżej linii, to F (x, y)> 0