Logika rozmyta - teoria mnogości
Zbiory rozmyte można uznać za rozszerzenie i rażące uproszczenie zbiorów klasycznych. Najlepiej można to zrozumieć w kontekście członkostwa w zestawie. Zasadniczo umożliwia częściowe członkostwo, co oznacza, że zawiera elementy, które mają różne stopnie członkostwa w zbiorze. Na tej podstawie możemy zrozumieć różnicę między zestawem klasycznym a rozmytym. Zbiór klasyczny zawiera elementy spełniające precyzyjne właściwości przynależności, natomiast zbiór rozmyty zawiera elementy spełniające nieprecyzyjne właściwości przynależności.

Pojęcie matematyczne
Rozmyty zbiór $ \ widetilde {A} $ we wszechświecie informacji $ U $ można zdefiniować jako zbiór uporządkowanych par i można go matematycznie przedstawić jako -
$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ in U \ right \} $$
Tutaj $ \ mu _ {\ widetilde {A}} \ left (y \ right) $ = stopień członkostwa $ y $ in \ widetilde {A}, przyjmuje wartości z zakresu od 0 do 1, czyli $ \ mu _ {\ widetilde {A}} (y) \ in \ left [0,1 \ right] $.
Reprezentacja zbioru rozmytego
Rozważmy teraz dwa przypadki wszechświata informacji i zrozummy, jak można przedstawić zbiór rozmyty.
Przypadek 1
Kiedy wszechświat informacji $ U $ jest dyskretny i skończony -
$$ \ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left (y_1 \ right)} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_2 \ right)} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_3 \ right)} {y_3} + ... \ right \} $$
$ = \ left \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ left (y_i \ right)} {y_i} \ right \} $
Przypadek 2
Kiedy wszechświat informacji $ U $ jest ciągły i nieskończony -
$$ \ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left (y \ right)} {y} \ right \} $$
W powyższej reprezentacji symbol sumowania reprezentuje zbiór każdego elementu.
Operacje na zbiorach rozmytych
Mając dwa zbiory rozmyte $ \ widetilde {A} $ i $ \ widetilde {B} $, wszechświat informacji $ U $ i element wszechświata, poniższe relacje wyrażają sumę, przecięcie i uzupełnienie operacji na zbiorach rozmytych.
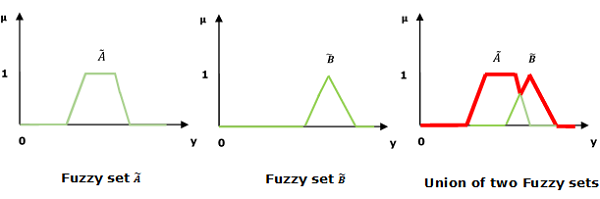
Union / Fuzzy „OR”
Rozważmy następującą reprezentację, aby zrozumieć, w jaki sposób Union/Fuzzy ‘OR’ relacja działa -
$$ \ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$
Tutaj ∨ oznacza operację „max”.
Przecięcie / rozmyte „AND”
Rozważmy następującą reprezentację, aby zrozumieć, w jaki sposób Intersection/Fuzzy ‘AND’ relacja działa -
$$ \ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \ quad \ forall y \ in U $$
Tutaj ∧ reprezentuje operację „min”.

Dopełnienie / rozmyte „NIE”
Rozważmy następującą reprezentację, aby zrozumieć, w jaki sposób Complement/Fuzzy ‘NOT’ relacja działa -
$$ \ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ left (y \ right) \ quad y \ in U $$

Właściwości zbiorów rozmytych
Omówmy różne właściwości zbiorów rozmytych.
Właściwość przemienna
Mając dwa rozmyte zbiory $ \ widetilde {A} $ i $ \ widetilde {B} $, ta właściwość określa -
$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $$
Łączność
Mając trzy rozmyte zbiory $ \ widetilde {A} $, $ \ widetilde {B} $ i $ \ widetilde {C} $, ta właściwość określa -
$$ (\ widetilde {A} \ cup \ left \ widetilde {B}) \ cup \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right) \ cup \ widetilde {C}) $$
$$ (\ widetilde {A} \ cap \ left \ widetilde {B}) \ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup (\ widetilde {B} \ right \ cap \ widetilde { C}) $$
Własność dystrybucyjna
Mając trzy rozmyte zbiory $ \ widetilde {A} $, $ \ widetilde {B} $ i $ \ widetilde {C} $, ta właściwość określa -
$$ \ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cap \ left (\ widetilde {A} \ cup \ widetilde {C} \ right) $$
$$ \ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde {B} \ right) \ cup \ left (\ widetilde {A} \ cap \ widetilde {C} \ right) $$
Właściwość Idempotencji
Dla każdego rozmytego zestawu $ \ widetilde {A} $ ta właściwość określa -
$$ \ widetilde {A} \ cup \ widetilde {A} = \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ widetilde {A} = \ widetilde {A} $$
Własność tożsamości
Dla zbioru rozmytego $ \ widetilde {A} $ i zbioru uniwersalnego $ U $, ta właściwość określa -
$$ \ widetilde {A} \ cup \ varphi = \ widetilde {A} $$
$$ \ widetilde {A} \ cap U = \ widetilde {A} $$
$$ \ widetilde {A} \ cap \ varphi = \ varphi $$
$$ \ widetilde {A} \ cup U = U $$
Własność przechodnia
Mając trzy rozmyte zbiory $ \ widetilde {A} $, $ \ widetilde {B} $ i $ \ widetilde {C} $, ta właściwość określa -
$$ Jeśli \: \ widetilde {A} \ subseteq \ widetilde {B} \ subseteq \ widetilde {C}, \: then \: \ widetilde {A} \ subseteq \ widetilde {C} $$
Własność inwolucji
Dla każdego rozmytego zestawu $ \ widetilde {A} $ ta właściwość określa -
$$ \ overline {\ overline {\ widetilde {A}}} = \ widetilde {A} $$
Prawo De Morgana
Prawo to odgrywa kluczową rolę w dowodzeniu tautologii i sprzeczności. To prawo stanowi:
$$ \ overline {{\ widetilde {A} \ cap \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cup \ overline {\ widetilde {B}} $$
$$ \ overline {{\ widetilde {A} \ cup \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cap \ overline {\ widetilde {B}} $$