Teoria de Ressonância Adaptativa
Esta rede foi desenvolvida por Stephen Grossberg e Gail Carpenter em 1987. É baseada na competição e usa um modelo de aprendizagem não supervisionado. As redes da Teoria da Ressonância Adaptativa (ART), como o nome sugere, estão sempre abertas a novas aprendizagens (adaptativas) sem perder os padrões antigos (ressonância). Basicamente, a rede ART é um classificador de vetor que aceita um vetor de entrada e o classifica em uma das categorias, dependendo de qual padrão armazenado se assemelha mais.
Diretor Operacional
A operação principal da classificação ART pode ser dividida nas seguintes fases -
Recognition phase- O vetor de entrada é comparado com a classificação apresentada em cada nó na camada de saída. A saída do neurônio torna-se “1” se melhor corresponder à classificação aplicada, caso contrário, torna-se “0”.
Comparison phase- Nesta fase, uma comparação do vetor de entrada com o vetor da camada de comparação é feita. A condição para o reset é que o grau de similaridade seja menor que o parâmetro de vigilância.
Search phase- Nesta fase, a rede buscará o reset bem como a correspondência realizada nas fases anteriores. Portanto, se não houver um reset e a partida for muito boa, a classificação acabou. Caso contrário, o processo seria repetido e o outro padrão armazenado deve ser enviado para encontrar a correspondência correta.
ART1
É um tipo de ART, que é projetado para agrupar vetores binários. Podemos entender sobre isso com a arquitetura dele.
Arquitetura de ART1
Consiste nas duas unidades a seguir -
Computational Unit - É composto pelo seguinte -
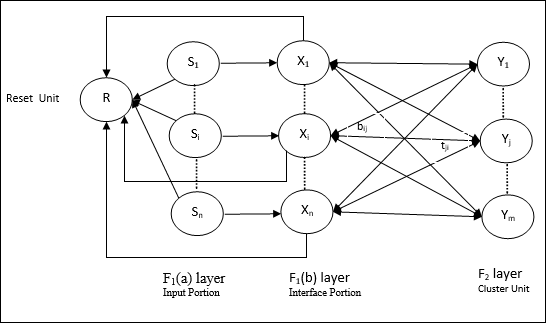
Input unit (F1 layer) - Além disso, possui as seguintes duas partes -
F1(a) layer (Input portion)- Em ART1, não haveria processamento nesta parte em vez de ter apenas os vetores de entrada. Ele é conectado à camada F 1 (b) (parte da interface).
F1(b) layer (Interface portion)- Esta parte combina o sinal da parte de entrada com o da camada F 2 . A camada F 1 (b) está conectada à camada F 2 por meio de pesos ascendentesbije a camada F 2 está conectada à camada F 1 (b) por meio de pesos de cima para baixotji.
Cluster Unit (F2 layer)- Esta é uma camada competitiva. A unidade com a maior entrada líquida é selecionada para aprender o padrão de entrada. A ativação de todas as outras unidades do cluster são definidas como 0.
Reset Mechanism- O trabalho desse mecanismo é baseado na similaridade entre o peso top-down e o vetor de entrada. Agora, se o grau dessa semelhança for menor que o parâmetro de vigilância, então o cluster não tem permissão para aprender o padrão e um descanso aconteceria.
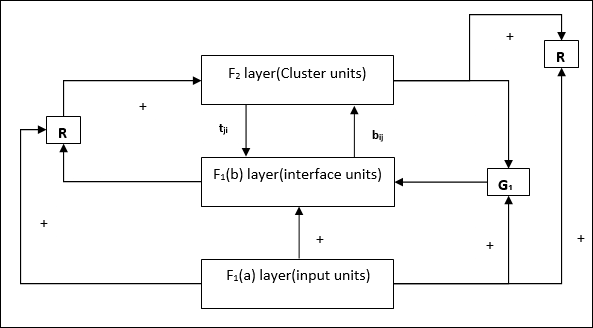
Supplement Unit - Na verdade, o problema com o mecanismo de redefinição é que a camada F2deve ser inibido sob certas condições e também deve estar disponível quando algum aprendizado acontecer. É por isso que duas unidades suplementares, a saber,G1 e G2 é adicionado junto com a unidade de redefinição, R. Eles são chamadosgain control units. Essas unidades recebem e enviam sinais para as outras unidades presentes na rede.‘+’ indica um sinal excitatório, enquanto ‘−’ indica um sinal inibitório.
Parâmetros Usados
Os seguintes parâmetros são usados -
n - Número de componentes no vetor de entrada
m - Número máximo de clusters que podem ser formados
bij- Peso da camada F 1 (b) a F 2 , ou seja, pesos ascendentes
tji- Peso da camada F 2 a F 1 (b), ou seja, pesos de cima para baixo
ρ - Parâmetro de vigilância
||x|| - Norma do vetor x
Algoritmo
Step 1 - Inicialize a taxa de aprendizagem, o parâmetro de vigilância e os pesos da seguinte forma -
$$ \ alpha \:> \: 1 \: \: e \: \: 0 \: <\ rho \: \ leq \: 1 $$
$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: e \: \: t_ {ij} (0) \: = \: 1 $$
Step 2 - Continue a etapa 3-9, quando a condição de parada não for verdadeira.
Step 3 - Continue a etapa 4-6 para cada entrada de treinamento.
Step 4- Defina as ativações de todas as unidades F 1 (a) e F 1 da seguinte forma
F2 = 0 and F1(a) = input vectors
Step 5- O sinal de entrada da camada F 1 (a) para F 1 (b) deve ser enviado como
$$ s_ {i} \: = \: x_ {i} $$
Step 6- Para cada nó F 2 inibido
$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ a condição é yj ≠ -1
Step 7 - Execute os passos 8-10, quando a reinicialização for verdadeira.
Step 8 - Encontre J para yJ ≥ yj para todos os nós j
Step 9- Calcule novamente a ativação em F 1 (b) da seguinte forma
$$ x_ {i} \: = \: sitJi $$
Step 10 - Agora, depois de calcular a norma do vetor x e vetor s, precisamos verificar a condição de redefinição da seguinte forma -
E se ||x||/ ||s|| <parâmetro de vigilância ρ, Entãoinibir nodo J e vá para a etapa 7
Else If ||x||/ ||s|| ≥ parâmetro de vigilância ρe prossiga.
Step 11 - Atualização de peso para o nó J pode ser feito da seguinte forma -
$$ b_ {ij} (novo) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$
$$ t_ {ij} (novo) \: = \: x_ {i} $$
Step 12 - A condição de parada do algoritmo deve ser verificada e pode ser a seguinte -
- Não tem alteração de peso.
- A reinicialização não é executada para unidades.
- Número máximo de épocas atingido.