Rede de memória associada
Esses tipos de redes neurais funcionam com base na associação de padrões, o que significa que podem armazenar padrões diferentes e, no momento de fornecer uma saída, podem produzir um dos padrões armazenados, combinando-os com o padrão de entrada fornecido. Esses tipos de memórias também são chamadosContent-Addressable Memory(CAM). A memória associativa faz uma pesquisa paralela com os padrões armazenados como arquivos de dados.
A seguir estão os dois tipos de memórias associativas que podemos observar -
- Memória Auto Associativa
- Memória heteroassociativa
Memória Auto Associativa
Esta é uma rede neural de camada única na qual o vetor de treinamento de entrada e os vetores de destino de saída são os mesmos. Os pesos são determinados para que a rede armazene um conjunto de padrões.
Arquitetura
Conforme mostrado na figura a seguir, a arquitetura da rede de memória Auto Associativa tem ‘n’ número de vetores de treinamento de entrada e semelhantes ‘n’ número de vetores de destino de saída.
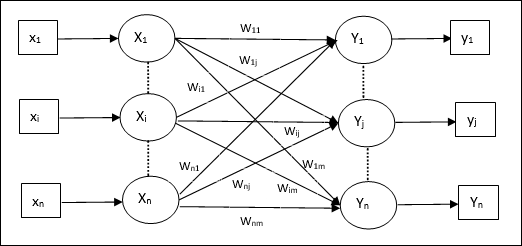
Algoritmo de treinamento
Para treinamento, esta rede está usando a regra de aprendizagem Hebb ou Delta.
Step 1 - Inicialize todos os pesos para zero como wij = 0 (i = 1 to n, j = 1 to n)
Step 2 - Execute as etapas 3-4 para cada vetor de entrada.
Step 3 - Ative cada unidade de entrada da seguinte forma -
$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$
Step 4 - Ative cada unidade de saída da seguinte forma -
$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: para \: n) $$
Step 5 - Ajuste os pesos da seguinte forma -
$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: x_ {i} y_ {j} $$
Algoritmo de teste
Step 1 - Defina os pesos obtidos durante o treinamento para a regra de Hebb.
Step 2 - Execute as etapas 3 a 5 para cada vetor de entrada.
Step 3 - Defina a ativação das unidades de entrada igual à do vetor de entrada.
Step 4 - Calcular a entrada líquida para cada unidade de produção j = 1 to n
$$ y_ {inj} \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 - Aplique a seguinte função de ativação para calcular a saída
$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ - 1 & if \: y_ {inj} \: \ leqslant \: 0 \ end {casos} $$
Memória heteroassociativa
Semelhante à rede de memória autoassociativa, esta também é uma rede neural de camada única. No entanto, nesta rede, o vetor de treinamento de entrada e os vetores de destino de saída não são os mesmos. Os pesos são determinados para que a rede armazene um conjunto de padrões. A rede heteroassociativa é de natureza estática, portanto, não haveria operações não lineares e de atraso.
Arquitetura
Conforme mostrado na figura a seguir, a arquitetura da rede de Memória Hetero Associativa tem ‘n’ número de vetores de treinamento de entrada e ‘m’ número de vetores de destino de saída.
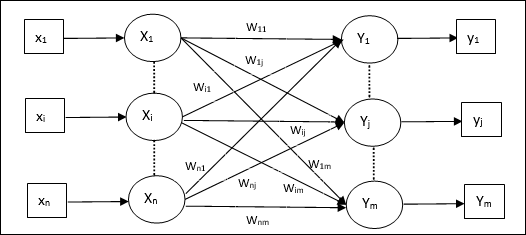
Algoritmo de treinamento
Para treinamento, esta rede está usando a regra de aprendizagem Hebb ou Delta.
Step 1 - Inicialize todos os pesos para zero como wij = 0 (i = 1 to n, j = 1 to m)
Step 2 - Execute as etapas 3-4 para cada vetor de entrada.
Step 3 - Ative cada unidade de entrada da seguinte forma -
$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$
Step 4 - Ative cada unidade de saída da seguinte forma -
$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: a \: m) $$
Step 5 - Ajuste os pesos da seguinte forma -
$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: x_ {i} y_ {j} $$
Algoritmo de teste
Step 1 - Defina os pesos obtidos durante o treinamento para a regra de Hebb.
Step 2 - Execute as etapas 3 a 5 para cada vetor de entrada.
Step 3 - Defina a ativação das unidades de entrada igual à do vetor de entrada.
Step 4 - Calcular a entrada líquida para cada unidade de produção j = 1 to m;
$$ y_ {inj} \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$
Step 5 - Aplique a seguinte função de ativação para calcular a saída
$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ 0 & if \ : y_ {inj} \: = \: 0 \\ - 1 & if \: y_ {inj} \: <\: 0 \ end {cases} $$