Máquina Boltzmann
Estes são processos de aprendizagem estocásticos com estrutura recorrente e são a base das primeiras técnicas de otimização utilizadas em RNA. A Máquina Boltzmann foi inventada por Geoffrey Hinton e Terry Sejnowski em 1985. Mais clareza pode ser observada nas palavras de Hinton sobre a Máquina Boltzmann.
“Uma característica surpreendente dessa rede é que ela usa apenas informações disponíveis localmente. A mudança de peso depende apenas do comportamento das duas unidades que ele conecta, embora a mudança otimize uma medida global ”- Ackley, Hinton 1985.
Alguns pontos importantes sobre a Máquina Boltzmann -
Eles usam estrutura recorrente.
Eles consistem em neurônios estocásticos, que têm um dos dois estados possíveis, 1 ou 0.
Alguns dos neurônios neste são adaptativos (estado livre) e alguns são fixados (estado congelado).
Se aplicarmos o recozimento simulado na rede discreta de Hopfield, ela se tornaria a Máquina de Boltzmann.
Objetivo da Máquina Boltzmann
O objetivo principal da Máquina Boltzmann é otimizar a solução de um problema. É trabalho da Boltzmann Machine otimizar os pesos e as quantidades relacionadas a esse problema específico.
Arquitetura
O diagrama a seguir mostra a arquitetura da máquina Boltzmann. Fica claro no diagrama que é uma matriz bidimensional de unidades. Aqui, os pesos nas interconexões entre as unidades são–p Onde p > 0. Os pesos das auto-conexões são dados porb Onde b > 0.
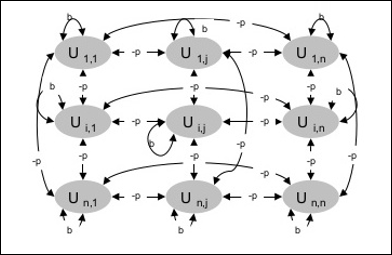
Algoritmo de treinamento
Como sabemos que as máquinas de Boltzmann possuem pesos fixos, não haverá algoritmo de treinamento, pois não precisamos atualizar os pesos na rede. No entanto, para testar a rede, temos que definir os pesos, bem como encontrar a função de consenso (CF).
A máquina Boltzmann possui um conjunto de unidades Ui e Uj e tem conexões bidirecionais neles.
Estamos considerando o peso fixo, digamos wij.
wij ≠ 0 E se Ui e Uj estão conectados.
Também existe uma simetria na interconexão ponderada, ou seja, wij = wji.
wii também existe, ou seja, haveria a auto-conexão entre as unidades.
Para qualquer unidade Ui, seu estado ui seria 1 ou 0.
O objetivo principal da Máquina Boltzmann é maximizar a Função de Consenso (CF) que pode ser dada pela seguinte relação
$$ CF \: = \: \ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$
Agora, quando o estado muda de 1 para 0 ou de 0 para 1, então a mudança no consenso pode ser dada pela seguinte relação -
$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
Aqui ui é o estado atual de Ui.
A variação no coeficiente (1 - 2ui) é dado pela seguinte relação -
$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {cases} +1, & U_ {i} \: is \: atualmente \: off \\ - 1, & U_ {i } \: está \: atualmente \: em \ end {casos} $$
Geralmente, unidade Uinão muda seu estado, mas se o fizer, então as informações estarão residindo no local da unidade. Com essa mudança, também haveria um aumento no consenso da rede.
A probabilidade da rede aceitar a mudança no estado da unidade é dada pela seguinte relação -
$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$
Aqui, Té o parâmetro de controle. Ele diminuirá à medida que CF atinge o valor máximo.
Algoritmo de teste
Step 1 - Inicialize o seguinte para iniciar o treinamento -
- Pesos que representam a restrição do problema
- Parâmetro de controle T
Step 2 - Continue as etapas 3-8, quando a condição de parada não for verdadeira.
Step 3 - Execute as etapas 4-7.
Step 4 - Suponha que um dos estados alterou o peso e escolha o inteiro I, J como valores aleatórios entre 1 e n.
Step 5 - Calcule a mudança de consenso da seguinte forma -
$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$
Step 6 - Calcule a probabilidade de que esta rede aceite a mudança de estado
$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$
Step 7 - Aceite ou rejeite esta mudança da seguinte forma -
Case I - se R < AF, aceite a mudança.
Case II - se R ≥ AF, rejeite a mudança.
Aqui, R é o número aleatório entre 0 e 1.
Step 8 - Reduza o parâmetro de controle (temperatura) da seguinte forma -
T(new) = 0.95T(old)
Step 9 - Teste as condições de parada, que podem ser as seguintes -
- A temperatura atinge um valor especificado
- Não há mudança de estado para um determinado número de iterações