Otimização usando a rede Hopfield
Otimização é uma ação de tornar algo como design, situação, recurso e sistema o mais eficaz possível. Usando uma semelhança entre a função de custo e a função de energia, podemos usar neurônios altamente interconectados para resolver problemas de otimização. Esse tipo de rede neural é a rede de Hopfield, que consiste em uma única camada contendo um ou mais neurônios recorrentes totalmente conectados. Isso pode ser usado para otimização.
Pontos a serem lembrados ao usar a rede Hopfield para otimização -
A função de energia deve ser mínima da rede.
Ele encontrará uma solução satisfatória em vez de selecionar um dos padrões armazenados.
A qualidade da solução encontrada pela rede Hopfield depende significativamente do estado inicial da rede.
Problema do caixeiro viajante
Encontrar o caminho mais curto percorrido pelo vendedor é um dos problemas computacionais, que pode ser otimizado usando a rede neural de Hopfield.
Conceito Básico de TSP
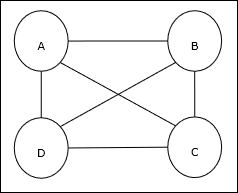
O Problema do Caixeiro Viajante (TSP) é um problema clássico de otimização em que um vendedor tem que viajar ncidades, que estão conectadas entre si, mantendo o custo e a distância percorrida mínimos. Por exemplo, o vendedor tem que percorrer um conjunto de 4 cidades A, B, C, D e o objetivo é encontrar o trajeto circular mais curto, ABC-D, de forma a minimizar o custo, que inclui também o custo da viagem de a última cidade D para a primeira cidade A.
Representação de Matriz
Na verdade, cada passeio do TSP de n-cidades pode ser expresso como n × n matriz de quem ith linha descreve o ithlocalização da cidade. Esta matriz,M, para 4 cidades A, B, C, D pode ser expresso da seguinte forma -
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 e 0 e 1 \ end {bmatrix} $$
Solução da Hopfield Network
Considerando a solução deste TSP pela rede Hopfield, cada nó da rede corresponde a um elemento da matriz.
Cálculo da função de energia
Para ser a solução otimizada, a função de energia deve ser mínima. Com base nas seguintes restrições, podemos calcular a função de energia da seguinte forma -
Restrição-I
A primeira restrição, com base na qual calcularemos a função de energia, é que um elemento deve ser igual a 1 em cada linha da matriz M e outros elementos em cada linha devem ser iguais a 0porque cada cidade pode ocorrer em apenas uma posição no tour do TSP. Esta restrição pode ser matematicamente escrita da seguinte forma -
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: para \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Agora, a função de energia a ser minimizada, com base na restrição acima, conterá um termo proporcional a -
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Restrição-II
Como sabemos, no TSP uma cidade pode ocorrer em qualquer posição no passeio, portanto, em cada coluna da matriz M, um elemento deve ser igual a 1 e os outros elementos devem ser iguais a 0. Esta restrição pode ser matematicamente escrita da seguinte maneira -
$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: para \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Agora, a função de energia a ser minimizada, com base na restrição acima, conterá um termo proporcional a -
$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Cálculo da Função de Custo
Vamos supor uma matriz quadrada de (n × n) denotado por C denota a matriz de custo do TSP para n cidades onde n > 0. A seguir estão alguns parâmetros ao calcular a função de custo -
Cx, y - O elemento da matriz de custo denota o custo de viajar da cidade x para y.
A adjacência dos elementos de A e B pode ser mostrada pela seguinte relação -
$$ M_ {x, i} \: = \: 1 \: \: e \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Como sabemos, em Matrix, o valor de saída de cada nó pode ser 0 ou 1, portanto, para cada par de cidades A, B, podemos adicionar os seguintes termos à função de energia -
$$ \ displaystyle \ sum \ limits_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Com base na função de custo acima e no valor de restrição, a função de energia final E pode ser dado da seguinte forma -
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
Aqui, γ1 e γ2 são duas constantes de pesagem.