Rede Neural Artificial - Guia Rápido

As redes neurais são dispositivos de computação paralela, que é basicamente uma tentativa de fazer um modelo de computador do cérebro. O objetivo principal é desenvolver um sistema que execute várias tarefas computacionais mais rapidamente que os sistemas tradicionais. Essas tarefas incluem reconhecimento e classificação de padrões, aproximação, otimização e armazenamento em cluster de dados.

O que é Rede Neural Artificial?

A Rede Neural Artificial (RNA) é um sistema de computação eficiente cujo tema central é emprestado da analogia das redes neurais biológicas. As RNAs também são chamadas de "sistemas neurais artificiais" ou "sistemas de processamento paralelo distribuído" ou "sistemas conexionistas". A RNA adquire uma grande coleção de unidades que são interconectadas em algum padrão para permitir a comunicação entre as unidades. Essas unidades, também conhecidas como nós ou neurônios, são processadores simples que operam em paralelo.

Cada neurônio está conectado a outro neurônio por meio de um link de conexão. Cada link de conexão está associado a um peso que contém informações sobre o sinal de entrada. Esta é a informação mais útil para os neurônios resolverem um problema específico, porque o peso geralmente excita ou inibe o sinal que está sendo comunicado. Cada neurônio tem um estado interno, que é chamado de sinal de ativação. Os sinais de saída, que são produzidos após combinar os sinais de entrada e a regra de ativação, podem ser enviados para outras unidades.

Uma breve história da ANN

A história da RNA pode ser dividida nas seguintes três eras -

ANN durante os anos 1940 a 1960

Alguns desenvolvimentos importantes desta era são os seguintes -

1943 - Supõe-se que o conceito de rede neural começou com o trabalho do fisiologista Warren McCulloch e do matemático Walter Pitts, quando em 1943 eles modelaram uma rede neural simples usando circuitos elétricos para descrever como os neurônios do cérebro poderiam funcionar .
1949- O livro de Donald Hebb, The Organization of Behavior , expõe o fato de que a ativação repetida de um neurônio por outro aumenta sua força cada vez que eles são usados.
1956 - Uma rede de memória associativa foi introduzida por Taylor.
1958 - Um método de aprendizagem para o modelo de neurônio McCulloch e Pitts chamado Perceptron foi inventado por Rosenblatt.
1960 - Bernard Widrow e Marcian Hoff desenvolveram modelos chamados "ADALINE" e “MADALINE”.

ANN durante os anos 1960 a 1980

Alguns desenvolvimentos importantes desta era são os seguintes -

1961 - Rosenblatt fez uma tentativa sem sucesso, mas propôs o esquema de “retropropagação” para redes multicamadas.
1964 - Taylor construiu um circuito vencedor leva tudo com inibições entre as unidades de saída.
1969 - O perceptron multicamadas (MLP) foi inventado por Minsky e Papert.
1971 - Kohonen desenvolveu memórias associativas.
1976 - Stephen Grossberg e Gail Carpenter desenvolveram a teoria da ressonância adaptativa.

ANN de 1980 até o presente

Alguns desenvolvimentos importantes desta era são os seguintes -

1982 - O principal desenvolvimento foi a abordagem de energia de Hopfield.
1985 - A máquina Boltzmann foi desenvolvida por Ackley, Hinton e Sejnowski.
1986 - Rumelhart, Hinton e Williams introduziram a Regra Delta Generalizada.
1988 - Kosko desenvolveu a Memória Associativa Binária (BAM) e também deu o conceito de Lógica Fuzzy em RNA.

A revisão histórica mostra que um progresso significativo foi feito neste campo. Chips baseados em redes neurais estão surgindo e aplicativos para problemas complexos estão sendo desenvolvidos. Certamente, hoje é um período de transição para a tecnologia de redes neurais.

Neurônio biológico

Uma célula nervosa (neurônio) é uma célula biológica especial que processa informações. De acordo com uma estimativa, existe um grande número de neurônios, aproximadamente 10 ¹¹ com inúmeras interconexões, aproximadamente 10 ¹⁵ .

Diagrama esquemático

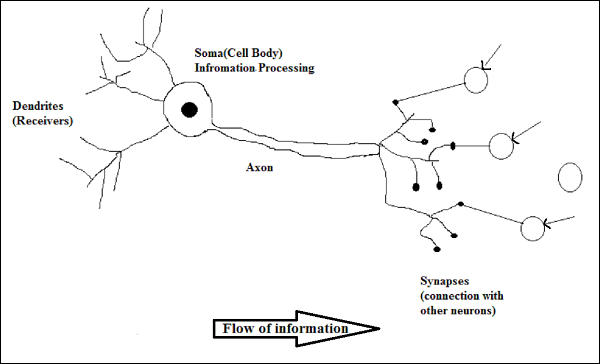
Trabalho de um neurônio biológico

Conforme mostrado no diagrama acima, um neurônio típico consiste nas seguintes quatro partes com a ajuda das quais podemos explicar seu funcionamento -

Dendrites- São ramos em forma de árvore, responsáveis por receber as informações de outros neurônios aos quais está conectado. Em outro sentido, podemos dizer que são como ouvidos de neurônios.
Soma - É o corpo celular do neurônio e é responsável pelo processamento das informações, que eles recebem dos dendritos.
Axon - É como um cabo pelo qual os neurônios enviam as informações.
Synapses - É a conexão entre o axônio e outros dendritos neuronais.

ANN versus BNN

Antes de dar uma olhada nas diferenças entre Rede Neural Artificial (RNA) e Rede Neural Biológica (BNN), vamos dar uma olhada nas semelhanças baseadas na terminologia entre as duas.

Rede Neural Biológica (BNN)	Rede Neural Artificial (ANN)
Soma	Nó
Dendrites	Entrada
Sinapse	Pesos ou interconexões
Axônio	Resultado

A tabela a seguir mostra a comparação entre ANN e BNN com base em alguns critérios mencionados.

Critério	BNN	ANN
Processing	Massivamente paralelo, lento, mas superior a ANN	Massivamente paralelo, rápido, mas inferior do que BNN
Size	10 ¹¹ neurônios e 10 ¹⁵ interconexões	10 ² a 10 ⁴ nós (depende principalmente do tipo de aplicativo e designer de rede)
Learning	Eles podem tolerar ambigüidade	Dados muito precisos, estruturados e formatados são necessários para tolerar a ambigüidade
Fault tolerance	O desempenho é degradado, mesmo com danos parciais	É capaz de desempenho robusto, portanto, tem o potencial de ser tolerante a falhas
Storage capacity	Armazena as informações na sinapse	Armazena as informações em locais de memória contínua

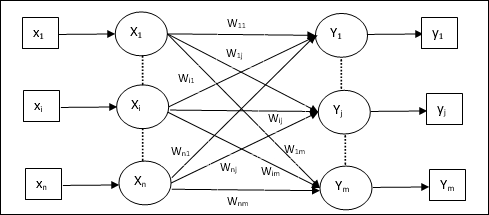
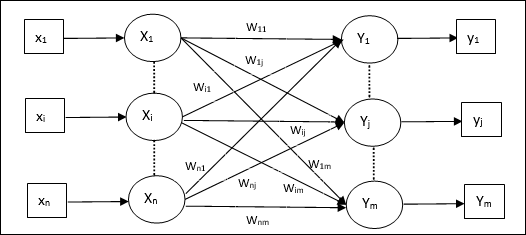
Modelo de Rede Neural Artificial

O diagrama a seguir representa o modelo geral de RNA seguido por seu processamento.

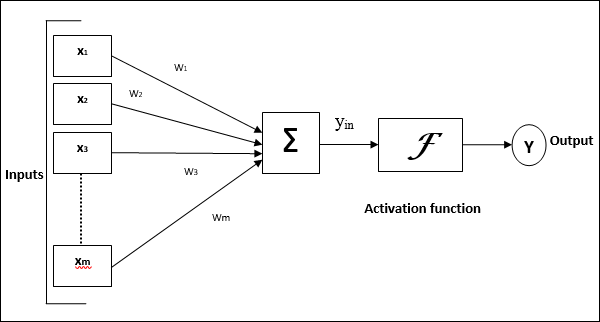
Para o modelo geral de rede neural artificial acima, a entrada líquida pode ser calculada da seguinte forma -

$$ y_ {in} \: = \: x_ {1} .w_ {1} \: + \: x_ {2} .w_ {2} \: + \: x_ {3} .w_ {3} \: \ dotso \: x_ {m} .w_ {m} $$

ou seja, entrada líquida $ y_ {in} \: = \: \ sum_i ^ m \: x_ {i} .w_ {i} $

A saída pode ser calculada aplicando a função de ativação sobre a entrada líquida.

$$ Y \: = \: F (y_ {in}) $$

Saída = função (entrada líquida calculada)

O processamento de ANN depende dos três blocos de construção a seguir -

Topologia de rede
Ajustes de pesos ou aprendizagem
Funções de ativação

Neste capítulo, discutiremos em detalhes sobre esses três blocos de construção da RNA

Topologia de rede

Uma topologia de rede é o arranjo de uma rede junto com seus nós e linhas de conexão. De acordo com a topologia, a RNA pode ser classificada como os seguintes tipos -

Rede Feedforward

É uma rede não recorrente com unidades de processamento / nós em camadas e todos os nós em uma camada estão conectados com os nós das camadas anteriores. A conexão tem pesos diferentes sobre eles. Não há loop de feedback, o que significa que o sinal só pode fluir em uma direção, da entrada para a saída. Pode ser dividido nos seguintes dois tipos -

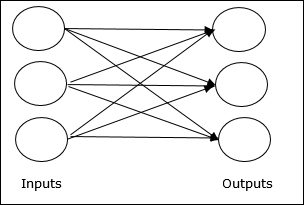
Single layer feedforward network- O conceito é de RNA feedforward tendo apenas uma camada ponderada. Em outras palavras, podemos dizer que a camada de entrada está totalmente conectada à camada de saída.

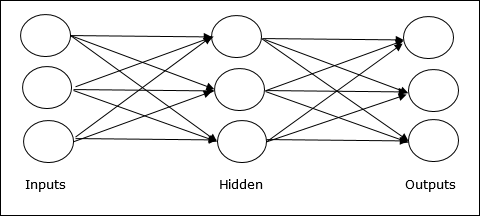
Multilayer feedforward network- O conceito é de RNA feedforward com mais de uma camada ponderada. Como essa rede possui uma ou mais camadas entre a camada de entrada e a de saída, ela é chamada de camadas ocultas.

Rede de Feedback

Como o nome sugere, uma rede de feedback tem caminhos de feedback, o que significa que o sinal pode fluir em ambas as direções usando loops. Isso o torna um sistema dinâmico não linear, que muda continuamente até atingir um estado de equilíbrio. Pode ser dividido nos seguintes tipos -

Recurrent networks- São redes de feedback com malha fechada. A seguir estão os dois tipos de redes recorrentes.
Fully recurrent network - É a arquitetura de rede neural mais simples porque todos os nós estão conectados a todos os outros nós e cada nó funciona como entrada e saída.

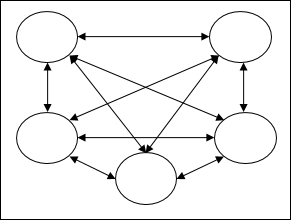
Jordan network - É uma rede em malha fechada na qual a saída irá para a entrada novamente como feedback, conforme mostrado no diagrama a seguir.

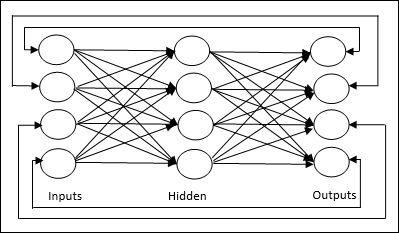
Ajustes de pesos ou aprendizagem

Aprendizagem, em rede neural artificial, é o método de modificar os pesos das conexões entre os neurônios de uma rede especificada. A aprendizagem em RNA pode ser classificada em três categorias, a saber, aprendizagem supervisionada, aprendizagem não supervisionada e aprendizagem por reforço.

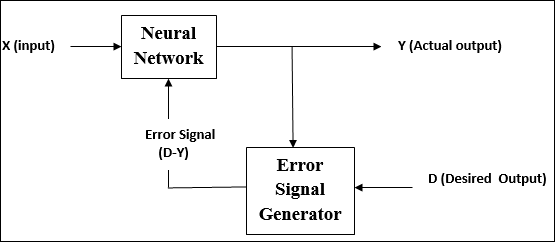
Aprendizagem Supervisionada

Como o nome sugere, esse tipo de aprendizado é feito sob a supervisão de um professor. Este processo de aprendizagem é dependente.

Durante o treinamento da RNA sob aprendizagem supervisionada, o vetor de entrada é apresentado à rede, que dará um vetor de saída. Este vetor de saída é comparado com o vetor de saída desejado. Um sinal de erro é gerado, se houver uma diferença entre a saída real e o vetor de saída desejado. Com base nesse sinal de erro, os pesos são ajustados até que a saída real corresponda à saída desejada.

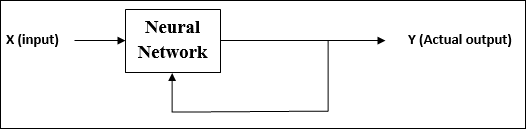
Aprendizagem Não Supervisionada

Como o nome sugere, esse tipo de aprendizagem é feito sem a supervisão de um professor. Este processo de aprendizagem é independente.

Durante o treinamento de RNA sob aprendizagem não supervisionada, os vetores de entrada de tipo semelhante são combinados para formar clusters. Quando um novo padrão de entrada é aplicado, a rede neural fornece uma resposta de saída indicando a classe à qual o padrão de entrada pertence.

Não há feedback do ambiente sobre qual deveria ser a saída desejada e se está correta ou incorreta. Conseqüentemente, neste tipo de aprendizado, a própria rede deve descobrir os padrões e características dos dados de entrada e a relação dos dados de entrada sobre os de saída.

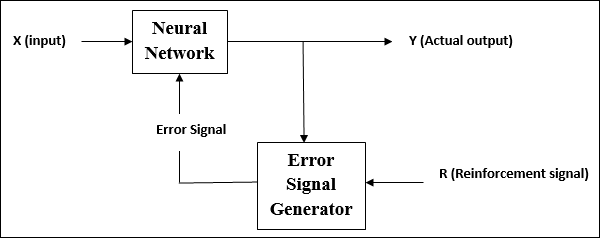
Aprendizagem por Reforço

Como o nome sugere, esse tipo de aprendizado é usado para reforçar ou fortalecer a rede sobre algumas informações críticas. Este processo de aprendizagem é semelhante à aprendizagem supervisionada, mas podemos ter muito menos informações.

Durante o treinamento da rede em aprendizagem por reforço, a rede recebe algum feedback do ambiente. Isso o torna um tanto semelhante ao aprendizado supervisionado. Porém, o feedback obtido aqui é avaliativo e não instrutivo, o que significa que não existe professor como na aprendizagem supervisionada. Após receber o feedback, a rede realiza ajustes dos pesos para obter melhores informações críticas no futuro.

Funções de ativação

Pode ser definido como a força ou esforço extra aplicado sobre a entrada para obter uma saída exata. Em ANN, também podemos aplicar funções de ativação sobre a entrada para obter a saída exata. A seguir estão algumas funções de ativação de interesse -

Função de Ativação Linear

Também é chamada de função de identidade, pois não realiza edição de entrada. Pode ser definido como -

$$ F (x) \: = \: x $$

Função de ativação sigmóide

É de dois tipos, como segue -

Binary sigmoidal function- Esta função de ativação executa a edição de entrada entre 0 e 1. É de natureza positiva. Ele é sempre limitado, o que significa que sua saída não pode ser menor que 0 e maior que 1. Também é estritamente crescente por natureza, o que significa que quanto mais a entrada maior seria a saída. Pode ser definido como

$$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$
Bipolar sigmoidal function- Esta função de ativação executa a edição de entrada entre -1 e 1. Pode ser de natureza positiva ou negativa. É sempre limitado, o que significa que sua saída não pode ser menor que -1 e maior que 1. Também é estritamente crescente na natureza como a função sigmóide. Pode ser definido como

$$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ frac {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$

Como afirmado anteriormente, a RNA é completamente inspirada pela maneira como o sistema nervoso biológico, ou seja, o cérebro humano funciona. A característica mais impressionante do cérebro humano é aprender, portanto, a mesma característica é adquirida pela RNA.

O que está aprendendo na ANN?

Basicamente, aprender significa fazer e adaptar a mudança em si, à medida que ocorre uma mudança no ambiente. A RNA é um sistema complexo ou mais precisamente podemos dizer que é um sistema adaptativo complexo, que pode mudar sua estrutura interna com base na informação que passa por ele.

Por que isso é importante?

Por ser um sistema adaptativo complexo, o aprendizado em RNA implica que uma unidade de processamento é capaz de alterar seu comportamento de entrada / saída devido à mudança no ambiente. A importância do aprendizado em RNA aumenta devido à função de ativação fixa, bem como ao vetor de entrada / saída, quando uma rede particular é construída. Agora, para alterar o comportamento de entrada / saída, precisamos ajustar os pesos.

Classificação

Pode ser definido como o processo de aprender a distinguir os dados de amostras em classes diferentes, encontrando características comuns entre as amostras das mesmas classes. Por exemplo, para realizar o treinamento de RNA, temos alguns exemplos de treinamento com recursos exclusivos, e para realizar seus testes, temos alguns exemplos de teste com outros recursos exclusivos. A classificação é um exemplo de aprendizagem supervisionada.

Regras de aprendizagem de rede neural

Sabemos que, durante o aprendizado da RNA, para alterar o comportamento de entrada / saída, precisamos ajustar os pesos. Portanto, é necessário um método com o qual os pesos possam ser modificados. Esses métodos são chamados de regras de aprendizagem, que são simplesmente algoritmos ou equações. A seguir estão algumas regras de aprendizagem para a rede neural -

Regra de Aprendizagem Hebbian

Essa regra, uma das mais antigas e simples, foi introduzida por Donald Hebb em seu livro A Organização do Comportamento em 1949. É uma espécie de aprendizagem não supervisionada, feed-forward.

Basic Concept - Esta regra é baseada em uma proposta dada por Hebb, que escreveu -

“Quando um axônio da célula A está próximo o suficiente para excitar uma célula B e repetidamente ou persistentemente participa de seu disparo, algum processo de crescimento ou alteração metabólica ocorre em uma ou em ambas as células, de forma que a eficiência de A, como uma das células disparando B , Está melhorado."

A partir do postulado acima, podemos concluir que as conexões entre dois neurônios podem ser fortalecidas se os neurônios dispararem ao mesmo tempo e podem enfraquecer se dispararem em momentos diferentes.

Mathematical Formulation - De acordo com a regra de aprendizagem Hebbian, segue a fórmula para aumentar o peso da conexão a cada passo de tempo.

$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$

Aqui, $ \ Delta w_ {ji} (t) $ ⁡ = incremento pelo qual o peso da conexão aumenta no intervalo de tempo t

$ \ alpha $ = a taxa de aprendizagem positiva e constante

$ x_ {i} (t) $ = o valor de entrada do neurônio pré-sináptico no intervalo de tempo t

$ y_ {i} (t) $ = a saída do neurônio pré-sináptico na mesma etapa de tempo t

Regra de aprendizagem do Perceptron

Esta regra é um erro que corrige o algoritmo de aprendizado supervisionado de redes feedforward de camada única com função de ativação linear, introduzido por Rosenblatt.

Basic Concept- Por ser supervisionado por natureza, para calcular o erro, haveria uma comparação entre a saída desejada / alvo e a saída real. Se houver alguma diferença encontrada, então uma mudança deve ser feita nos pesos da conexão.

Mathematical Formulation - Para explicar sua formulação matemática, suponha que temos 'n' número de vetores de entrada finitos, x (n), junto com seu vetor de saída desejado / alvo t (n), onde n = 1 a N.

Agora, a saída 'y' pode ser calculada, conforme explicado anteriormente com base na entrada líquida, e a função de ativação aplicada sobre essa entrada líquida pode ser expressa da seguinte forma -

$$ y \: = \: f (y_ {in}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {casos} $$

Onde θ é o limiar.

A atualização do peso pode ser feita nos dois casos seguintes -

Case I - quando t ≠ y, então

$$ w (novo) \: = \: w (antigo) \: + \; tx $$

Case II - quando t = y, então

Sem mudança de peso

Regra de aprendizagem Delta (regra de Widrow-Hoff)

É introduzido por Bernard Widrow e Marcian Hoff, também chamado de método Least Mean Square (LMS), para minimizar o erro em todos os padrões de treinamento. É uma espécie de algoritmo de aprendizado supervisionado com função de ativação contínua.

Basic Concept- A base desta regra é a abordagem gradiente-descendente, que continua para sempre. A regra delta atualiza os pesos sinápticos de modo a minimizar a entrada líquida para a unidade de saída e o valor de destino.

Mathematical Formulation - Para atualizar os pesos sinápticos, a regra delta é dada por

$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$

Aqui $ \ Delta w_ {i} $ = mudança de peso para i ^th ⁡padrão;

$ \ alpha $ = a taxa de aprendizagem positiva e constante;

$ x_ {i} $ = o valor de entrada do neurônio pré-sináptico;

$ e_ {j} $ = $ (t \: - \: y_ {in}) $, a diferença entre a saída desejada / alvo e a saída real ⁡ $ y_ {in} $

A regra delta acima é para uma única unidade de saída apenas.

A atualização do peso pode ser feita nos dois casos seguintes -

Case-I - quando t ≠ y, então

$$ w (novo) \: = \: w (antigo) \: + \: \ Delta w $$

Case-II - quando t = y, então

Sem mudança de peso

Regra de aprendizagem competitiva (o vencedor leva tudo)

Ele se preocupa com o treinamento não supervisionado em que os nós de saída tentam competir entre si para representar o padrão de entrada. Para entender esta regra de aprendizagem, devemos entender a rede competitiva que é dada a seguir -

Basic Concept of Competitive Network- Esta rede é como uma rede feedforward de camada única com conexão de feedback entre as saídas. As conexões entre as saídas são do tipo inibidoras, representadas por linhas pontilhadas, o que significa que os concorrentes nunca se sustentam.

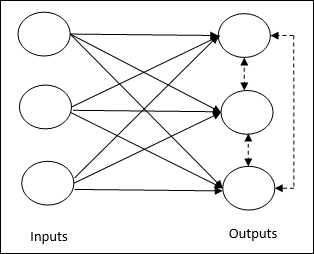
Basic Concept of Competitive Learning Rule- Como dito anteriormente, haverá uma competição entre os nós de saída. Assim, o conceito principal é que durante o treinamento, a unidade de saída com a maior ativação para um determinado padrão de entrada será declarada a vencedora. Essa regra também é chamada de vencedor leva tudo porque apenas o neurônio vencedor é atualizado e o resto dos neurônios são deixados inalterados.

Mathematical formulation - A seguir estão os três fatores importantes para a formulação matemática desta regra de aprendizagem -

Condition to be a winner - Suponha que se um neurônio $ y_ {k} $ ⁡ ⁡ quisesse ser o vencedor, haveria a seguinte condição -

$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & caso contrário \ end {casos} $$

Isso significa que se qualquer neurônio, digamos $ y_ {k} $ ⁡, quiser vencer, então seu campo local induzido (a saída da unidade de soma), digamos $ v_ {k} $, deve ser o maior entre todos os outros neurônios na rede.

Condition of sum total of weight - Outra restrição sobre a regra de aprendizagem competitiva é que a soma total dos pesos para um determinado neurônio de saída será 1. Por exemplo, se considerarmos o neurônio k então -

$$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: \: para \: all \: k $$

Change of weight for winner- Se um neurônio não responde ao padrão de entrada, então nenhum aprendizado ocorre naquele neurônio. No entanto, se um determinado neurônio vencer, os pesos correspondentes serão ajustados da seguinte forma

$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & se \: neurônio \: k \: perdas \ end {casos} $$

Aqui $ \ alpha $ é a taxa de aprendizagem.

Isso mostra claramente que estamos favorecendo o neurônio vencedor ajustando seu peso e, se houver uma perda de neurônio, não precisamos nos preocupar em reajustar seu peso.

Regra de Aprendizagem Outstar

Essa regra, introduzida por Grossberg, está preocupada com o aprendizado supervisionado porque os resultados desejados são conhecidos. É também chamado de aprendizagem de Grossberg.

Basic Concept- Esta regra é aplicada sobre os neurônios dispostos em uma camada. É especialmente projetado para produzir uma saída desejadad da camada de p neurônios.

Mathematical Formulation - Os ajustes de peso nesta regra são calculados da seguinte forma

$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$

Aqui d é a saída de neurônio desejada e $ \ alpha $ é a taxa de aprendizado.

Como o nome sugere, supervised learningocorre sob a supervisão de um professor. Este processo de aprendizagem é dependente. Durante o treinamento da RNA sob aprendizagem supervisionada, o vetor de entrada é apresentado à rede, que produzirá um vetor de saída. Este vetor de saída é comparado com o vetor de saída desejado / alvo. Um sinal de erro é gerado se houver uma diferença entre a saída real e o vetor de saída desejado / alvo. Com base nesse sinal de erro, os pesos seriam ajustados até que a saída real fosse combinada com a saída desejada.

Perceptron

Desenvolvido por Frank Rosenblatt usando o modelo de McCulloch e Pitts, o perceptron é a unidade operacional básica de redes neurais artificiais. Ele emprega regra de aprendizado supervisionado e é capaz de classificar os dados em duas classes.

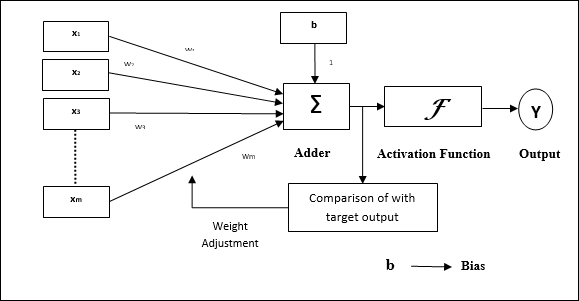
Características operacionais do perceptron: consiste em um único neurônio com um número arbitrário de entradas junto com pesos ajustáveis, mas a saída do neurônio é 1 ou 0 dependendo do limite. Ele também consiste em um viés cujo peso é sempre 1. A figura a seguir fornece uma representação esquemática do perceptron.

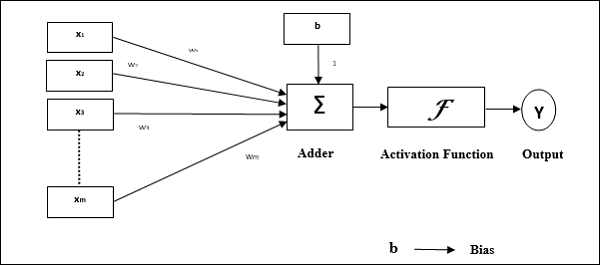
Perceptron, portanto, tem os seguintes três elementos básicos -

Links - Teria um conjunto de links de conexão, que carrega um peso incluindo um viés sempre tendo peso 1.
Adder - Adiciona a entrada depois de multiplicada por seus respectivos pesos.
Activation function- Limita a saída do neurônio. A função de ativação mais básica é uma função de etapa de Heaviside que tem duas saídas possíveis. Esta função retorna 1, se a entrada for positiva, e 0 para qualquer entrada negativa.

Algoritmo de treinamento

A rede Perceptron pode ser treinada para uma única unidade de saída, bem como para várias unidades de saída.

Algoritmo de treinamento para unidade de saída única

Step 1 - Inicialize o seguinte para iniciar o treinamento -

Weights
Bias
Taxa de aprendizagem $ \ alpha $

Para facilitar o cálculo e simplicidade, os pesos e o bias devem ser definidos como 0 e a taxa de aprendizado deve ser definida como 1.

Step 2 - Continue a etapa 3-8 quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada vetor de treinamento x.

Step 4 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 5 - Agora obtenha a entrada líquida com a seguinte relação -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i}. \: w_ {i} $$

Aqui ‘b’ é preconceito e ‘n’ é o número total de neurônios de entrada.

Step 6 - Aplique a seguinte função de ativação para obter a saída final.

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {cases} $$

Step 7 - Ajuste o peso e o viés da seguinte forma -

Case 1 - se y ≠ t então,

$$ w_ {i} (novo) \: = \: w_ {i} (antigo) \: + \: \ alpha \: tx_ {i} $$

$$ b (novo) \: = \: b (antigo) \: + \: \ alpha t $$

Case 2 - se y = t então,

$$ w_ {i} (novo) \: = \: w_ {i} (antigo) $$

$$ b (novo) \: = \: b (antigo) $$

Aqui ‘y’ é a saída real e ‘t’ é a saída desejada / alvo.

Step 8 - Teste a condição de parada, que aconteceria quando não houvesse alteração no peso.

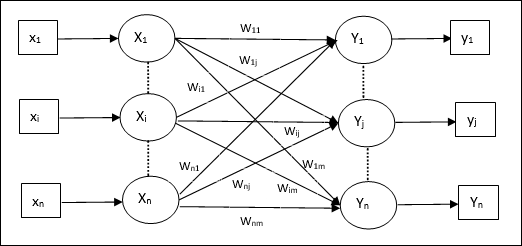
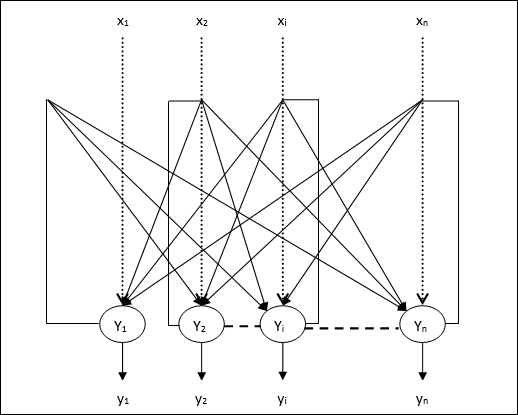
Algoritmo de treinamento para várias unidades de saída

O diagrama a seguir é a arquitetura do perceptron para várias classes de saída.

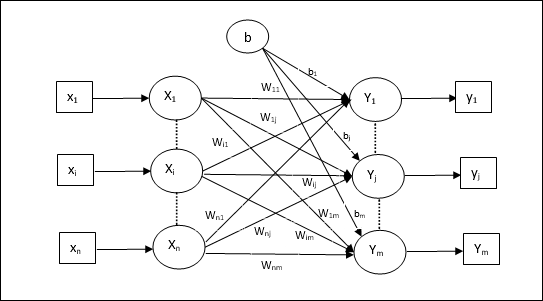
Step 1 - Inicialize o seguinte para iniciar o treinamento -

Weights
Bias
Taxa de aprendizagem $ \ alpha $

Para facilitar o cálculo e simplicidade, os pesos e o bias devem ser definidos como 0 e a taxa de aprendizado deve ser definida como 1.

Step 2 - Continue a etapa 3-8 quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada vetor de treinamento x.

Step 4 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 5 - Obtenha a entrada líquida com a seguinte relação -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {ij} $$

Aqui ‘b’ é preconceito e ‘n’ é o número total de neurônios de entrada.

Step 6 - Aplique a seguinte função de ativação para obter a saída final para cada unidade de saída j = 1 to m -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {inj} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {inj} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {inj} \: <\: - \ theta \ end {cases} $$

Step 7 - Ajuste o peso e o viés para x = 1 to n e j = 1 to m como segue -

Case 1 - se y_j ≠ t_j então,

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: \ alpha \: t_ {j} x_ {i} $$

$$ b_ {j} (novo) \: = \: b_ {j} (antigo) \: + \: \ alpha t_ {j} $$

Case 2 - se y_j = t_j então,

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) $$

$$ b_ {j} (novo) \: = \: b_ {j} (antigo) $$

Aqui ‘y’ é a saída real e ‘t’ é a saída desejada / alvo.

Step 8 - Teste a condição de parada, que acontecerá quando não houver alteração de peso.

Neurônio Linear Adaptativo (Adalino)

Adaline, que significa Adaptive Linear Neuron, é uma rede com uma única unidade linear. Foi desenvolvido por Widrow e Hoff em 1960. Alguns pontos importantes sobre o Adaline são os seguintes -

Ele usa a função de ativação bipolar.
Ele usa a regra delta para treinamento para minimizar o erro quadrático médio (MSE) entre a saída real e a saída desejada / alvo.
Os pesos e a polarização são ajustáveis.

Arquitetura

A estrutura básica do Adaline é semelhante ao perceptron, tendo um loop de feedback extra com a ajuda do qual a saída real é comparada com a saída desejada / alvo. Após comparação com base no algoritmo de treinamento, os pesos e o viés serão atualizados.

Algoritmo de treinamento

Step 1 - Inicialize o seguinte para iniciar o treinamento -

Weights
Bias
Taxa de aprendizagem $ \ alpha $

Para facilitar o cálculo e simplicidade, os pesos e o bias devem ser definidos como 0 e a taxa de aprendizado deve ser definida como 1.

Step 2 - Continue a etapa 3-8 quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada par de treinamento bipolar s:t.

Step 4 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 5 - Obtenha a entrada líquida com a seguinte relação -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {i} $$

Aqui ‘b’ é preconceito e ‘n’ é o número total de neurônios de entrada.

Step 6 - Aplique a seguinte função de ativação para obter a saída final -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {casos} $$

Step 7 - Ajuste o peso e o viés da seguinte forma -

Case 1 - se y ≠ t então,

$$ w_ {i} (novo) \: = \: w_ {i} (antigo) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i} $$

$$ b (novo) \: = \: b (antigo) \: + \: \ alpha (t \: - \: y_ {in}) $$

Case 2 - se y = t então,

$$ w_ {i} (novo) \: = \: w_ {i} (antigo) $$

$$ b (novo) \: = \: b (antigo) $$

Aqui ‘y’ é a saída real e ‘t’ é a saída desejada / alvo.

$ (t \: - \; y_ {in}) $ é o erro calculado.

Step 8 - Teste para condição de parada, que acontecerá quando não houver mudança de peso ou a maior mudança de peso ocorrida durante o treinamento for menor do que a tolerância especificada.

Neurônio Linear Adaptativo Múltiplo (Madaline)

Madaline, que significa Multiple Adaptive Linear Neuron, é uma rede que consiste em muitos Adalines em paralelo. Terá uma única unidade de saída. Alguns pontos importantes sobre Madaline são os seguintes -

É como um perceptron multicamadas, onde Adaline atuará como uma unidade oculta entre a entrada e a camada Madaline.
Os pesos e a polarização entre as camadas de entrada e Adaline, como vemos na arquitetura Adaline, são ajustáveis.
As camadas Adaline e Madaline têm pesos fixos e viés de 1.
O treinamento pode ser feito com a ajuda da regra Delta.

Arquitetura

A arquitetura de Madaline consiste em “n” neurônios da camada de entrada, “m”neurônios da camada Adalina e 1 neurônio da camada Madalina. A camada Adaline pode ser considerada como a camada oculta, pois está entre a camada de entrada e a camada de saída, ou seja, a camada Madaline.

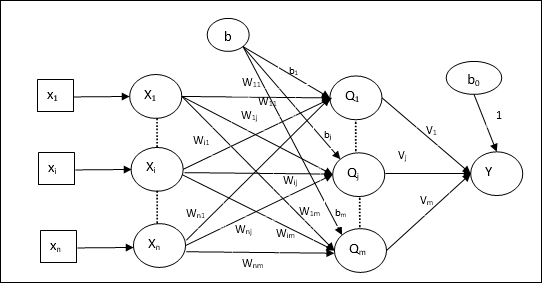
Algoritmo de treinamento

Por enquanto sabemos que apenas os pesos e a polarização entre a entrada e a camada Adaline devem ser ajustados, e os pesos e a polarização entre a Adaline e a camada Madaline são fixos.

Step 1 - Inicialize o seguinte para iniciar o treinamento -

Weights
Bias
Taxa de aprendizagem $ \ alpha $

Para facilitar o cálculo e simplicidade, os pesos e o bias devem ser definidos como 0 e a taxa de aprendizado deve ser definida como 1.

Step 2 - Continue a etapa 3-8 quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada par de treinamento bipolar s:t.

Step 4 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 5 - Obtenha a entrada líquida em cada camada oculta, ou seja, a camada Adaline com a seguinte relação -

$$ Q_ {inj} \: = \: b_ {j} \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: a \: m $$

Aqui ‘b’ é preconceito e ‘n’ é o número total de neurônios de entrada.

Step 6 - Aplicar a seguinte função de ativação para obter a saída final na camada Adaline e Madaline -

$$ f (x) \: = \: \ begin {cases} 1 & if \: x \: \ geqslant \: 0 \\ - 1 & if \: x \: <\: 0 \ end {cases} $ $

Saída na unidade oculta (Adaline)

$$ Q_ {j} \: = \: f (Q_ {inj}) $$

Resultado final da rede

$$ y \: = \: f (y_ {in}) $$

i.e. $ \: \: y_ {inj} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j} $

Step 7 - Calcule o erro e ajuste os pesos da seguinte forma -

Case 1 - se y ≠ t e t = 1 então,

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: \ alpha (1 \: - \: Q_ {inj}) x_ {i} $$

$$ b_ {j} (novo) \: = \: b_ {j} (antigo) \: + \: \ alpha (1 \: - \: Q_ {inj}) $$

Neste caso, os pesos seriam atualizados em Q_j onde a entrada líquida é próxima de 0 porque t = 1.

Case 2 - se y ≠ t e t = -1 então,

$$ w_ {ik} (novo) \: = \: w_ {ik} (antigo) \: + \: \ alpha (-1 \: - \: Q_ {tinta}) x_ {i} $$

$$ b_ {k} (novo) \: = \: b_ {k} (antigo) \: + \: \ alpha (-1 \: - \: Q_ {tinta}) $$

Neste caso, os pesos seriam atualizados em Q_k onde a entrada líquida é positiva porque t = -1.

Aqui ‘y’ é a saída real e ‘t’ é a saída desejada / alvo.

Case 3 - se y = t então

Não haveria mudança nos pesos.

Redes Neurais de Retropropagação

Back Propagation Neural (BPN) é uma rede neural multicamadas que consiste na camada de entrada, pelo menos uma camada oculta e a camada de saída. Como o próprio nome sugere, a retropropagação ocorrerá nesta rede. O erro que é calculado na camada de saída, comparando a saída de destino e a saída real, será propagado de volta para a camada de entrada.

Arquitetura

Conforme mostrado no diagrama, a arquitetura do BPN possui três camadas interconectadas com pesos sobre elas. A camada oculta, assim como a camada de saída, também possui viés, cujo peso é sempre 1, sobre elas. Como fica claro no diagrama, o funcionamento do BPN está em duas fases. Uma fase envia o sinal da camada de entrada para a camada de saída e a outra fase propaga de volta o erro da camada de saída para a camada de entrada.

Algoritmo de treinamento

Para o treinamento, o BPN usará a função de ativação sigmóide binária. A formação do BPN terá as três fases seguintes.

Phase 1 - Fase de Feed Forward
Phase 2 - Retropropagação de erro
Phase 3 - Atualização de pesos

Todas essas etapas serão concluídas no algoritmo da seguinte forma

Step 1 - Inicialize o seguinte para iniciar o treinamento -

Weights
Taxa de aprendizagem $ \ alpha $

Para fácil cálculo e simplicidade, use alguns pequenos valores aleatórios.

Step 2 - Continue a etapa 3-11 quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-10 para cada par de treinamento.

Fase 1

Step 4 - Cada unidade de entrada recebe um sinal de entrada x_i e envia para a unidade oculta para todos i = 1 to n

Step 5 - Calcule a entrada líquida na unidade oculta usando a seguinte relação -

$$ Q_ {inj} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: j \: = \ : 1 \: a \: p $$

Aqui b_0j é o preconceito na unidade oculta, v_ij é o peso sobre j unidade da camada oculta proveniente de i unidade da camada de entrada.

Agora calcule a saída líquida aplicando a seguinte função de ativação

$$ Q_ {j} \: = \: f (Q_ {inj}) $$

Envie esses sinais de saída das unidades da camada oculta para as unidades da camada de saída.

Step 6 - Calcule a entrada líquida na unidade da camada de saída usando a seguinte relação -

$$ y_ {tinta} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: a \: m $$

Aqui b_0k Este é o viés na unidade de saída, w_jk é o peso sobre k unidade da camada de saída proveniente de j unidade da camada oculta.

Calcule a saída líquida aplicando a seguinte função de ativação

$$ y_ {k} \: = \: f (y_ {tinta}) $$

Fase 2

Step 7 - Calcule o termo de correção de erro, em correspondência com o padrão de destino recebido em cada unidade de saída, como segue -

$$ \ delta_ {k} \: = \ :( t_ {k} \: - \: y_ {k}) f ^ {'} (y_ {tinta}) $$

Com base nisso, atualize o peso e o viés da seguinte forma -

$$ \ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij} $$

$$ \ Delta b_ {0k} \: = \: \ alpha \ delta_ {k} $$

Então, envie $ \ delta_ {k} $ de volta para a camada oculta.

Step 8 - Agora, cada unidade oculta será a soma de suas entradas delta das unidades de saída.

$$ \ delta_ {inj} \: = \: \ displaystyle \ sum \ limits_ {k = 1} ^ m \ delta_ {k} \: w_ {jk} $$

O termo de erro pode ser calculado da seguinte forma -

$$ \ delta_ {j} \: = \: \ delta_ {inj} f ^ {'} (Q_ {inj}) $$

Com base nisso, atualize o peso e o viés da seguinte forma -

$$ \ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i} $$

$$ \ Delta b_ {0j} \: = \: \ alpha \ delta_ {j} $$

Fase 3

Step 9 - Cada unidade de saída (y_kk = 1 to m) atualiza o peso e o viés da seguinte forma -

$$ v_ {jk} (novo) \: = \: v_ {jk} (antigo) \: + \: \ Delta v_ {jk} $$

$$ b_ {0k} (novo) \: = \: b_ {0k} (antigo) \: + \: \ Delta b_ {0k} $$

Step 10 - Cada unidade de saída (z_jj = 1 to p) atualiza o peso e o viés da seguinte forma -

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: \ Delta w_ {ij} $$

$$ b_ {0j} (novo) \: = \: b_ {0j} (antigo) \: + \: \ Delta b_ {0j} $$

Step 11 - Verifique a condição de parada, que pode ser o número de épocas alcançadas ou a saída de destino corresponde à saída real.

Regra de aprendizagem Delta generalizada

A regra delta funciona apenas para a camada de saída. Por outro lado, regra delta generalizada, também chamada deback-propagation regra, é uma forma de criar os valores desejados da camada oculta.

Formulação Matemática

Para a função de ativação $ y_ {k} \: = \: f (y_ {tinta}) $ a derivação da entrada líquida na camada Oculta, bem como na camada de saída pode ser dada por

$$ y_ {ink} \: = \: \ displaystyle \ sum \ limits_i \: z_ {i} w_ {jk} $$

E $ \: \: y_ {inj} \: = \: \ sum_i x_ {i} v_ {ij} $

Agora, o erro que deve ser minimizado é

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2 $$

Ao usar a regra da cadeia, temos

$$ \ frac {\ partial E} {\ partial w_ {jk}} \: = \: \ frac {\ partial} {\ partial w_ {jk}} (\ frac {1} {2} \ displaystyle \ sum \ limites_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2) $$

$$ = \: \ frac {\ partial} {\ partial w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {ink})] ^ 2 \ rgroup $$

$$ = \: - [t_ {k} \: - \: y_ {k}] \ frac {\ partial} {\ partial w_ {jk}} f (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f (y_ {tinta}) \ frac {\ parcial} {\ parcial w_ {jk}} (y_ {tinta}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {tinta}) z_ {j} $$

Agora vamos dizer $ \ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {tinta}) $

Os pesos nas conexões com a unidade oculta z_j pode ser dado por -

$$ \ frac {\ partial E} {\ partial v_ {ij}} \: = \: - \ displaystyle \ sum \ limits_ {k} \ delta_ {k} \ frac {\ partial} {\ partial v_ {ij} } \ :( y_ {ink}) $$

Colocando o valor de $ y_ {ink} $ obteremos o seguinte

$$ \ delta_ {j} \: = \: - \ displaystyle \ sum \ limits_ {k} \ delta_ {k} w_ {jk} f ^ {'} (z_ {inj}) $$

A atualização do peso pode ser feita da seguinte forma -

Para a unidade de saída -

$$ \ Delta w_ {jk} \: = \: - \ alpha \ frac {\ partial E} {\ partial w_ {jk}} $$

$$ = \: \ alpha \: \ delta_ {k} \: z_ {j} $$

Para a unidade oculta -

$$ \ Delta v_ {ij} \: = \: - \ alpha \ frac {\ partial E} {\ partial v_ {ij}} $$

$$ = \: \ alpha \: \ delta_ {j} \: x_ {i} $$

Como o nome sugere, esse tipo de aprendizagem é feito sem a supervisão de um professor. Este processo de aprendizagem é independente. Durante o treinamento de RNA sob aprendizagem não supervisionada, os vetores de entrada de tipo semelhante são combinados para formar clusters. Quando um novo padrão de entrada é aplicado, a rede neural fornece uma resposta de saída indicando a classe à qual o padrão de entrada pertence. Nesse caso, não haveria feedback do ambiente sobre qual deveria ser a saída desejada e se está correta ou incorreta. Portanto, neste tipo de aprendizagem, a própria rede deve descobrir os padrões, características dos dados de entrada e a relação dos dados de entrada sobre a saída.

Vencedor-leva-todas as redes

Esses tipos de redes são baseados na regra de aprendizado competitivo e usarão a estratégia em que ele escolhe o neurônio com o maior total de entradas como vencedor. As conexões entre os neurônios de saída mostram a competição entre eles e um deles seria 'ON', o que significa que seria o vencedor e os outros seriam 'OFF'.

A seguir estão algumas das redes baseadas neste conceito simples, usando aprendizagem não supervisionada.

Hamming Network

Na maioria das redes neurais que usam aprendizagem não supervisionada, é essencial calcular a distância e realizar comparações. Este tipo de rede é a rede de Hamming, onde para cada vetor de entrada dado, seria agrupado em grupos diferentes. A seguir estão alguns recursos importantes da Hamming Networks -

Lippmann começou a trabalhar em redes Hamming em 1987.
É uma rede de camada única.
As entradas podem ser binárias {0, 1} ou bipolares {-1, 1}.
Os pesos da rede são calculados pelos vetores exemplares.
É uma rede de pesos fixos, o que significa que os pesos permaneceriam os mesmos mesmo durante o treinamento.

Rede máxima

Esta também é uma rede de peso fixo, que serve como uma sub-rede para selecionar o nó com a entrada mais alta. Todos os nós estão totalmente interconectados e existem pesos simétricos em todas essas interconexões ponderadas.

Arquitetura

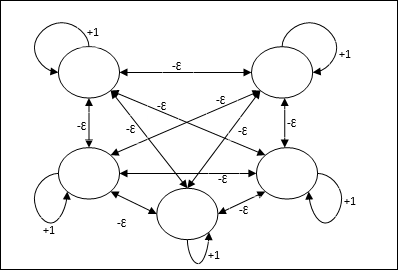
Ele usa o mecanismo que é um processo iterativo e cada nó recebe entradas inibitórias de todos os outros nós por meio de conexões. O único nó cujo valor é máximo seria ativo ou vencedor e as ativações de todos os outros nós seriam inativas. Max Net usa a função de ativação de identidade com $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {cases} $$

A tarefa desta rede é realizada pelo peso de autoexcitação de +1 e magnitude de inibição mútua, que é definida como [0 <ɛ <$ \ frac {1} {m} $] onde “m” é o número total de nós.

Aprendizagem Competitiva em ANN

Ele está relacionado ao treinamento não supervisionado no qual os nós de saída tentam competir entre si para representar o padrão de entrada. Para entender essa regra de aprendizado, teremos que entender a rede competitiva, que é explicada a seguir -

Conceito Básico de Rede Competitiva

Essa rede é como uma rede feed-forward de camada única, com conexão de feedback entre as saídas. As conexões entre as saídas são do tipo inibidoras, que são representadas por linhas pontilhadas, o que significa que os concorrentes nunca se sustentam.

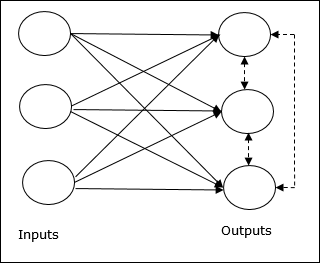
Conceito Básico de Regra de Aprendizagem Competitiva

Como dito anteriormente, haveria competição entre os nós de saída, então o conceito principal é - durante o treinamento, a unidade de saída que tem a maior ativação para um determinado padrão de entrada, será declarada a vencedora. Essa regra também é chamada de vencedor leva tudo porque apenas o neurônio vencedor é atualizado e o resto dos neurônios são deixados inalterados.

Formulação Matemática

A seguir estão os três fatores importantes para a formulação matemática desta regra de aprendizagem -

Condição para ser um vencedor

Suponha que se um neurônio y_k quer ser o vencedor, haveria a seguinte condição

$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 & caso contrário \ end {casos} $$

Isso significa que se algum neurônio, digamos, y_k quer ganhar, então seu campo local induzido (a saída da unidade de soma), digamos v_k, deve ser o maior entre todos os outros neurônios da rede.
Condição da soma total do peso

Outra restrição sobre a regra de aprendizagem competitiva é a soma total de pesos para um determinado neurônio de saída será 1. Por exemplo, se considerarmos o neurônio k então

$$ \ displaystyle \ sum \ limits_ {k} w_ {kj} \: = \: 1 \: \: \: \: \: para \: todos \: \: k $$
Mudança de peso para o vencedor

Se um neurônio não responde ao padrão de entrada, então nenhum aprendizado ocorre naquele neurônio. No entanto, se um determinado neurônio vencer, os pesos correspondentes serão ajustados da seguinte forma -

$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0 e se \: neurônio \: k \: perdas \ end {casos} $$

Aqui $ \ alpha $ é a taxa de aprendizagem.

Isso mostra claramente que estamos favorecendo o neurônio vencedor ajustando seu peso e, se um neurônio for perdido, não precisamos nos preocupar em reajustar seu peso.

Algoritmo de agrupamento K-means

K-means é um dos algoritmos de agrupamento mais populares em que usamos o conceito de procedimento de partição. Começamos com uma partição inicial e movemos padrões repetidamente de um cluster para outro, até obter um resultado satisfatório.

Algoritmo

Step 1 - Selecione kpontos como os centróides iniciais. Inicializark protótipos (w₁,…,w_k), por exemplo, podemos identificá-los com vetores de entrada escolhidos aleatoriamente -

$$ W_ {j} \: = \: i_ {p}, \: \: \: onde \: j \: \ in \ lbrace1, ...., k \ rbrace \: e \: p \: \ em \ lbrace1, ...., n \ rbrace $$

Cada cluster C_j está associado ao protótipo w_j.

Step 2 - Repita a etapa 3-5 até que E não diminua mais ou a associação do cluster não seja mais alterada.

Step 3 - Para cada vetor de entrada i_p Onde p ∈ {1,…,n}, colocar i_p no cluster C_j* com o protótipo mais próximo w_j* tendo a seguinte relação

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Para cada cluster C_j, Onde j ∈ { 1,…,k}, atualize o protótipo w_j para ser o centroide de todas as amostras atualmente em C_j , de modo a

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Calcule o erro de quantização total da seguinte forma -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Neocognitron

É uma rede feedforward multicamadas, desenvolvida por Fukushima na década de 1980. Este modelo é baseado no aprendizado supervisionado e é usado para reconhecimento de padrões visuais, principalmente de caracteres escritos à mão. É basicamente uma extensão da rede Cognitron, que também foi desenvolvida por Fukushima em 1975.

Arquitetura

É uma rede hierárquica, que compreende muitas camadas e há um padrão de conectividade local nessas camadas.

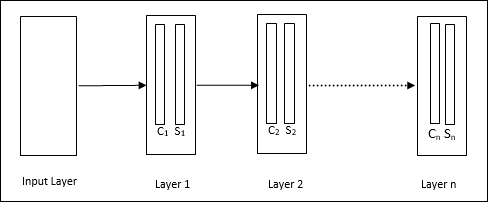
Como vimos no diagrama acima, o neocognitron é dividido em diferentes camadas conectadas e cada camada possui duas células. A explicação dessas células é a seguinte -

S-Cell - É chamada de célula simples, que é treinada para responder a um determinado padrão ou grupo de padrões.

C-Cell- É chamada de célula complexa, que combina a saída da célula S e simultaneamente diminui o número de unidades em cada matriz. Em outro sentido, a célula C desloca o resultado da célula S.

Algoritmo de treinamento

Descobriu-se que o treinamento do neocognitron progride camada por camada. Os pesos da camada de entrada para a primeira camada são treinados e congelados. Em seguida, os pesos da primeira camada para a segunda são treinados e assim por diante. Os cálculos internos entre a célula S e a célula C dependem dos pesos provenientes das camadas anteriores. Portanto, podemos dizer que o algoritmo de treinamento depende dos cálculos nas células S e C.

Cálculos na célula S

A célula S possui o sinal excitatório recebido da camada anterior e possui sinais inibitórios obtidos dentro da mesma camada.

$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$

Aqui, t_i é o peso fixo e c_i é a saída da célula C.

A entrada em escala da célula S pode ser calculada da seguinte forma -

$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$

Aqui, $ e \: = \: \ sum_i c_ {i} w_ {i} $

w_i é o peso ajustado de célula C para célula S.

w₀ é o peso ajustável entre a entrada e a célula S.

v é a entrada excitatória da célula C.

A ativação do sinal de saída é,

$$ s \: = \: \ begin {cases} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {cases} $$

Cálculos na célula C

A entrada líquida da camada C é

$$ C \: = \: \ displaystyle \ sum \ limits_i s_ {i} x_ {i} $$

Aqui, s_i é a saída da célula S e x_i é o peso fixo da célula S para a célula C.

O resultado final é o seguinte -

$$ C_ {out} \: = \: \ begin {cases} \ frac {C} {a + C}, & if \: C> 0 \\ 0, & caso contrário \ end {cases} $$

Aqui ‘a’ é o parâmetro que depende do desempenho da rede.

Learning Vector Quantization (LVQ), diferente da Vector quantization (VQ) e Kohonen Self-Organizing Maps (KSOM), é basicamente uma rede competitiva que utiliza aprendizagem supervisionada. Podemos defini-lo como um processo de classificação dos padrões em que cada unidade de saída representa uma classe. Por usar aprendizado supervisionado, a rede receberá um conjunto de padrões de treinamento com classificação conhecida junto com uma distribuição inicial da classe de saída. Depois de completar o processo de treinamento, LVQ classificará um vetor de entrada atribuindo-o à mesma classe da unidade de saída.

Arquitetura

A figura a seguir mostra a arquitetura do LVQ, que é bastante semelhante à arquitetura do KSOM. Como podemos ver, existem“n” número de unidades de entrada e “m”número de unidades de saída. As camadas estão totalmente interconectadas com pesos sobre elas.

Parâmetros Usados

A seguir estão os parâmetros usados no processo de treinamento LVQ, bem como no fluxograma

x= vetor de treinamento (x ₁ , ..., x _i , ..., x _n )
T = classe para vetor de treinamento x
w_j = vetor de peso para j^th unidade de saída
C_j = classe associada ao j^th unidade de saída

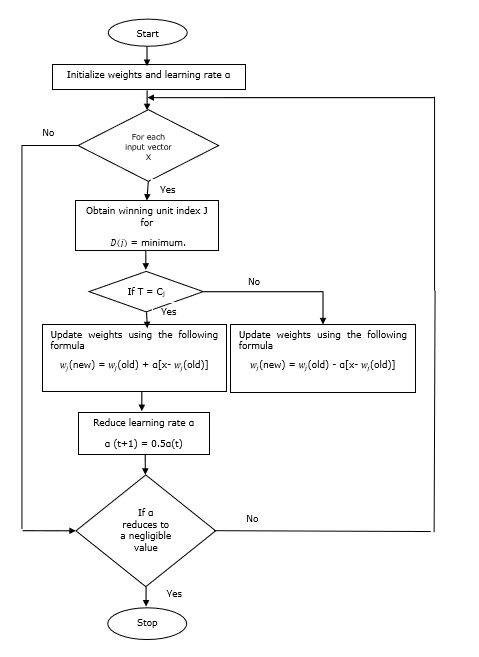
Algoritmo de treinamento

Step 1 - Inicialize os vetores de referência, o que pode ser feito da seguinte maneira -

Step 1(a) - A partir de um determinado conjunto de vetores de treinamento, pegue o primeiro “m”(Número de clusters) vetores de treinamento e usá-los como vetores de peso. Os vetores restantes podem ser usados para treinamento.
Step 1(b) - Atribuir o peso inicial e classificação aleatoriamente.
Step 1(c) - Aplicar o método de agrupamento K-means.

Step 2 - Inicializar vetor de referência $ \ alpha $

Step 3 - Continue com os passos 4-9, se a condição para parar este algoritmo não for atendida.

Step 4 - Siga as etapas 5 a 6 para cada vetor de entrada de treinamento x.

Step 5 - Calcular o quadrado da distância euclidiana para j = 1 to m e i = 1 to n

$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 6 - Obtenha a unidade vencedora J Onde D(j) é mínimo.

Step 7 - Calcule o novo peso da unidade vencedora pela seguinte relação -

E se T = C_j então $ w_ {j} (novo) \: = \: w_ {j} (antigo) \: + \: \ alpha [x \: - \: w_ {j} (antigo)] $

E se T ≠ C_j então $ w_ {j} (novo) \: = \: w_ {j} (antigo) \: - \: \ alpha [x \: - \: w_ {j} (antigo)] $

Step 8 - Reduza a taxa de aprendizagem $ \ alpha $.

Step 9- Teste a condição de parada. Pode ser o seguinte -

Número máximo de épocas atingido.
Taxa de aprendizagem reduzida a um valor insignificante.

Fluxograma

Variantes

Três outras variantes, nomeadamente LVQ2, LVQ2.1 e LVQ3, foram desenvolvidas por Kohonen. A complexidade em todas essas três variantes, devido ao conceito de que tanto a unidade vencedora quanto a segunda colocada aprenderão, é maior do que em LVQ.

LVQ2

Conforme discutido, o conceito de outras variantes de LVQ acima, a condição de LVQ2 é formada por janela. Esta janela será baseada nos seguintes parâmetros -

x - o vetor de entrada atual
y_c - o vetor de referência mais próximo de x
y_r - o outro vetor de referência, que é o próximo mais próximo de x
d_c - a distância de x para y_c
d_r - a distância de x para y_r

O vetor de entrada x cai na janela, se

$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: e \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$

Aqui, $ \ theta $ é o número de amostras de treinamento.

A atualização pode ser feita com a seguinte fórmula -

$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)

$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)

Aqui $ \ alpha $ é a taxa de aprendizagem.

LVQ2.1

Em LVQ2.1, tomaremos os dois vetores mais próximos, a saber y_c1 e y_c2 e a condição da janela é a seguinte -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$

$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$

A atualização pode ser feita com a seguinte fórmula -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Aqui, $ \ alpha $ é a taxa de aprendizado.

LVQ3

Em LVQ3, tomaremos os dois vetores mais próximos, a saber y_c1 e y_c2 e a condição da janela é a seguinte -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$

Aqui $ \ theta \ approx 0.2 $

A atualização pode ser feita com a seguinte fórmula -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Aqui $ \ beta $ é o múltiplo da taxa de aprendizagem $ \ alpha $ e $\beta\:=\:m \alpha(t)$ para cada 0.1 < m < 0.5

Esta rede foi desenvolvida por Stephen Grossberg e Gail Carpenter em 1987. É baseada na competição e usa um modelo de aprendizagem não supervisionado. As redes da Teoria da Ressonância Adaptativa (ART), como o nome sugere, estão sempre abertas a novas aprendizagens (adaptativas) sem perder os padrões antigos (ressonância). Basicamente, a rede ART é um classificador de vetor que aceita um vetor de entrada e o classifica em uma das categorias, dependendo de qual padrão armazenado se assemelha mais.

Diretor Operacional

A operação principal da classificação ART pode ser dividida nas seguintes fases -

Recognition phase- O vetor de entrada é comparado com a classificação apresentada em cada nó na camada de saída. A saída do neurônio torna-se “1” se melhor corresponder à classificação aplicada, caso contrário, torna-se “0”.
Comparison phase- Nesta fase, uma comparação do vetor de entrada com o vetor da camada de comparação é feita. A condição para o reset é que o grau de similaridade seja menor que o parâmetro de vigilância.
Search phase- Nesta fase, a rede buscará o reset bem como a correspondência realizada nas fases anteriores. Portanto, se não houver um reset e a partida for muito boa, a classificação acabou. Caso contrário, o processo seria repetido e o outro padrão armazenado deve ser enviado para encontrar a correspondência correta.

ART1

É um tipo de ART, que é projetado para agrupar vetores binários. Podemos entender sobre isso com a arquitetura dele.

Arquitetura de ART1

Consiste nas duas unidades a seguir -

Computational Unit - É composto pelo seguinte -

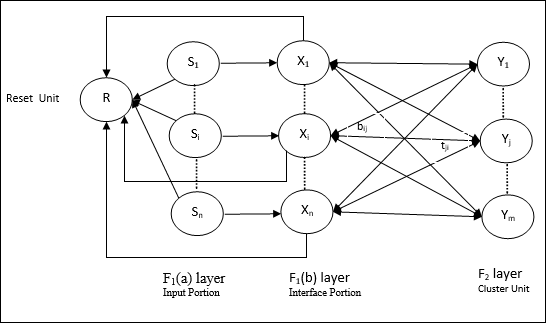
Input unit (F₁ layer) - Além disso, possui as seguintes duas partes -
- F₁(a) layer (Input portion)- Em ART1, não haveria processamento nesta parte em vez de ter apenas os vetores de entrada. Ele é conectado à camada F ₁ (b) (parte da interface).
- F₁(b) layer (Interface portion)- Esta parte combina o sinal da parte de entrada com o da camada F ₂ . A camada F ₁ (b) está conectada à camada F ₂ por meio de pesos ascendentesb_ije a camada F ₂ está conectada à camada F ₁ (b) por meio de pesos de cima para baixot_ji.
Cluster Unit (F₂ layer)- Esta é uma camada competitiva. A unidade com a maior entrada líquida é selecionada para aprender o padrão de entrada. A ativação de todas as outras unidades do cluster são definidas como 0.
Reset Mechanism- O trabalho desse mecanismo é baseado na similaridade entre o peso top-down e o vetor de entrada. Agora, se o grau dessa semelhança for menor que o parâmetro de vigilância, então o cluster não tem permissão para aprender o padrão e um descanso aconteceria.

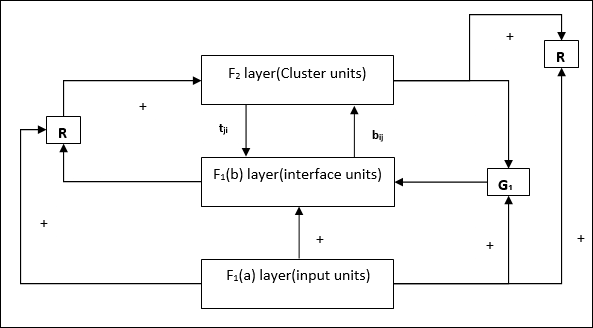
Supplement Unit - Na verdade, o problema com o mecanismo de redefinição é que a camada F₂deve ser inibido sob certas condições e também deve estar disponível quando algum aprendizado acontecer. É por isso que duas unidades suplementares, a saber,G₁ e G₂ é adicionado junto com a unidade de redefinição, R. Eles são chamadosgain control units. Essas unidades recebem e enviam sinais para as outras unidades presentes na rede.‘+’ indica um sinal excitatório, enquanto ‘−’ indica um sinal inibitório.

Parâmetros Usados

Os seguintes parâmetros são usados -

n - Número de componentes no vetor de entrada
m - Número máximo de clusters que podem ser formados
b_ij- Peso da camada F ₁ (b) a F ₂ , ou seja, pesos ascendentes
t_ji- Peso da camada F ₂ a F ₁ (b), ou seja, pesos de cima para baixo
ρ - Parâmetro de vigilância
||x|| - Norma do vetor x

Algoritmo

Step 1 - Inicialize a taxa de aprendizagem, o parâmetro de vigilância e os pesos da seguinte forma -

$$ \ alpha \:> \: 1 \: \: e \: \: 0 \: <\ rho \: \ leq \: 1 $$

$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: e \: \: t_ {ij} (0) \: = \: 1 $$

Step 2 - Continue a etapa 3-9, quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada entrada de treinamento.

Step 4- Defina as ativações de todas as unidades F ₁ (a) e F _{1 da} seguinte forma

F₂ = 0 and F₁(a) = input vectors

Step 5- O sinal de entrada da camada F ₁ (a) para F ₁ (b) deve ser enviado como

$$ s_ {i} \: = \: x_ {i} $$

Step 6- Para cada nó F ₂ inibido

$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ a condição é y_j ≠ -1

Step 7 - Execute os passos 8-10, quando a reinicialização for verdadeira.

Step 8 - Encontre J para y_J ≥ y_j para todos os nós j

Step 9- Calcule novamente a ativação em F ₁ (b) da seguinte forma

$$ x_ {i} \: = \: sitJi $$

Step 10 - Agora, depois de calcular a norma do vetor x e vetor s, precisamos verificar a condição de redefinição da seguinte forma -

E se ||x||/ ||s|| <parâmetro de vigilância ρ, ⁡Entãoinibir ⁡nodo J e vá para a etapa 7

Else If ||x||/ ||s|| ≥ parâmetro de vigilância ρe prossiga.

Step 11 - Atualização de peso para o nó J pode ser feito da seguinte forma -

$$ b_ {ij} (novo) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$

$$ t_ {ij} (novo) \: = \: x_ {i} $$

Step 12 - A condição de parada do algoritmo deve ser verificada e pode ser a seguinte -

Não tem alteração de peso.
A reinicialização não é executada para unidades.
Número máximo de épocas atingido.

Suponha que temos algum padrão de dimensões arbitrárias, no entanto, precisamos deles em uma dimensão ou duas dimensões. Então, o processo de mapeamento de recursos seria muito útil para converter o amplo espaço de padrões em um espaço de recursos típico. Agora, surge a pergunta: por que exigimos um mapa de características auto-organizáveis? A razão é que, junto com a capacidade de converter as dimensões arbitrárias em 1-D ou 2-D, ele também deve ter a capacidade de preservar a topologia vizinha.

Topologias vizinhas em Kohonen SOM

Pode haver várias topologias, no entanto, as duas topologias a seguir são as mais usadas -

Topologia de grade retangular

Essa topologia tem 24 nós na grade distance-2, 16 nós na grade distance-1 e 8 nós na grade distance-0, o que significa que a diferença entre cada grade retangular é de 8 nós. A unidade vencedora é indicada por #.

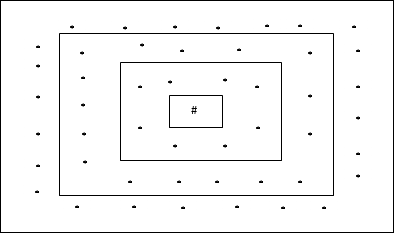
Topologia de grade hexagonal

Essa topologia tem 18 nós na grade distance-2, 12 nós na grade distance-1 e 6 nós na grade distance-0, o que significa que a diferença entre cada grade retangular é de 6 nós. A unidade vencedora é indicada por #.

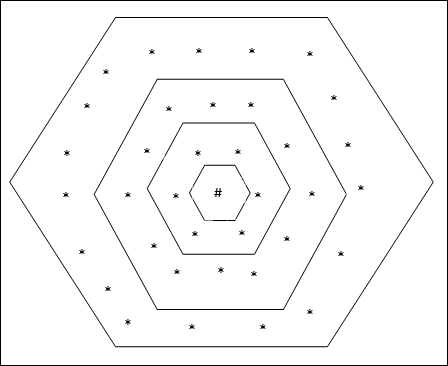
Arquitetura

A arquitetura do KSOM é semelhante à da rede competitiva. Com a ajuda de esquemas de vizinhança, discutidos anteriormente, o treinamento pode ocorrer na região estendida da rede.

Algoritmo para treinamento

Step 1 - Inicialize os pesos, a taxa de aprendizagem α e o esquema topológico da vizinhança.

Step 2 - Continue a etapa 3-9, quando a condição de parada não for verdadeira.

Step 3 - Continue a etapa 4-6 para cada vetor de entrada x.

Step 4 - Calcular o quadrado da distância euclidiana para j = 1 to m

$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 5 - Obtenha a unidade vencedora J Onde D(j) é mínimo.

Step 6 - Calcule o novo peso da unidade vencedora pela seguinte relação -

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (antigo)] $$

Step 7 - Atualize a taxa de aprendizagem α pela seguinte relação -

$$ \ alpha (t \: + \: 1) \: = \: 0,5 \ alpha t $$

Step 8 - Reduzir o raio do esquema topológico.

Step 9 - Verifique a condição de parada da rede.

Esses tipos de redes neurais funcionam com base na associação de padrões, o que significa que podem armazenar padrões diferentes e, no momento de fornecer uma saída, podem produzir um dos padrões armazenados, combinando-os com o padrão de entrada fornecido. Esses tipos de memórias também são chamadosContent-Addressable Memory(CAM). A memória associativa faz uma pesquisa paralela com os padrões armazenados como arquivos de dados.

A seguir estão os dois tipos de memórias associativas que podemos observar -

Memória Auto Associativa
Memória heteroassociativa

Memória Auto Associativa

Esta é uma rede neural de camada única na qual o vetor de treinamento de entrada e os vetores de destino de saída são os mesmos. Os pesos são determinados para que a rede armazene um conjunto de padrões.

Arquitetura

Conforme mostrado na figura a seguir, a arquitetura da rede de memória Auto Associativa tem ‘n’ número de vetores de treinamento de entrada e semelhantes ‘n’ número de vetores de destino de saída.

Algoritmo de treinamento

Para treinamento, esta rede está usando a regra de aprendizagem Hebb ou Delta.

Step 1 - Inicialize todos os pesos para zero como w_ij = 0 (i = 1 to n, j = 1 to n)

Step 2 - Execute as etapas 3-4 para cada vetor de entrada.

Step 3 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 4 - Ative cada unidade de saída da seguinte forma -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: para \: n) $$

Step 5 - Ajuste os pesos da seguinte forma -

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: x_ {i} y_ {j} $$

Algoritmo de teste

Step 1 - Defina os pesos obtidos durante o treinamento para a regra de Hebb.

Step 2 - Execute as etapas 3 a 5 para cada vetor de entrada.

Step 3 - Defina a ativação das unidades de entrada igual à do vetor de entrada.

Step 4 - Calcular a entrada líquida para cada unidade de produção j = 1 to n

$$ y_ {inj} \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Aplique a seguinte função de ativação para calcular a saída

$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ - 1 & if \: y_ {inj} \: \ leqslant \: 0 \ end {casos} $$

Memória heteroassociativa

Semelhante à rede de memória autoassociativa, esta também é uma rede neural de camada única. No entanto, nesta rede, o vetor de treinamento de entrada e os vetores de destino de saída não são os mesmos. Os pesos são determinados para que a rede armazene um conjunto de padrões. A rede heteroassociativa é de natureza estática, portanto, não haveria operações não lineares e de atraso.

Arquitetura

Conforme mostrado na figura a seguir, a arquitetura da rede de Memória Hetero Associativa tem ‘n’ número de vetores de treinamento de entrada e ‘m’ número de vetores de destino de saída.

Algoritmo de treinamento

Para treinamento, esta rede está usando a regra de aprendizagem Hebb ou Delta.

Step 1 - Inicialize todos os pesos para zero como w_ij = 0 (i = 1 to n, j = 1 to m)

Step 2 - Execute as etapas 3-4 para cada vetor de entrada.

Step 3 - Ative cada unidade de entrada da seguinte forma -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: para \: n) $$

Step 4 - Ative cada unidade de saída da seguinte forma -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: a \: m) $$

Step 5 - Ajuste os pesos da seguinte forma -

$$ w_ {ij} (novo) \: = \: w_ {ij} (antigo) \: + \: x_ {i} y_ {j} $$

Algoritmo de teste

Step 1 - Defina os pesos obtidos durante o treinamento para a regra de Hebb.

Step 2 - Execute as etapas 3 a 5 para cada vetor de entrada.

Step 3 - Defina a ativação das unidades de entrada igual à do vetor de entrada.

Step 4 - Calcular a entrada líquida para cada unidade de produção j = 1 to m;

$$ y_ {inj} \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Aplique a seguinte função de ativação para calcular a saída

$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ 0 & if \ : y_ {inj} \: = \: 0 \\ - 1 & if \: y_ {inj} \: <\: 0 \ end {cases} $$

A rede neural de Hopfield foi inventada pelo Dr. John J. Hopfield em 1982. Ela consiste em uma única camada que contém um ou mais neurônios recorrentes totalmente conectados. A rede Hopfield é comumente usada para tarefas de autoassociação e otimização.

Discrete Hopfield Network

Uma rede Hopfield que opera em linha discreta ou em outras palavras, pode-se dizer que os padrões de entrada e saída são vetores discretos, que podem ser de natureza binária (0,1) ou bipolar (+1, -1). A rede tem pesos simétricos sem auto-conexões, ou seja,w_ij = w_ji e w_ii = 0.

Arquitetura

A seguir estão alguns pontos importantes para se manter em mente sobre a rede Hopfield discreta -

Este modelo consiste em neurônios com uma saída inversora e uma não inversora.
A saída de cada neurônio deve ser a entrada de outros neurônios, mas não a entrada do próprio.
Peso / força da conexão é representado por w_ij.
As conexões podem ser tanto excitatórias quanto inibitórias. Seria excitatório, se a saída do neurônio fosse igual à entrada, caso contrário, inibitória.
Os pesos devem ser simétricos, ou seja w_ij = w_ji

A saída de Y₁ Indo a Y₂, Y_i e Y_n tem os pesos w₁₂, w_1i e w_1nrespectivamente. Da mesma forma, outros arcos têm os pesos sobre eles.

Algoritmo de treinamento

Durante o treinamento da rede discreta de Hopfield, os pesos serão atualizados. Como sabemos, podemos ter tanto os vetores de entrada binários quanto os vetores de entrada bipolares. Portanto, em ambos os casos, as atualizações de peso podem ser feitas com a seguinte relação

Case 1 - Padrões de entrada binários

Para um conjunto de padrões binários s(p), p = 1 to P

Aqui, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Matriz de peso é dada por

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: para \: i \: \ neq \: j $$

Case 2 - Padrões de entrada bipolar

Para um conjunto de padrões binários s(p), p = 1 to P

Aqui, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Matriz de peso é dada por

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: para \ : i \: \ neq \: j $$

Algoritmo de teste

Step 1 - Inicialize os pesos, que são obtidos do algoritmo de treinamento usando o princípio de Hebbian.

Step 2 - Execute os passos 3 a 9, se as ativações da rede não estiverem consolidadas.

Step 3 - Para cada vetor de entrada X, execute as etapas 4-8.

Step 4 - Faça a ativação inicial da rede igual ao vetor de entrada externa X como segue -

$$ y_ {i} \: = \: x_ {i} \: \: \: para \: i \: = \: 1 \: para \: n $$

Step 5 - Para cada unidade Y_i, execute as etapas 6-9.

Step 6 - Calcule a entrada líquida da rede da seguinte forma -

$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$

Step 7 - Aplique a ativação da seguinte forma sobre a entrada líquida para calcular a saída -

$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {casos} $$

Aqui $ \ theta_ {i} $ é o limite.

Step 8 - Transmita esta saída y_i para todas as outras unidades.

Step 9 - Teste a rede para a conjunção.

Avaliação da função energética

Uma função de energia é definida como uma função ligada e não crescente do estado do sistema.

Função de energia E_f⁡, ⁡ também chamado Lyapunov function determina a estabilidade da rede Hopfield discreta e é caracterizada da seguinte forma -

$$ E_ {f} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ theta_ {i} y_ {i} $$

Condition - Em uma rede estável, sempre que o estado do nó muda, a função de energia acima diminuirá.

Suponha que quando o nó i mudou de estado de $ y_i ^ {(k)} $ para $ y_i ^ {(k \: + \: 1)} $ ⁡então a mudança de energia $ \ Delta E_ {f} $ é dada pela seguinte relação

$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$

$$ = \: - \ left (\ begin {array} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$

$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$

Aqui $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $

A mudança na energia depende do fato de que apenas uma unidade pode atualizar sua ativação por vez.

Rede Hopfield Contínua

Em comparação com a rede discreta de Hopfield, a rede contínua tem o tempo como uma variável contínua. Também é usado em problemas de auto-associação e otimização, como o problema do caixeiro viajante.

Model - O modelo ou arquitetura pode ser construído adicionando componentes elétricos, como amplificadores que podem mapear a tensão de entrada para a tensão de saída através de uma função de ativação sigmóide.

Avaliação da função energética

$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ limits_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$

Aqui λ é o parâmetro de ganho e g_ri condutância de entrada.

Estes são processos de aprendizagem estocásticos com estrutura recorrente e são a base das primeiras técnicas de otimização utilizadas em RNA. A Máquina Boltzmann foi inventada por Geoffrey Hinton e Terry Sejnowski em 1985. Mais clareza pode ser observada nas palavras de Hinton sobre a Máquina Boltzmann.

“Uma característica surpreendente dessa rede é que ela usa apenas informações disponíveis localmente. A mudança de peso depende apenas do comportamento das duas unidades que ele conecta, embora a mudança otimize uma medida global ”- Ackley, Hinton 1985.

Alguns pontos importantes sobre a Máquina Boltzmann -

Eles usam estrutura recorrente.
Eles consistem em neurônios estocásticos, que têm um dos dois estados possíveis, 1 ou 0.
Alguns dos neurônios neste são adaptativos (estado livre) e alguns são presos (estado congelado).
Se aplicarmos o recozimento simulado na rede discreta de Hopfield, ela se tornaria a Máquina de Boltzmann.

Objetivo da Máquina Boltzmann

O objetivo principal da Máquina Boltzmann é otimizar a solução de um problema. É trabalho da Boltzmann Machine otimizar os pesos e as quantidades relacionadas a esse problema específico.

Arquitetura

O diagrama a seguir mostra a arquitetura da máquina Boltzmann. É claro a partir do diagrama, que é uma matriz bidimensional de unidades. Aqui, os pesos nas interconexões entre as unidades são–p Onde p > 0. Os pesos das auto-conexões são dados porb Onde b > 0.

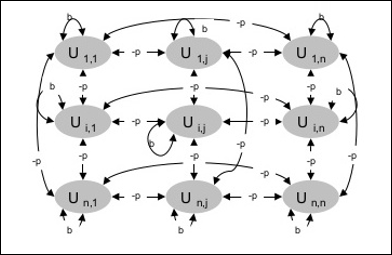
Algoritmo de treinamento

Como sabemos que as máquinas Boltzmann têm pesos fixos, não haverá algoritmo de treinamento, pois não precisamos atualizar os pesos na rede. No entanto, para testar a rede, temos que definir os pesos, bem como encontrar a função de consenso (CF).

A máquina Boltzmann possui um conjunto de unidades U_i e U_j e tem conexões bidirecionais neles.

Estamos considerando o peso fixo, digamos w_ij.
w_ij ≠ 0 E se U_i e U_j estão conectados.
Também existe uma simetria na interconexão ponderada, ou seja, w_ij = w_ji.
w_ii também existe, ou seja, haveria a auto-conexão entre as unidades.
Para qualquer unidade U_i, seu estado u_i seria 1 ou 0.

O objetivo principal da Máquina Boltzmann é maximizar a Função de Consenso (CF) que pode ser dada pela seguinte relação

$$ CF \: = \: \ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

Agora, quando o estado muda de 1 para 0 ou de 0 para 1, então a mudança no consenso pode ser dada pela seguinte relação -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$

Aqui u_i é o estado atual de U_i.

A variação no coeficiente (1 - 2u_i) é dado pela seguinte relação -

$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {cases} +1, & U_ {i} \: is \: atualmente \: off \\ - 1, & U_ {i } \: está \: atualmente \: em \ end {casos} $$

Geralmente, unidade U_inão muda seu estado, mas se o fizer, então as informações estarão residindo no local da unidade. Com essa mudança, também haveria um aumento no consenso da rede.

A probabilidade da rede aceitar a mudança no estado da unidade é dada pela seguinte relação -

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Aqui, Té o parâmetro de controle. Ele diminuirá à medida que CF atinge o valor máximo.

Algoritmo de teste

Step 1 - Inicialize o seguinte para iniciar o treinamento -

Pesos que representam a restrição do problema
Parâmetro de controle T

Step 2 - Continue as etapas 3-8, quando a condição de parada não for verdadeira.

Step 3 - Execute as etapas 4-7.

Step 4 - Suponha que um dos estados alterou o peso e escolha o inteiro I, J como valores aleatórios entre 1 e n.

Step 5 - Calcule a mudança de consenso da seguinte forma -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$

Step 6 - Calcule a probabilidade de que esta rede aceite a mudança de estado

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Step 7 - Aceite ou rejeite esta mudança da seguinte forma -

Case I - se R < AF, aceite a mudança.

Case II - se R ≥ AF, rejeite a mudança.

Aqui, R é o número aleatório entre 0 e 1.

Step 8 - Reduza o parâmetro de controle (temperatura) da seguinte forma -

T(new) = ⁡0.95T(old)

Step 9 - Teste as condições de parada, que podem ser as seguintes -

A temperatura atinge um valor especificado
Não há mudança de estado para um determinado número de iterações

A rede neural Brain-State-in-a-Box (BSB) é uma rede neural auto-associativa não linear e pode ser estendida para hetero-associação com duas ou mais camadas. Também é semelhante à rede Hopfield. Foi proposto por JA Anderson, JW Silverstein, SA Ritz e RS Jones em 1977.

Alguns pontos importantes a serem lembrados sobre a Rede BSB -

É uma rede totalmente conectada com o número máximo de nós dependendo da dimensionalidade n do espaço de entrada.
Todos os neurônios são atualizados simultaneamente.
Os neurônios assumem valores entre -1 e +1.

Formulações Matemáticas

A função de nó usada na rede BSB é uma função de rampa, que pode ser definida da seguinte forma -

$$ f (net) \: = \: min (1, \: max (-1, \: net)) $$

Esta função de rampa é limitada e contínua.

Como sabemos que cada nó mudaria de estado, isso pode ser feito com a ajuda da seguinte relação matemática -

$$ x_ {t} (t \: + \: 1) \: = \: f \ left (\ begin {array} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {i, j } x_ {j} (t) \ end {array} \ right) $$

Aqui, x_i(t) é o estado do i_th nó no tempo t.

Pesos de i_th nó para j_th nó pode ser medido com a seguinte relação -

$$ w_ {ij} \: = \: \ frac {1} {P} \ displaystyle \ sum \ limits_ {p = 1} ^ P (v_ {p, i} \: v_ {p, j}) $$

Aqui, P é o número de padrões de treinamento, que são bipolares.

Otimização é uma ação de tornar algo como design, situação, recurso e sistema o mais eficaz possível. Usando uma semelhança entre a função de custo e a função de energia, podemos usar neurônios altamente interconectados para resolver problemas de otimização. Esse tipo de rede neural é a rede de Hopfield, que consiste em uma única camada contendo um ou mais neurônios recorrentes totalmente conectados. Isso pode ser usado para otimização.

Pontos a serem lembrados ao usar a rede Hopfield para otimização -

A função de energia deve ser mínima da rede.
Ele encontrará uma solução satisfatória em vez de selecionar um dos padrões armazenados.
A qualidade da solução encontrada pela rede Hopfield depende significativamente do estado inicial da rede.

Problema do caixeiro viajante

Encontrar o caminho mais curto percorrido pelo vendedor é um dos problemas computacionais, que pode ser otimizado usando a rede neural de Hopfield.

Conceito Básico de TSP

O Problema do Caixeiro Viajante (TSP) é um problema clássico de otimização em que um vendedor tem que viajar ncidades, que estão conectadas entre si, mantendo o custo e a distância percorrida mínimos. Por exemplo, o vendedor tem que percorrer um conjunto de 4 cidades A, B, C, D e o objetivo é encontrar o trajeto circular mais curto, ABC-D, de forma a minimizar o custo, que inclui também o custo da viagem de a última cidade D para a primeira cidade A.

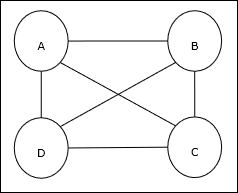
Representação de Matriz

Na verdade, cada passeio do TSP de n-cidades pode ser expresso como n × n matriz de quem i_th linha descreve o i_thlocalização da cidade. Esta matriz,M, para 4 cidades A, B, C, D pode ser expresso da seguinte forma -

$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 e 0 e 1 \ end {bmatrix} $$

Solução da Hopfield Network

Considerando a solução deste TSP pela rede Hopfield, cada nó da rede corresponde a um elemento da matriz.

Cálculo da função de energia

Para ser a solução otimizada, a função de energia deve ser mínima. Com base nas seguintes restrições, podemos calcular a função de energia da seguinte forma -

Restrição-I

A primeira restrição, com base na qual calcularemos a função de energia, é que um elemento deve ser igual a 1 em cada linha da matriz M e outros elementos em cada linha devem ser iguais a 0porque cada cidade pode ocorrer em apenas uma posição no tour do TSP. Esta restrição pode ser matematicamente escrita da seguinte forma -

$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: para \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Agora, a função de energia a ser minimizada, com base na restrição acima, conterá um termo proporcional a -

$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

Restrição-II

Como sabemos, no TSP uma cidade pode ocorrer em qualquer posição no passeio, portanto, em cada coluna da matriz M, um elemento deve ser igual a 1 e os outros elementos devem ser iguais a 0. Esta restrição pode ser matematicamente escrita da seguinte maneira -

$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: para \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Agora, a função de energia a ser minimizada, com base na restrição acima, conterá um termo proporcional a -

$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

Cálculo da Função de Custo

Vamos supor uma matriz quadrada de (n × n) denotado por C denota a matriz de custo do TSP para n cidades onde n > 0. A seguir estão alguns parâmetros ao calcular a função de custo -

C_{x, y} - O elemento da matriz de custo denota o custo de viajar da cidade x para y.
A adjacência dos elementos de A e B pode ser mostrada pela seguinte relação -

$$ M_ {x, i} \: = \: 1 \: \: e \: \: M_ {y, i \ pm 1} \: = \: 1 $$

Como sabemos, em Matrix, o valor de saída de cada nó pode ser 0 ou 1, portanto, para cada par de cidades A, B, podemos adicionar os seguintes termos à função de energia -

$$ \ displaystyle \ sum \ limits_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$

Com base na função de custo acima e no valor de restrição, a função de energia final E pode ser dado da seguinte forma -

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$

$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$

Aqui, γ₁ e γ₂ são duas constantes de pesagem.

Técnica de gradiente descendente iterado

A descida gradiente, também conhecida como descida mais íngreme, é um algoritmo de otimização iterativa para encontrar um mínimo local de uma função. Enquanto minimizamos a função, estamos preocupados com o custo ou erro a ser minimizado (Lembre-se do problema do caixeiro viajante). É amplamente utilizado no aprendizado profundo, o que é útil em uma ampla variedade de situações. O ponto a ser lembrado é que nos preocupamos com a otimização local e não com a otimização global.

Ideia Principal de Trabalho

Podemos entender a ideia principal de trabalho da descida de gradiente com a ajuda das seguintes etapas -

Primeiro, comece com uma estimativa inicial da solução.
Então, pegue o gradiente da função nesse ponto.
Mais tarde, repita o processo avançando a solução na direção negativa do gradiente.

Seguindo as etapas acima, o algoritmo eventualmente convergirá onde o gradiente é zero.

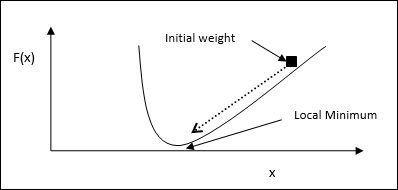
Conceito Matemático

Suponha que temos uma função f(x)e estamos tentando encontrar o mínimo dessa função. A seguir estão as etapas para encontrar o mínimo def(x).

Primeiro, dê algum valor inicial $ x_ {0} \: for \: x $
Agora pegue o gradiente $ \ nabla f $ ⁡ da função, com a intuição de que o gradiente dará a inclinação da curva naquele x e sua direção apontará para o aumento da função, para descobrir a melhor direção para minimizá-la.
Agora mude x da seguinte forma -

$$ x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n}) $$

Aqui, θ > 0 é a taxa de treinamento (tamanho do passo) que força o algoritmo a dar pequenos saltos.

Estimando o tamanho do passo

Na verdade, um tamanho de passo errado θpode não atingir a convergência, portanto, uma seleção cuidadosa do mesmo é muito importante. Os seguintes pontos devem ser lembrados ao escolher o tamanho do passo

Não escolha um tamanho de passo muito grande, caso contrário, terá um impacto negativo, ou seja, irá divergir ao invés de convergir.
Não escolha um tamanho de passo muito pequeno, caso contrário, demorará muito para convergir.

Algumas opções com relação à escolha do tamanho do passo -

Uma opção é escolher um tamanho de passo fixo.
Outra opção é escolher um tamanho de etapa diferente para cada iteração.

Recozimento simulado

O conceito básico de Simulated Annealing (SA) é motivado pelo recozimento em sólidos. No processo de recozimento, se aquecermos um metal acima de seu ponto de fusão e resfriá-lo, as propriedades estruturais dependerão da taxa de resfriamento. Também podemos dizer que SA simula o processo metalúrgico de recozimento.

Use em ANN

SA é um método computacional estocástico, inspirado na analogia do Annealing, para aproximar a otimização global de uma dada função. Podemos usar SA para treinar redes neurais feed-forward.

Algoritmo

Step 1 - Gere uma solução aleatória.

Step 2 - Calcule seu custo usando alguma função de custo.

Step 3 - Gere uma solução vizinha aleatória.

Step 4 - Calcular o custo da nova solução pela mesma função de custo.

Step 5 - Compare o custo de uma nova solução com o de uma solução antiga da seguinte forma -

E se Cost_{New Solution} < Cost_{Old Solution} em seguida, passe para a nova solução.

Step 6 - Teste a condição de parada, que pode ser o número máximo de iterações alcançadas ou obter uma solução aceitável.

A natureza sempre foi uma grande fonte de inspiração para toda a humanidade. Algoritmos Genéticos (AGs) são algoritmos baseados em pesquisa baseados nos conceitos de seleção natural e genética. GAs são um subconjunto de um ramo muito maior de computação conhecido comoEvolutionary Computation.

GAs foi desenvolvido por John Holland e seus alunos e colegas da Universidade de Michigan, principalmente David E. Goldberg, e desde então foi testado em vários problemas de otimização com um alto grau de sucesso.

Em AGs, temos um conjunto ou população de soluções possíveis para o problema em questão. Essas soluções então passam por recombinação e mutação (como na genética natural), produzindo novos filhos, e o processo se repete por várias gerações. Cada indivíduo (ou solução candidata) recebe um valor de aptidão (com base em seu valor de função objetivo) e os indivíduos mais aptos têm uma chance maior de acasalar e produzir indivíduos mais "aptos". Isso está de acordo com a teoria darwiniana de “sobrevivência do mais apto”.

Dessa forma, continuamos “evoluindo” melhores indivíduos ou soluções ao longo das gerações, até chegarmos a um critério de parada.

Algoritmos genéticos são suficientemente aleatórios por natureza, no entanto, eles têm um desempenho muito melhor do que a pesquisa local aleatória (na qual apenas tentamos várias soluções aleatórias, mantendo o controle das melhores até agora), pois eles exploram informações históricas também.

Vantagens dos GAs

Os AGs têm várias vantagens que os tornaram imensamente populares. Isso inclui -

Não requer nenhuma informação derivada (que pode não estar disponível para muitos problemas do mundo real).
É mais rápido e eficiente em comparação com os métodos tradicionais.
Possui recursos paralelos muito bons.
Otimiza funções contínuas e discretas, bem como problemas multi-objetivos.
Fornece uma lista de soluções “boas” e não apenas uma solução única.
Sempre obtém uma resposta para o problema, que fica melhor com o tempo.
Útil quando o espaço de pesquisa é muito grande e há um grande número de parâmetros envolvidos.

Limitações de GAs

Como qualquer técnica, os AGs também sofrem de algumas limitações. Isso inclui -

Os AGs não são adequados para todos os problemas, especialmente problemas que são simples e para os quais informações derivadas estão disponíveis.
O valor de aptidão é calculado repetidamente, o que pode ser caro do ponto de vista computacional para alguns problemas.
Por ser estocástico, não há garantias sobre a otimalidade ou a qualidade da solução.
Se não for implementado corretamente, o GA pode não convergir para a solução ideal.

GA - Motivação

Algoritmos genéticos têm a capacidade de fornecer uma solução “boa o suficiente” “rápida o suficiente”. Isso torna o gás atraente para uso na solução de problemas de otimização. Os motivos pelos quais os AGs são necessários são os seguintes -

Resolvendo problemas difíceis

Na ciência da computação, há um grande conjunto de problemas, que são NP-Hard. O que isso significa essencialmente é que, mesmo os sistemas de computação mais poderosos levam muito tempo (até anos!) Para resolver esse problema. Em tal cenário, GAs provam ser uma ferramenta eficiente para fornecerusable near-optimal solutions em um curto espaço de tempo.

Falha de métodos baseados em gradiente

Os métodos tradicionais baseados em cálculo funcionam começando em um ponto aleatório e movendo-se na direção do gradiente, até chegarmos ao topo da colina. Essa técnica é eficiente e funciona muito bem para funções objetivo de pico único, como a função de custo na regressão linear. No entanto, na maioria das situações do mundo real, temos um problema muito complexo chamado de paisagens, feito de muitos picos e muitos vales, que faz com que tais métodos falhem, pois sofrem de uma tendência inerente de ficarem presos nos ótimos locais, conforme mostrado na figura a seguir.

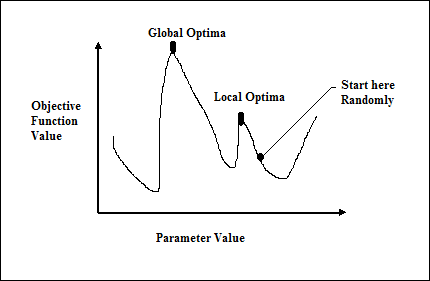
Obtendo uma boa solução rapidamente

Alguns problemas difíceis, como o Travelling Salesman Problem (TSP), têm aplicações do mundo real, como localização de caminhos e projeto VLSI. Agora imagine que você está usando seu sistema de navegação GPS e leva alguns minutos (ou mesmo algumas horas) para calcular o caminho “ótimo” da origem ao destino. Atrasos em tais aplicativos do mundo real não são aceitáveis e, portanto, uma solução “boa o suficiente”, que é entregue “rápido” é o que é necessário.

Como usar o GA para problemas de otimização?

Já sabemos que otimização é uma ação de tornar algo como design, situação, recurso e sistema o mais eficaz possível. O processo de otimização é mostrado no diagrama a seguir.

Estágios do mecanismo de GA para o processo de otimização

A seguir estão os estágios do mecanismo de GA quando usados para otimização de problemas.

Gere a população inicial aleatoriamente.
Selecione a solução inicial com os melhores valores de fitness.
Recombine as soluções selecionadas usando operadores de mutação e crossover.
Insira a prole na população.
Agora, se a condição de parada for atendida, retorne a solução com seu melhor valor de adequação. Caso contrário, vá para a etapa 2.

Antes de estudar os campos onde a RNA tem sido usada extensivamente, precisamos entender por que a RNA seria a escolha preferencial de aplicação.

Por que redes neurais artificiais?

Precisamos entender a resposta à pergunta acima com um exemplo de ser humano. Quando crianças, aprendíamos as coisas com a ajuda dos mais velhos, o que inclui nossos pais ou professores. Então, mais tarde, por autoaprendizagem ou prática, continuamos aprendendo por toda a vida. Cientistas e pesquisadores também estão tornando a máquina inteligente, assim como um ser humano, e a RNA desempenha um papel muito importante no mesmo devido às seguintes razões -

Com a ajuda de redes neurais, podemos encontrar a solução de tais problemas para os quais o método algorítmico é caro ou não existe.
As redes neurais podem aprender por exemplo, portanto, não precisamos programá-lo muito.
As redes neurais têm a precisão e velocidade significativamente mais rápida do que a velocidade convencional.

Areas de aplicação

A seguir estão algumas das áreas onde a RNA está sendo usada. Isso sugere que a RNA tem uma abordagem interdisciplinar em seu desenvolvimento e aplicações.

Reconhecimento de fala

A fala ocupa um papel proeminente na interação humano-humano. Portanto, é natural que as pessoas esperem interfaces de fala com computadores. Na era atual, para se comunicar com as máquinas, os humanos ainda precisam de linguagens sofisticadas, difíceis de aprender e usar. Para amenizar essa barreira de comunicação, uma solução simples poderia ser a comunicação em um idioma falado que seja possível para a máquina entender.

Grande progresso foi feito neste campo, no entanto, esses tipos de sistemas ainda estão enfrentando o problema de vocabulário ou gramática limitada, juntamente com a questão do retreinamento do sistema para diferentes falantes em diferentes condições. ANN está desempenhando um papel importante nesta área. As seguintes RNAs foram utilizadas para reconhecimento de voz -

Redes multicamadas
Redes multicamadas com conexões recorrentes
Mapa de recursos auto-organizáveis de Kohonen

A rede mais útil para isso é o mapa de recursos de auto-organização Kohonen, que tem sua entrada como segmentos curtos da forma de onda da fala. Ele mapeará o mesmo tipo de fonema do array de saída, chamado de técnica de extração de recurso. Após extrair os traços, com a ajuda de alguns modelos acústicos como processamento back-end, ele reconhecerá o enunciado.

Reconhecimento de Personagem

É um problema interessante que se enquadra na área geral de reconhecimento de padrões. Muitas redes neurais foram desenvolvidas para reconhecimento automático de caracteres escritos à mão, sejam letras ou dígitos. A seguir estão algumas RNAs que têm sido usadas para reconhecimento de caracteres -

Redes neurais multicamadas, como redes neurais de retropropagação.
Neocognitron

Embora as redes neurais de retropropagação tenham várias camadas ocultas, o padrão de conexão de uma camada para a próxima é localizado. Da mesma forma, o neocognitron também possui várias camadas ocultas e seu treinamento é feito camada por camada para este tipo de aplicações.

Solicitação de verificação de assinatura

As assinaturas são uma das formas mais úteis de autorizar e autenticar uma pessoa em transações jurídicas. A técnica de verificação de assinatura é uma técnica não baseada em visão.

Para esta aplicação, a primeira abordagem é extrair o recurso, ou melhor, o conjunto de recursos geométricos que representa a assinatura. Com esses conjuntos de recursos, temos que treinar as redes neurais usando um algoritmo de rede neural eficiente. Essa rede neural treinada classificará a assinatura como genuína ou forjada no estágio de verificação.

Reconhecimento de Face Humana

É um dos métodos biométricos para identificar uma determinada face. É uma tarefa típica devido à caracterização de imagens “não faciais”. No entanto, se uma rede neural for bem treinada, ela pode ser dividida em duas classes, a saber: imagens com rostos e imagens que não têm rostos.

Primeiro, todas as imagens de entrada devem ser pré-processadas. Então, a dimensionalidade dessa imagem deve ser reduzida. E, finalmente, deve ser classificado usando o algoritmo de treinamento de rede neural. As seguintes redes neurais são usadas para fins de treinamento com imagem pré-processada -

Rede neural de feed-forward multicamadas totalmente conectada treinada com a ajuda do algoritmo de propagação reversa
Para a redução da dimensionalidade, é usada a Análise de Componentes Principais (PCA).