Aprendizagem e Adaptação
Como afirmado anteriormente, a RNA é completamente inspirada pela maneira como o sistema nervoso biológico, ou seja, o cérebro humano funciona. A característica mais impressionante do cérebro humano é aprender, portanto, a mesma característica é adquirida pela RNA.
O que está aprendendo na ANN?
Basicamente, aprender significa fazer e adaptar a mudança em si, conforme e quando há uma mudança no ambiente. A RNA é um sistema complexo ou mais precisamente podemos dizer que é um sistema adaptativo complexo, que pode mudar sua estrutura interna com base na informação que passa por ele.
Por que isso é importante?
Por ser um sistema adaptativo complexo, o aprendizado em RNA implica que uma unidade de processamento é capaz de alterar seu comportamento de entrada / saída devido à mudança no ambiente. A importância do aprendizado em RNA aumenta por causa da função de ativação fixa, bem como do vetor de entrada / saída, quando uma rede particular é construída. Agora, para alterar o comportamento de entrada / saída, precisamos ajustar os pesos.
Classificação
Pode ser definido como o processo de aprender a distinguir os dados de amostras em classes diferentes, encontrando características comuns entre as amostras das mesmas classes. Por exemplo, para realizar o treinamento de RNA, temos alguns exemplos de treinamento com recursos exclusivos, e para realizar seus testes, temos alguns exemplos de teste com outros recursos exclusivos. A classificação é um exemplo de aprendizagem supervisionada.
Regras de aprendizagem de rede neural
Sabemos que, durante o aprendizado da RNA, para alterar o comportamento de entrada / saída, precisamos ajustar os pesos. Portanto, é necessário um método com o qual os pesos possam ser modificados. Esses métodos são chamados de regras de aprendizagem, que são simplesmente algoritmos ou equações. A seguir estão algumas regras de aprendizagem para a rede neural -
Regra de Aprendizagem Hebbian
Essa regra, uma das mais antigas e simples, foi introduzida por Donald Hebb em seu livro The Organization of Behavior, em 1949. É uma espécie de aprendizagem direta e não supervisionada.
Basic Concept - Esta regra é baseada em uma proposta dada por Hebb, que escreveu -
“Quando um axônio da célula A está perto o suficiente para excitar uma célula B e repetidamente ou persistentemente participa de seu disparo, algum processo de crescimento ou alteração metabólica ocorre em uma ou em ambas as células, de forma que a eficiência de A, como uma das células disparando B , Está melhorado."
A partir do postulado acima, podemos concluir que as conexões entre dois neurônios podem ser fortalecidas se os neurônios dispararem ao mesmo tempo e podem enfraquecer se dispararem em momentos diferentes.
Mathematical Formulation - De acordo com a regra de aprendizagem Hebbian, segue a fórmula para aumentar o peso da conexão a cada passo de tempo.
$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$
Aqui, $ \ Delta w_ {ji} (t) $ = incremento pelo qual o peso da conexão aumenta no intervalo de tempo t
$ \ alpha $ = a taxa de aprendizagem positiva e constante
$ x_ {i} (t) $ = o valor de entrada do neurônio pré-sináptico no intervalo de tempo t
$ y_ {i} (t) $ = a saída do neurônio pré-sináptico na mesma etapa de tempo t
Regra de aprendizagem do Perceptron
Esta regra é um erro que corrige o algoritmo de aprendizado supervisionado de redes feedforward de camada única com função de ativação linear, introduzido por Rosenblatt.
Basic Concept- Por ser supervisionado por natureza, para calcular o erro, haveria uma comparação entre a saída desejada / alvo e a saída real. Se houver alguma diferença encontrada, então uma mudança deve ser feita nos pesos da conexão.
Mathematical Formulation - Para explicar sua formulação matemática, suponha que temos 'n' número de vetores de entrada finitos, x (n), junto com seu vetor de saída desejado / alvo t (n), onde n = 1 a N.
Agora, a saída 'y' pode ser calculada, conforme explicado anteriormente com base na entrada líquida, e a função de ativação aplicada sobre essa entrada líquida pode ser expressa da seguinte forma -
$$ y \: = \: f (y_ {in}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {casos} $$
Onde θ é o limiar.
A atualização do peso pode ser feita nos dois casos seguintes -
Case I - quando t ≠ y, então
$$ w (novo) \: = \: w (antigo) \: + \; tx $$
Case II - quando t = y, então
Sem mudança de peso
Regra de aprendizagem Delta (regra de Widrow-Hoff)
É introduzido por Bernard Widrow e Marcian Hoff, também chamado de método Least Mean Square (LMS), para minimizar o erro em todos os padrões de treinamento. É uma espécie de algoritmo de aprendizado supervisionado com função de ativação contínua.
Basic Concept- A base desta regra é a abordagem gradiente-descendente, que continua para sempre. A regra delta atualiza os pesos sinápticos de modo a minimizar a entrada líquida para a unidade de saída e o valor de destino.
Mathematical Formulation - Para atualizar os pesos sinápticos, a regra delta é dada por
$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$
Aqui $ \ Delta W_ {i} $ = mudança de peso para o i th pattern;
$ \ alpha $ = a taxa de aprendizagem positiva e constante;
$ x_ {i} $ = o valor de entrada do neurônio pré-sináptico;
$ e_ {j} $ = $ (t \: - \: y_ {in}) $, a diferença entre a saída desejada / alvo e a saída real $ y_ {in} $
A regra delta acima é para uma única unidade de saída apenas.
A atualização do peso pode ser feita nos dois casos seguintes -
Case-I - quando t ≠ y, então
$$ w (novo) \: = \: w (antigo) \: + \: \ Delta w $$
Case-II - quando t = y, então
Sem mudança de peso
Regra de aprendizagem competitiva (o vencedor leva tudo)
Ele está relacionado ao treinamento não supervisionado no qual os nós de saída tentam competir entre si para representar o padrão de entrada. Para entender esta regra de aprendizagem, devemos entender a rede competitiva que é dada a seguir -
Basic Concept of Competitive Network- Esta rede é como uma rede feedforward de camada única com conexão de feedback entre as saídas. As conexões entre as saídas são do tipo inibidoras, representadas por linhas pontilhadas, o que significa que os concorrentes nunca se sustentam.
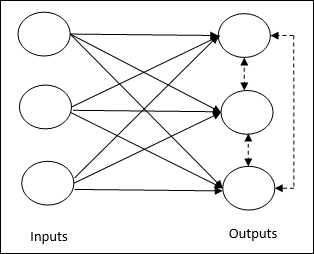
Basic Concept of Competitive Learning Rule- Como dito anteriormente, haverá uma competição entre os nós de saída. Portanto, o conceito principal é que durante o treinamento, a unidade de saída com a maior ativação para um determinado padrão de entrada será declarada a vencedora. Essa regra também é chamada de O vencedor leva tudo porque apenas o neurônio vencedor é atualizado e o restante dos neurônios são deixados inalterados.
Mathematical formulation - A seguir estão os três fatores importantes para a formulação matemática desta regra de aprendizagem -
Condition to be a winner - Suponha que se um neurônio $ y_ {k} $ quisesse ser o vencedor, haveria a seguinte condição -
$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & caso contrário \ end {casos} $$
Isso significa que se qualquer neurônio, digamos $ y_ {k} $ , quiser vencer, então seu campo local induzido (a saída da unidade de soma), digamos $ v_ {k} $, deve ser o maior entre todos os outros neurônios na rede.
Condition of sum total of weight - Outra restrição sobre a regra de aprendizagem competitiva é que a soma total dos pesos para um determinado neurônio de saída será 1. Por exemplo, se considerarmos o neurônio k então -
$$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: \: para \: all \: k $$
Change of weight for winner- Se um neurônio não responde ao padrão de entrada, então nenhum aprendizado ocorre naquele neurônio. No entanto, se um determinado neurônio vencer, os pesos correspondentes serão ajustados da seguinte forma
$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & se \: neurônio \: k \: perdas \ end {casos} $$
Aqui $ \ alpha $ é a taxa de aprendizagem.
Isso mostra claramente que estamos favorecendo o neurônio vencedor ajustando seu peso e, se houver uma perda de neurônio, não precisamos nos preocupar em reajustar seu peso.
Regra de Aprendizagem Outstar
Essa regra, introduzida por Grossberg, está preocupada com o aprendizado supervisionado porque os resultados desejados são conhecidos. É também chamado de aprendizagem de Grossberg.
Basic Concept- Esta regra é aplicada sobre os neurônios dispostos em uma camada. É especialmente projetado para produzir uma saída desejadad da camada de p neurônios.
Mathematical Formulation - Os ajustes de peso nesta regra são calculados da seguinte forma
$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$
Aqui d é a saída de neurônio desejada e $ \ alpha $ é a taxa de aprendizado.