Álgebra booleana

A Álgebra Booleana é usada para analisar e simplificar os circuitos digitais (lógicos). Ele usa apenas os números binários, ou seja, 0 e 1. Também é chamado deBinary Algebra ou logical Algebra. A álgebra booleana foi inventada porGeorge Boole em 1854.

Regra em Álgebra Booleana

A seguir estão as regras importantes usadas na álgebra booleana.

• A variável usada pode ter apenas dois valores. Binário 1 para HIGH e Binário 0 para LOW.

• O complemento de uma variável é representado por uma barra superior (-). Assim, o complemento da variável B é representado como

  
  . Assim, se B = 0, então
  
  = 1 e B = 1, então
  
  = 0.

• O OR das variáveis ​​é representado por um sinal de mais (+) entre elas. Por exemplo, ORing de A, B, C é representado como A + B + C.

• O AND lógico de duas ou mais variáveis ​​é representado escrevendo um ponto entre elas, como ABC. Às vezes, o ponto pode ser omitido como ABC.

Leis Booleanas

Existem seis tipos de Leis Booleanas.

Lei comutativa

Qualquer operação binária que satisfaça a seguinte expressão é chamada de operação comutativa.

A lei comutativa afirma que a alteração da sequência das variáveis ​​não tem nenhum efeito na saída de um circuito lógico.

Lei associativa

Esta lei estabelece que a ordem em que as operações lógicas são realizadas é irrelevante, pois seu efeito é o mesmo.

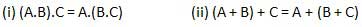
Lei distributiva

A lei distributiva estabelece a seguinte condição.

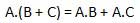
E lei

Essas leis usam a operação AND. Portanto, eles são chamados deAND leis.

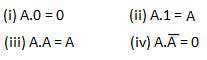
OR lei

Essas leis usam a operação OR. Portanto, eles são chamados deOR leis.

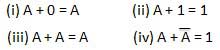
Lei de INVERSÃO

Esta lei usa a operação NOT. A lei da inversão afirma que a dupla inversão de uma variável resulta na própria variável original.

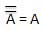
Teoremas Booleanos Importantes

A seguir estão alguns teoremas booleanos importantes.

Função / teoremas booleanos	Descrição
Funções Booleanas	Funções e expressões booleanas, realização de K-Map e NAND Gates
Teoremas de De Morgan	Teorema 1 e Teorema 2 de De Morgan